
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множественная и частная корреляцияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1, чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:
При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции. Отсюда ясно, что, сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора. Можно воспользоваться следующей формулой индекса множественной корреляции:
При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:
Величина множественного коэффициента корреляции зависит не только от корреляции резальтата с каждым из факторов, но и от межфакторной корреляции:
Рассмотренная формула позволяет определить совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов
Поскольку
Ранжирование факторов, участвующих в множественной линейной регрессии, может быть проведено с помощью частных коэффициентов корреляции. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции. Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель. В общем виде при наличии р факторов для уравнения y=a+b1x1+b2x2+ … +bpxp+ε коэффициент частной корреляции, измеряющий влияние на у фактора хiпри неизменном уровне других факторов, можно определить по формуле
При i=1 формула коэффициента частной корреляции примет вид:
Данный коэффициент частной корреляции позволяет измерить тесноту связи между у и хi при неизменном уровне всех других факторов, включенных в уравнение регрессии. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по формуле
Например, для двух факторов формула примет вид:
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1012; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 , где
, где  - общая дисперсия результативного признака;
- общая дисперсия результативного признака; - остаточная дисперсия для уравнения у = f(x1,x2, …,xp).
- остаточная дисперсия для уравнения у = f(x1,x2, …,xp).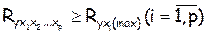 .
.
 , где
, где  - стандартизованные коэффициенты регрессии
- стандартизованные коэффициенты регрессии - парные коэффициенты корреляции результата с каждым фактором.
- парные коэффициенты корреляции результата с каждым фактором.
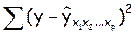 делится на число степеней свободы остаточной вариации (n-m-1), а общая сумма квадратов отклонения
делится на число степеней свободы остаточной вариации (n-m-1), а общая сумма квадратов отклонения  - на число степеней свободы в целом по совокупности (n-1).
- на число степеней свободы в целом по совокупности (n-1).
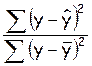 =1-R2, то
=1-R2, то 
 ,
, - множественный коэффициент детерминации всего комплекса р факторов с результатом;
- множественный коэффициент детерминации всего комплекса р факторов с результатом; - тот же показатель детерминации, но без введения в модель фактора хр.
- тот же показатель детерминации, но без введения в модель фактора хр. .
.
 (для i = 1),
(для i = 1), (для i = 2).
(для i = 2).


