
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка значимости частных коэффициентов корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте (при уровне значимости применяемого статистического критерия α= 0,05) Проверяемые гипотезы:
Наблюдаемые значения статистики критерия:
Нахождение tкр - критического значения области отвержения гипотезы Способы: Ø или из статистической таблицы 2 (Значения функции
Ø или с помощью статистической функции Microsoft Excel СТЬЮДРАСПОБР (вероятность; степени_свободы): tкр = СТЬЮДРАСПОБР (α; n-3 ). В данном случае tкр=2,201. Условие отвержения гипотезы о незначимости частного коэффициента корреляции
Результаты проверки гипотез: v гипотеза H0: ρxy/z =0 не отвергается, частный коэффициент корреляции между X и Y не значим; v гипотеза H0: ρxz/y=0 отвергается, частный коэффициент корреляции между X и Z значим; v гипотеза H0: ρyz/x=0 отвергается, частный коэффициент корреляции между Y и Z значим. Интервальные оценки частных коэффициентов корреляции (с надежностью доверительных интервалов γ=0,95) ► Прямое преобразование Фишера выборочных частных коэффициентов корреляции Способы: Ø или с помощью статистической таблицы 6 (Z-преобразования Фишера), Ø или используя встроенную статистическую функцию Microsoft Excel ФИШЕР(x), где x - числовое значение, которое требуется преобразовать. Для исходной выборки
► Определение tγ - квантили уровня (1+γ)/2 распределения Ν(0,1) Способы: Ø или из статистической таблицы 1 (Значения функции Лапласа
Ø или с помощью встроенной статистической функции Microsoft Excel НОРМСТОБР (вероятность), определяющей по уровню (1+γ)/2 значение соответствующей квантили: tγ = НОРМСТОБР ((1+γ)/2). Для заданной надежности tγ=1,96. ► Нахождение границ доверительных интервалов для математических ожиданий Отправное неравенство: Результаты вычислений сведены в таблицу:
► Установление границ доверительных интервалов для частных коэффициентов корреляции ρxy/z, ρxz/y, ρyz/x - обратное преобразование Фишера границ доверительных интервалов для M{arcth(rxy/z)}, M{arcth(rxz/y)}, M{arcth(ryz/x)} Способы: Ø или с помощью статистической таблицы 6 (Z-преобразования Фишера), Ø или используя статистическую функцию Microsoft Excel ФИШЕРОБР(y), где y -значение, для которого совершается обратное преобразование. Отправное неравенство:
Отсюда th(-0,8808)= -0,707< ρxy/z <0,3441 =th(0,3587); th(-1,2623)= -0,852< ρxz/y <-0,023 =th(-0,0228); th(-1,2803)= -0,857< ρyz/x <-0,041 =th(-0,0407). Вывод Доверительные интервалы для частных коэффициентов корреляции ρxz/y, ρyz/x не содержат нуля, что дополнительно подтверждает значимость этих коэффициентов. Сопоставление частных и парных коэффициентов корреляции Исходные статистические данные указывают на то, что между признаками X, Z и между Y, Z имеется существенная обратная умеренная корреляционная зависимость. Влияние третьей переменной (Y, соответственно X) приводит к усилению зависимости между отмеченными случайными величинами, не изменяя направления их связи. Исследование множественных коэффициентов корреляции Условие парной независимости признаков X, Y, Z есть необходимое, но не достаточное условие для обеспечения стохастической независимости этих случайных величин в совокупности, а именно, нулевые значения всех парных коэффициентов корреляции различных переменных данной совокупности не служат в общем случае основанием для вывода об их независимости в целом, что приводит к необходимости использования при корреляционном анализе помимо парных и частных коэффициентов корреляции также множественных коэффициентов корреляции. Множественный коэффициент корреляции между каким-либо показателем (признаком объекта), включенным в анализ, и двумя другими показателями из числа рассматриваемых есть неотрицательная числовая характеристика силы взаимосвязи между данным показателем и совокупностью остальных показателей.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1058; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |




 , где случайная величина T распределена по закону Стьюдента с числом степеней свободы, равным ν) на основании уравнения:
, где случайная величина T распределена по закону Стьюдента с числом степеней свободы, равным ν) на основании уравнения: ,
,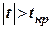
 , где Т имеет стандартное нормальное распределение), исходя из соотношения:
, где Т имеет стандартное нормальное распределение), исходя из соотношения: ,
,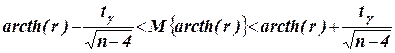 .
.

 .
.


