
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проанализировать линейные коэффициенты парной и частной корреляции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл. 4. С помощью F - критерия Фишера оценить статистическую надежность уравнения регрессии и 5. С помощью частных F - критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1. 6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.
Методические рекомендации и выполнение 1.Для оценки показателей вариации каждого признака необходимо найти где Таблица 10
Продолжение таблицы 10
Сравнивая значения средних квадратических отклонений и средних величин, определим коэффициенты вариации:
Приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%. Совокупность предприятий однородна и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез. Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги: 1)введите исходные данные или откройте существующий файл, содержащий анализируемые данные; 2) в главном меню выберите пункты Сервис/ Анализ данных/Описательная статистика, после чего щелкните по кнопке ОК;
Рис.14 Диалоговое окно ввода параметров инструмента Описательная статистика 3) заполните диалоговое окно ввода данных и параметров вывода (рис. 14): Входной интервал – диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов); Группирование – по столбцам или по строкам – необходимо указать дополнительно; Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Новый рабочий лист – можно задать произвольное имя нового листа. Если необходимо получить дополнительную информацию Итоговой статистики, Уровня надежности, k-го наибольшего и наименьшего значений, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК. Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 15.
Рис. 15. Результат применения инструмента Описательная статистика
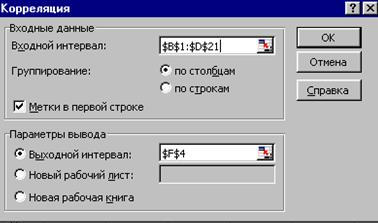
2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого: 1) в главном меню последовательно выберите пункты Сервис/Анализ данных/ Корреляция. Щелкните по кнопке ОК; 2) заполните диалоговое окно ввода данных и параметров вывода (см. рис.16); 3) результаты вычислений – матрица коэффициентов парной корреляции – представлены на рис. 17
Рис.16. Диалоговое окно ввода параметров инструмента Корреляция
Рис.17. Матрица коэффициентов парной корреляции
К сожалению, в ППП MS Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Линейные коэффициенты частной корреляции рассчитаем по рекуррентной формуле:
Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки у как с коэффициентом обновления основных фондов – х1, так и с долей рабочих высокой квалификации – х2(r Коэффициент частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно связаны у и х1: r Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи: r Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи. 3. Вычисление параметров линейного уравнения множественной регрессии проводится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии, описанной в лабораторной работе №1, только в отличие от парной регрессии в диалоговом окне при заполнении параметра входной интервал Х следует указать не один столбец, а все столбцы, содержащие значения факторных признаков: 1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис/Надстройки. Установите флажок Пакет анализа 2) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК (рис.18).
Рис. 18. Диалоговое окно Анализ данных 3) заполните диалоговое окно ввода данных и параметров вывода (рис.19):
Рис.19. Диалоговое окно ввода параметров инструмента Регрессия Входной интервал Y – диапазон, содержащий данные результативного признака Входной интервал Х – диапазон, содержащий данные факторов независимого признака Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет; Константа – ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Новый рабочий лист – можно задать произвольное имя нового листа. Если необходимо получить информацию и графики остатков, установите соответствующие флажки диалоговом окне. Щелкните по кнопке ОК. Результаты анализа представлены на рис. 20.
Рис.20. Результат применения инструмента Регрессия По результатам вычислений составим уравнение множественной регрессии: Значения случайных ошибок параметров b0, b1 и b2 с учетом округления:
Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента: Если значения t – критерия больше 2 – 3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются b0 и b1, а величина b2 сформировалась под воздействием случайных причин, поэтому фактор х2, силу влияния которого оценивает b2, можно исключить как несущественно влияющий, неинформативный. На это же указывает показатель вероятности случайных значений параметров регрессии: если Величина b0 оценивает агрегированное влияние прочих (кроме учтенных в модели факторов х1 и х2) факторов на результат y. Величины b1 и b2 указывают, что с увеличением х1 и х2 на единицу их значений результат увеличивается соответственно на 0,9459 и на 0,0856 млн руб. Сравнивать эти значения не следует, так как они зависят от единиц измерения каждого признака и потому несопоставимы между собой. 4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи По данным таблиц дисперсионного анализа, представленным на рис. 20 Fфакт = 151,65. Вероятность случайно получить такое значение F – критерия составляет 0,0000, что не превышает допустимый уровень значимости 5%; об этом свидетельствует величина P – значения из этих же таблиц. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т. е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 20 в рамках регрессионной статистики. Нескорректированный коэффициент множественной детерминации Скорректированный коэффициент множественной детерминации 5. Найдем частные F критерии для оценки целесообразности включения в модель фактора х1 после фактора х2 и фактора х2после фактора х1:
Частный F-критерий - F F Если поменять первоначальный порядок включая факторов в модель и рассмотреть вариант включая х1 после х2, то результат расчета частного F – критерия для х1 будет иным. Вероятность его случайного формирования составила 0,04%, это значительно меньше принятого стандарта Общий вывод состоит в том, что множественная модель с факторами х1 и х2 с 6. Средние частные коэффициенты эластичности Здесь По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у признака фактора х1, чем признака фактора х2: 0,6% против 0,2%.
Варианты заданий лабораторной работы №3 По 20 предприятиям региона (табл. 11) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).
Таблица 11
где i, j – две последние цифры номера зачетной книжки соответственно
Требуется: 1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

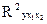 . Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.
. Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации. . Вычисления произведем с помощью следующей таблицы 10;
. Вычисления произведем с помощью следующей таблицы 10;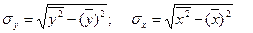
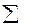








 .
. =0,9699 и r
=0,9699 и r 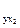 =0,9408). Но в то же время межфакторная связь r
=0,9408). Но в то же время межфакторная связь r  =0,9428 весьма тесная и превышает тесноту связи х2 с у. В связи с этим для улучшения данной модели можно исключить из нее фактор х2 как малоинформативный, недостаточно статистики надежный.
=0,9428 весьма тесная и превышает тесноту связи х2 с у. В связи с этим для улучшения данной модели можно исключить из нее фактор х2 как малоинформативный, недостаточно статистики надежный. =0,7335, связь у и х2 гораздо слабее:
=0,7335, связь у и х2 гораздо слабее:  а межфакторная зависимость х1 и х2 выше, чем парная у и х2:
а межфакторная зависимость х1 и х2 выше, чем парная у и х2:  Все это приводит к выводу о необходимости исключить фактор х2 – доля высококвалифицированных рабочих – из правой части уравнения множественной регрессии.
Все это приводит к выводу о необходимости исключить фактор х2 – доля высококвалифицированных рабочих – из правой части уравнения множественной регрессии. ;
;  .
.
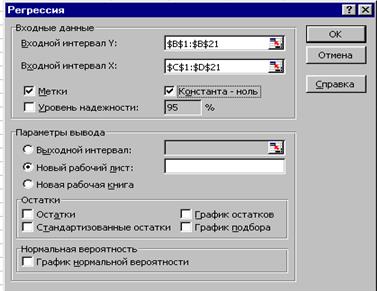





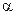 меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%; 5% или 1% вероятности), делают вывод о неслучайной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уравнения. Здесь
меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%; 5% или 1% вероятности), делают вывод о неслучайной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уравнения. Здесь 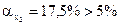 , что позволяет рассматривать х2 как неинформативный фактор и удалить его для улучшения данного уравнения.
, что позволяет рассматривать х2 как неинформативный фактор и удалить его для улучшения данного уравнения. дает F – критерий Фишера:
дает F – критерий Фишера:  .
. .
. оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.
оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом. определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата y в модели факторами х1 и х2.
определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата y в модели факторами х1 и х2.
 .
. показывает статистическую значимость включения фактора х2 в модель после того, как в нее включен фактор х1.
показывает статистическую значимость включения фактора х2 в модель после того, как в нее включен фактор х1. =2. Вероятность случайной природы его значения (Р- значение =0,1750) составляет 17,5% против принятого уровня значимости
=2. Вероятность случайной природы его значения (Р- значение =0,1750) составляет 17,5% против принятого уровня значимости  =0,05 (5%). Следовательно, включение в модель фактора х2 – доля высококвалифицированных рабочих – после того, как в уравнение включен фактор х1 – коэффициент обновления основных фондов – статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака х2 оказывается незначимым, несущественным; фактор х2 включать в уравнение после фактора х1 не следует.
=0,05 (5%). Следовательно, включение в модель фактора х2 – доля высококвалифицированных рабочих – после того, как в уравнение включен фактор х1 – коэффициент обновления основных фондов – статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака х2 оказывается незначимым, несущественным; фактор х2 включать в уравнение после фактора х1 не следует.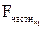 =19,80.
=19,80. содержит неинформативный фактор х2. Если исключить фактор х2, то можно ограничиться уравнением парной регрессии.
содержит неинформативный фактор х2. Если исключить фактор х2, то можно ограничиться уравнением парной регрессии. показывают, на сколько процентов от значения своей средней
показывают, на сколько процентов от значения своей средней  изменяется результат при изменении фактора
изменяется результат при изменении фактора  на 1% от своей средней
на 1% от своей средней  и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости:
и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости: 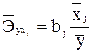 , где bj – коэффициент регрессии при хj в уравнении множественной регрессии.
, где bj – коэффициент регрессии при хj в уравнении множественной регрессии. ,
, 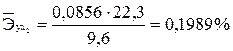 .
.


