
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Альтернативный метод нахождения параметров уравнения парной регрессииСодержание книги
Поиск на нашем сайте Традиционно параметры уравнения парной регрессии
Здесь y – значение зависимой переменной; x – значение независимой переменной;
где yi – значения зависимой переменной, n – объем выборки;
Оценка
где
Выборочный парный коэффициент корреляции показывает тесноту связи между изучаемыми признаками. Он изменяется в пределах [–1; +1]. Если
Sy – выборочное среднеквадратическое отклонение зависимой переменной y. Этот показатель вычисляется по формуле:
где
Sx – выборочное среднеквадратическое отклонение независимой переменной x. Этот показатель вычисляется аналогично среднеквадратическому отклонению зависимого показателя y. При оценивании коэффициента Классический метод наименьших квадратов (МНК) для модели парной регрессии Рассмотрим применение МНК для нахождения оценок неизвестных параметров уравнения регрессии на примере модели линейной парной регрессии. Пусть подобрана эмпирическая линия, по виду которой можно судить о том, что связь между независимой переменной x и зависимой переменной y линейная и описывается функцией:
Необходимо найти такие значения параметров
При минимизации функции (2) значения зависимой Для того чтобы найти минимум функции двух переменных, нужно вычислить частные производные этой функции по каждому из неизвестных параметров и приравнять их к нулю. В результате получаем систему уравнений:
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему:
Это система нормальных уравнений относительно коэффициентов Решением системы нормальных уравнений являются
где
Соv(x,y) – ковариация между зависимым и независимым признаком.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 и
и 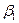 оцениваются с помощью МНК, однако в случае парной регрессионной модели возможен и другой подход к оценке параметров регрессионной функции. Запишем уравнение парной регрессии в следующем виде:
оцениваются с помощью МНК, однако в случае парной регрессионной модели возможен и другой подход к оценке параметров регрессионной функции. Запишем уравнение парной регрессии в следующем виде: .
.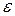 – случайная ошибка;
– случайная ошибка; – среднее значение зависимой переменной, вычисленное на основе выборочных данных. Чаще всего это значение вычисляется по формуле среднего арифметического:
– среднее значение зависимой переменной, вычисленное на основе выборочных данных. Чаще всего это значение вычисляется по формуле среднего арифметического: ,
, ;
; – среднее значение независимой переменной, которое вычисляется аналогично среднему значению зависимой переменной;
– среднее значение независимой переменной, которое вычисляется аналогично среднему значению зависимой переменной;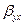 – выборочный коэффициент регрессии y по x. Он характеризует на сколько в среднем изменится результативный показатель y при изменении факторного показателя x на единицу своего измерения.
– выборочный коэффициент регрессии y по x. Он характеризует на сколько в среднем изменится результативный показатель y при изменении факторного показателя x на единицу своего измерения. выборочного коэффициента регрессии y по x вычисляется с помощью следующей формулы:
выборочного коэффициента регрессии y по x вычисляется с помощью следующей формулы: ,
, – выборочный парный коэффициент корреляции, определяемый как
– выборочный парный коэффициент корреляции, определяемый как .
. , то связь между признаками прямая. Если
, то связь между признаками прямая. Если  , то связь между признаками обратная. Если
, то связь между признаками обратная. Если  , то связь между признаками отсутствует. Если
, то связь между признаками отсутствует. Если  или
или  , то связь между изучаемыми признаками является функциональной, т. е. характеризуется полным соответствием между x и y:
, то связь между изучаемыми признаками является функциональной, т. е. характеризуется полным соответствием между x и y:  . Примером функциональной зависимости могут служить математические и статистические формулы, например: S=a2. При таком значении парного коэффициента корреляции регрессионный анализ между изучаемыми показателями не проводится. Данная связь не подлежит численной характеристике, так как на практике массовым социально-экономическим явлениям присущи иные виды связи (в частности, корреляционная связь).
. Примером функциональной зависимости могут служить математические и статистические формулы, например: S=a2. При таком значении парного коэффициента корреляции регрессионный анализ между изучаемыми показателями не проводится. Данная связь не подлежит численной характеристике, так как на практике массовым социально-экономическим явлениям присущи иные виды связи (в частности, корреляционная связь). – среднее арифметическое значение произведения результативного и факторного признаков;
– среднее арифметическое значение произведения результативного и факторного признаков; ,
, – среднее значение квадратов значений результативной переменной y:
– среднее значение квадратов значений результативной переменной y: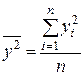 ,
, - квадрат средних значений результативной переменной y:
- квадрат средних значений результативной переменной y: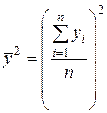 ,
, , но
, но  .
. (1)
(1) и
и  , которые бы доставляли минимум функции:
, которые бы доставляли минимум функции: . (2)
. (2) – уравнение регрессионной модели.(3)
– уравнение регрессионной модели.(3) и независимой
и независимой  переменных известны из
переменных известны из  наблюдений.
наблюдений.

 уравнения регрессии (3):
уравнения регрессии (3): ,
, ,
, – среднее арифметическое значение произведения зависимого и независимого признаков;
– среднее арифметическое значение произведения зависимого и независимого признаков; – дисперсия независимого признака;
– дисперсия независимого признака;


