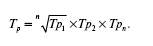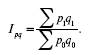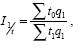Экстраполяция и интерполяция динамических рядов.

Экстраполяция и интерполяция динамических рядов.

Интерполяция и экстраполяция

Для решения неизвестных промежуточных значений динамического ряда применяется способ интерполяции.

Интерполяция – способ определения неизвестных промежуточных значений динамического ряда.

Интерполяция заключается по существу в приближенном отражении сложившейся закономерности внутри определенного отрезка времени – в отличие от экстраполяции, которая требует выхода за пределы этого отрезка времени.

Экстраполяция – метод определения количественных характеристик для совокупностей и явлений, не подвергшихся наблюдению, путем распространения на них результатов, полученных из наблюдения над аналогичными совокупностями за прошедшее время, на будущее и т. д.

Средний уровень ряда динамики характеризует типичную величину абсолютных уровней.

Средний уровень y в интервальных рядах динамики вычисляется с помощью деления суммы уровней y _; на их число n.

В моментном ряду динамики с равностоящими датами времени уровень будет определяться следующим образом:

В моментном ряду динамики с неравностоящими датами средний уровень определяется:

Характеристика обобщающих индивидуальных абсолютных приростов ряда динамики называется средним абсолютным приростом.

Средний абсолютный прирост у определяется так: сумма цепных абсолютных приростов (у_n) делится на их число (n):

Средний абсолютный прирост также может определяться по абсолютным рядам динамики, для этого определяется разность между конечным у_п и базисным у₀ уровнями изучаемого периода, которая делится на m – 1 субпериодов.

Показатель среднего абсолютного прироста определяют по формуле:

Средний темп роста (Т_р) – это индивидуальные темпы роста ряда динамики, которые имеют обобщающую характеристику, ее формула:

Средний темп роста, который определяется по абсолютным уровням динамики, выглядит следующим образом:

На основе взаимосвязи между базисными и цепными темпами роста средний темп роста определяем по формуле:

Средний темп прироста Т_п находится на основании взаимосвязи между темпами роста и прироста. Если существуют сведения о средних темпах роста Т, то для получения средних темпов прироста Тп используется зависимость:

 

Аналитические показатели рядов динамики. Методы изучения рядов динамики.

Основные понятия о рядах динамики

Все процессы и явления, протекающие в общественной жизни человека, являются предметом изучения статистической науки они находятся в постоянном движении и изменении.

Динамическими рядами в статистической науке называют статистические данные, характеризующие изменения явлений во времени, они строятся для выявления и изучения возникающих закономерностей в развитии явлений в различных сферах (например, экономической, политической и культурной) жизни общества.

В рядах динамики имеются два главных элемента:

1) показатель времени (г);

2) уровни развития изучаемого явления (у). В рядах динамики в качестве показателей времени могут выступать определенные даты времени или отдельные периоды.

Уровни, образующие ряды динамики, определяют количественную оценку развития во времени исследуемого явления или процесса, они могут выражаться относительными, абсолютными либо средними величинами. Уровни рядов динамики в зависимости от характера исследуемого явления могут относиться к определенным датам времени или к отдельным периодам.

Динамический ряд состоит из сопоставимых статистических показателей. Для правильности построения динамических рядов необходимо, чтобы состав исследуемой статистической совокупности относился к одной и той же территории, к одному и тому же кругу объектов и был рассчитан по одной и той же методологии.

Данные динамического ряда должны выражаться в одних и тех же единицах измерения, а промежутки времени между значениями ряда должны быть по возможности одинаковыми.

Виды рядов динамики

Ряды динамики подразделяются на моментные, интервальные и ряды средних величин.

Моментные ряды динамики отображают состояние исследуемых процессов на определенные даты времени.

Интервальные ряды динамики отображают итоги развития или функционирования исследуемых процессов за отдельные периоды времени.

Вычисление среднего динамического ряда. Для характеристики процесса за определенный период рассчитывают средний уровень из всех членов динамического ряда.

Способы его расчета зависят от вида динамического ряда. Для интервальных рядов средняя рассчитывается по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных – средняя арифметическая взвешенная.

Для нахождения средних значений моментного ряда применяют среднюю хронологическую:

Средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.

Если интервалы между периодами не равны, то применяется средняя арифметическая взвешенная, а в качестве весов берутся отрезки времени между датами, к которым относятся парные средние смежных значений уровня.

Индивидуальные индексы

Индивидуальные индексы характеризуют соотношение отдельных элементов совокупности.

Примером индивидуальных индексов может быть процент выполнения плана или динамика выпуска одного вида продукции, процент выполнения плана или динамика себестоимости одного вида продукции или соотношение выпуска одного вида продукции за один и тот же период в разных областях.

Индивидуальный индекс обозначается буквой Он определяется методом сопоставления двух величин, характеризующих уровень исследуемого статистического процесса или явления во времени или в пространстве, т. е. за два сравниваемых периода Период (уровень которого сравнивается) называется отчетным. или текущим, периодом и обозначается подстрочным знаком «I» а период, с уровнем которого проводится сравнение, называется базисным и обозначается подстрочным знаком «О» или «ря», если при внутрифирменном планировании сравнение проводится с планом. Если изменение явлений изучается за ряд периодов то каждый период обозначается соответственно подстрочным знаком «О», «1», «2», «3» и т. д.

В статистике количество обозначают буквой «q», цену – «р». себестоимость – «z», затраты времени на производство единицы продукции – «t».

Индивидуальные индексы выражаются следующим образом:

1) индекс физического объема продукции:

где q₁ и q₀ – количество произведенной продукции в отчетном и базисном периодах. Данный индекс характеризует изменение физического объема продукции во времени, в пространстве, если сравнивать производство одного и того же вида продукции за один и тот же период времени, но по разным объектам (заводам, территориям и т. д.), и плана, если фактический выпуск сравнивать с плановым заданием;

2) индекс цен:

где р₁ и р₀ – цена единицы продукции в отчетном и базисном периодах.

Индекс себестоимости:

где z₁ и z₀ – себестоимость единицы продукции в отчетном и базисном периодах. Индекс трудоемкости:

где t₁ и t₀ – затраты времени в отчетном и базисном периодах на производство единицы продукции.

Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:

Приведенные выше индексы: цен, физического объема и товарооборота взаимосвязаны между собой:

Эта взаимосвязь показывает, что изменение товарооборота складывается под воздействием динамики цены и изменения объема продажи данного товара.

Индивидуальные индексы по существу – это относительные величины динамики, выполнения плана или сравнения. Индекс как относительный показатель выражается в виде коэффициентов, когда база для сравнения принимается за единицу, и в процентах, когда база для сравнения принимается за 100.

Базисные и цепные индексы

Для определения статистических индексов нужно иметь данные за два периода или два сравниваемых уровня.

Если существуют данные за определенный ряд периодов или уровней, то в качестве базы для сравнения можно принять один и тот же начальный уровень или уровень предыдущего периода. В первом случае получим индексы с постоянной базой – базисные, а во втором – индексы с переменной базой – цепные.

В экономическом анализе базисные и цепные индексы обладают определенными значениями.

Базисные экономические индексы характеризуют изменение статистических процессов за длительный период времени по отношению к одной отправной точке, но если возникнет необходимость следить за текущими изменениями статистического процесса, то применяются цепные индексы.

Если на основе базисных и цепных индексов исследуется один и тот же период, то это обозначает, что между ними есть взаимосвязь – это произведение цепных индексов, равное базисному Такая взаимосвязь принесет возможность вычислить базисные индексы по данным цепных индексов, и наоборот.

Общие индексы

Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве со–измерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д.

Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода.

Формула общего индекса товарооборота:

Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д.

Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических ин

дексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения.

Расчет агрегатного индекса цен по данной формуле был предложен немецким экономистом Г. Пааше, поэтому его принято называть индексом Пааше.

Другие агрегатные индексы

Рассмотрим некоторые из агрегатных индексов.

1. Индекс себестоимости продукции показывает, во сколько раз себестоимость в отчетном периоде в среднем выше или ниже базисной или плановой себестоимости, а также абсолютный размер экономии или перерасхода в результате изменения себестоимости. Индекс себестоимости – это индекс качественных показате

лей и исчисляется по весам (объему) продукции отчетного периода:

где z₁, – себестоимость единицы продукции в отчетном периоде;

z₀ – себестоимость единицы продукции в базисном (или плановом) периоде;

q₁ – количество продукции в отчетном периоде.

2. Индекс производительности труда. Производительность труда определяется количеством продукции, произведенной в единицу времени, или затратами рабочего времени на производство единицы продукции. Для определения изменения производительности труда в отчетном периоде по сравнению с базисным нужно затраты рабочего времени на производство единицы продукции в базисном периоде (t₀) разделить на затраты рабочего времени на производство единицы продукции в отчетном периоде

3. Индивидуальный индекс производительности труда равен:

Для построения агрегатного индекса производительности труда необходимо затраты рабочего времени на производство одной единицы продукции взвесить на количество продукции, произведенной в отчетном периоде:

где t ₁ q₁ – фактические затраты времени на производство всей продукции в отчетном периоде;

t₀q₁ показывает, сколько времени потребовалось затратить на производство всей продукции отчетного периода в базисном периоде.

Агрегатный индекс производительности труда рассчитывается по объему продукции отчетного периода.

4. Индекс трудоемкости характеризует модификацию трудоемкости единицы продукции в отчетном периоде по сопоставлению с базисным. Величина индекса трудоемкости обратно пропорциональна величине индекса производительности труда, вычисленной по затратам времени на производство единицы продукции. Формула индивидуального индекса:

а агрегатного:

Индекс трудоемкости – это индекс качественных показателей, и рассчитывается он также по весам отчетного периода.

5. Индекс выполнения плана. При его вычислении фактические данные сопоставляются с плановыми, причем весами индекса могут быть показатели плановые и фактические.

6. Среднеарифметический и среднегармонический индексы. Агрегатные индексы цен, физического объема товарооборота

и другие могут быть рассчитаны, если известны индексируемые величины и веса, т. е. p и q. Допустим, что имеется произведение pq и индивидуальные индексы. Возникает проблема построения средних индексов, идентичных агрегатным, путем осреднения индивидуальных индексов. Эта задача решается преобразованием агрегатного индекса в среднеарифметический и среднегармони–ческий индексы. Преобразование агрегатного индекса в среднеарифметический можно рассмотреть на примере агрегатного индекса физического объема товарооборота. В данном случае индивидуальные индексы должны быть взвешены на базисные соизмерители. Из индивидуального индекса физического объема товарооборота i_q = q₁ / q₀ следует, что q₁ = i_q / q₀.

Если заменить q ₁ в числителе агрегатного индекса физического объема товарооборота I_q = Σq₁P₀ / Σq₀P₀ на i_qq₀, то получим i_q = Σi_qq₀p₀ / Σq₀p₀.

Это среднеарифметический индекс физического объема товарооборота.

Но если не известны отдельные значения q₁ и p₁, а дано их произведение q₁p₁ – товарооборот отчетного периода и индивидуальные индексы цен i_p = p₁ / р₀, и сводный индекс рассчитывается с отчетными весами, то применяется среднегармонический индекс цен. Необходимо, чтобы индивидуальные индексы были взвешены так, чтобы среднегармонический индекс совпал с агрегатным. Из формулы i_p = p₁ / р₀ определяем неизвестное значение р₀ и, заменив в формуле агрегатного индекса цен I_p = Σq₁P₁ / Σq₀P₀ значение p₀ = p₁ / i_p, получаем I_p = ΣP₁q₁ / Σ(p₁ / i_p)q₁ = Σp₁q₁ / Σ(p₁q₁ / i_p).

Этот индекс называется среднегармоническим.

7. Индексы средних величин.

Экстраполяция и интерполяция динамических рядов.