
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение уравнения парной регрессии.Содержание книги
Поиск на нашем сайте 1.1. Регрессионный анализ заключается в определении аналитического выражения связи (т.е. в определении вида функции – линейной, степенной и т.д.), в котором изменение одной величины (результативного признака) обусловлено изменением независимой величины (факторного признака). Количественно оценить данную взаимосвязь можно с помощью построения уравнения регрессии или регрессионной функции. Так как получить точное соотношение между изучаемыми экономическими показателями практически невозможно, то в регрессионном анализе в уравнение связи вводится случайная величина Базисной регрессионной моделью является модель парной (однофакторной) линейной регрессии. Данная регрессионная функция называется полиномом первой степени и используется для описания равномерно развивающихся во времени процессов. Общий вид парного линейного уравнения регрессии, описывающего зависимость
где
1) нерепрезентативность выборки. В модель парной регрессии включается один фактор, не способный полностью объяснить вариацию результативного признака, который может быть подвержен влиянию множества других факторов в гораздо большей степени; 2) существует вероятность того, что переменные, участвующие в модели, могут быть измерены с ошибкой. Исходными данными для определения коэффициентов уравнения регрессии
Аналитическая форма зависимости между изучаемой парой признаков (регрессионная функция) определяется с помощью следующих методов: 1)на основе визуальной оценки характера связи. На линейном графике по оси абсцисс откладываются значения факторного (независимого) признака 2)на основе теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности. Параметр Значение параметра 1.2 Нормальная линейная модель парной регрессии Нормальная, или классическая, линейная модель парной регрессии (регрессии с одной переменной) строится исходя из следующих предположений: 1) факторный признак 2) математическое ожидание случайной ошибки уравнения регрессии равно нулю во всех наблюдениях:
3) дисперсия случайной ошибки уравнения регрессии является постоянной для всех наблюдений:
4) случайные ошибки уравнения регрессии не коррелированны между собой, т. е. ковариация случайных ошибок любых двух разных наблюдений равна нулю:
Это предположение верно в том случае, если изучаемые данные не являются временными рядами; 5) основываясь на 3 и 4 предположениях, добавляется условие о том, что случайная ошибка уравнения регрессии является случайной величиной, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией. Исходя из указанных предпосылок, нормальную линейную модель парной регрессии можно записать в следующем виде:
где
Матричная форма нормальной линейной модели парной регрессии:
где
Первый столбец является единичным, так как в уравнении регрессии параметр
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

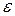 .
. от
от  :
: ,
, – зависимая переменная,
– зависимая переменная,  – независимая переменная;
– независимая переменная; – неизвестные параметры уравнения регрессии, подлежащие оцениванию;
– неизвестные параметры уравнения регрессии, подлежащие оцениванию; и соответствующие им значения независимой переменной
и соответствующие им значения независимой переменной  , измеренные в
, измеренные в  наблюдениях
наблюдениях  (эмпирические данные)
(эмпирические данные) .
. уравнения парной регрессии называется наклоном. Его величина показывает, на сколько в среднем изменится результативный признак
уравнения парной регрессии называется наклоном. Его величина показывает, на сколько в среднем изменится результативный признак  , который называется сдвигом, трактуется как среднее значение результативного признака упри условии, что факторный признак
, который называется сдвигом, трактуется как среднее значение результативного признака упри условии, что факторный признак  ;
; где
где 
 где
где  .
. (1)
(1) (2)
(2) – вектор значений зависимой переменной размерности nх1;
– вектор значений зависимой переменной размерности nх1; – матрица значений независимой переменной размерности nх2.
– матрица значений независимой переменной размерности nх2.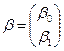 – вектор коэффициентов уравнения регрессии размерности 2х1;
– вектор коэффициентов уравнения регрессии размерности 2х1; – вектор случайных ошибок уравнения регрессии размерности nх1.
– вектор случайных ошибок уравнения регрессии размерности nх1.


