
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение модели множественной регрессии и корреляции: вычисление параметров и оценка статистических характеристикСодержание книги
Поиск на нашем сайте
Цель: оценить возможность применения МНК для определения параметров множественной регрессии и мультиколлинеарность обьясняющих переменных; провести спецификацию модели; оценить параметры и статистическую надежность уравнения множественной регрессии; дать сравнительную оценку силы влияния факторов на результат; оценить целесообразность включения факторов в уравнение множественной регрессии; интерпретировать результаты; использовать при регрессионном моделировании ППП MS Excel.
Теоретические сведения Множественная регрессия – уравнение связи с несколькими независимыми переменными: Для построения уравнения множественной регрессии чаще используют следующие функции: - линейная - - степенная - - экспонента - - гипербола - Для оценки параметров уравнения множественной регрессии применяют МНК. Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
Для ее решения может быть применен метод определителей: Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе: ty= К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (
где Связь коэффициентов множественной регрессии bi со стандартизованными коэффициентами Параметр aопределяется как Коэффициенты «чистой» регрессии bi несравнимы между собой. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии Средние по совокупности коэффициенты эластичности для линейной множественной регрессии рассчитываются по формуле Для расчета частных коэффициентов эластичности применяется следующая формула Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции Для уравнения в стандартизованном масштабе
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов можно определить по формулам: r r Частные коэффициенты корреляции изменяются в пределах от –1 до 1. Качество построенной модели в целом оценивает коэффициент (индекс) детерминации, который рассчитывается как квадрат индекса множественной корреляции: Средняя ошибка аппроксимации и оценка значимости уравнения множественной регрессии в целом определяется аналогично парной регрессии и корреляции. Частный F – критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде фактическое значение частного F критерия для фактора xi определится как Фактическое значение частного F-критерия сравнивается с табличным Fтабл = F ( Оценка значимости коэффициентов чистой регрессии с помощью t – критерия Стьюдента производится аналогично парной регрессии и корреляции, причем справедливо соотношение Постановка задачи По 20 предприятиям региона (табл. 9) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%). Таблица 9
Требуется: 1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , где у – зависимая переменная (результативный признак);
, где у – зависимая переменная (результативный признак);  - независимые переменные (факторы).
- независимые переменные (факторы).
 ;
; ;
; .
.
 ;
;  ; …;
; …;  , где
, где  определитель системы,
определитель системы,  ;…;
;…;  – частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы. , где
, где  стандартизованные переменные;
стандартизованные переменные;  - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии. - коэффициенты) определяются из следующей системы уравнений:
- коэффициенты) определяются из следующей системы уравнений:
 парные коэффициенты корреляции результата с каждым фактором,
парные коэффициенты корреляции результата с каждым фактором,  - коэффициенты межфакторной корреляции.
- коэффициенты межфакторной корреляции. .
. .
. , при этом воздействие остальных факторов считается неизменным.
, при этом воздействие остальных факторов считается неизменным. , где
, где  частное уравнение регрессии, т.е. уравнение регрессии, которое связывает результативный признак y с фактором xi при закреплении факторов x1, x2,…, xi-1, xi+1,…,xp на среднем уровне.
частное уравнение регрессии, т.е. уравнение регрессии, которое связывает результативный признак y с фактором xi при закреплении факторов x1, x2,…, xi-1, xi+1,…,xp на среднем уровне. , причем
, причем  и
и 
 (i=1,…,p).
(i=1,…,p).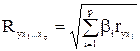 . При линейной зависимости R
. При линейной зависимости R  =
=  , где
, где  определитель матрицы парных коэффициентов корреляции,
определитель матрицы парных коэффициентов корреляции,  определитель матрицы межфакторной корреляции, т.е.
определитель матрицы межфакторной корреляции, т.е.

 или
или =
= 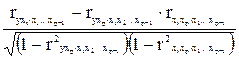 .
.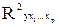 . Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле
. Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле  , где n число наблюдений, m число факторов.
, где n число наблюдений, m число факторов. .
. ;1; n – m – 1). Если
;1; n – m – 1). Если  , то дополнительное включение фактора xi в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi статистически значим. Если
, то дополнительное включение фактора xi в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi статистически значим. Если  , то нецелесообразно включение фактора xi в модель.
, то нецелесообразно включение фактора xi в модель. , а также
, а также  , где
, где  средняя квадратическая ошибка коэффициента регрессии bi.
средняя квадратическая ошибка коэффициента регрессии bi.


