
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение модели нелинейной парной регрессии, анализ статистической значимости и выполнение прогнозаСодержание книги
Поиск на нашем сайте
Цель: провести спецификацию модели; оценить параметры линеаризованного уравнения показательной парной регрессии; проанализировать статистическую значимость показательного уравнения парной регрессии; оценить тесноту связи фактора с результативным признаком; выполнить прогнозирование; интерпретировать результаты; проверить полученные результаты с помощью ППП MS Excel. Теоретические сведения Парная регрессия – уравнение связи двух переменных у и х: где у – зависимая переменная (результативный признак);х – независимая, объясняющая переменная (признак - фактор).Различают линейные и нелинейные регрессии. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Регрессии, нелинейные по объясняющим переменным: - полиномы разных степеней - равносторонняя гипербола Регрессии, нелинейные по оцениваемым параметрам: - степенная - показательная - экспоненциальная При оценке параметров нелинейных регрессий используют МНК, предварительно преобразовывая уравнение к линейному виду: - для равносторонней гиперболы вида - для полулогарифмической кривой Регрессии, нелинейные по оцениваемым параметрам, подразделяются на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью логарифмирования уравнения по основанию e или 10 может быть приведена к линейному виду. Например, для оценки параметров степенной функции Параметр Нелинейная модель внутренне нелинейная (например, Тесноту связи изучаемых явлений оценивает индекс корреляции где Для оценки качества подбора функции рассчитывается квадрат индекса корреляции, называемый индексом детерминации. Индекс детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака: Коэффициент эластичности, средняя ошибка аппроксимации определяются аналогично линейной парной регрессии (см. лабораторную работу №1). Оценка значимости уравнения нелинейной парной регрессии в целом дается с помощью F – критерии Фишера и выполняется аналогично оценке значимости уравнения линейной парной регрессии (см. лабораторную работу №1). Прогнозное значение
Постановка задачи По территориям региона приводятся данные за 199Х год (табл.6). Таблица 6
Продолжение таблицы 6 Требуется: 1. Для характеристики зависимости y от x: а) построить показательное уравнение парной регрессии у от х; б) оценить тесноту связи с помощью индексов корреляции и детерминации; в) оценить качество показательного уравнения парной регрессии с помощью средней ошибки аппроксимации; г) дать оценку силы связи с помощью среднего коэффициента эластичности; д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера. е) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости 2. Проверить полученные результаты с помощью ППП MS Excel. Методические рекомендации и выполнение 1. а) Построению показательной модели y=a·bx предшествует процедура линеаризации переменных. Логарифмируя обе части уравнения, получим: ln y = ln a+ x·lnb. Введем обозначения: Таблица 7
Построим линейное уравнение парной регрессии Y по х. Используя данные таблицы 7, имеем:
Получим линейное уравнение регрессии: Проведя потенцирование уравнения, получим искомую нелинейную показательную модель:
б) Для расчета индекса корреляции Найдем индекс детерминации: Это означает, что 52% вариации заработной платы у объясняется вариацией фактора х – среднедушевого прожиточного минимума. в) Для оценки качества полученной модели найдем среднюю ошибку аппроксимации: В среднем, расчетные значения отклоняются от фактических на 5,851%. Качество построенной модели оценивается как хорошее, т.к. значение г) Для оценки силы связи признаков у и х найдем средний коэффициент эластичности:
Таким образом, в среднем на 0,48% по совокупности изменится среднедневная зарплата от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного на 1%. д) Рассчитаем фактическое значение F – критерия при заданном уровне значимости
Сравнивая табличное Fтабл=4,96 (см. лабораторная работа №1) и фактическое ж) По условию задачи прогнозное значение фактора выше его среднего уровня и прогнозное значение зарплаты при этом составит:
Найдем ошибку прогноза:
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит: Доверительный интервал прогноза при уровне значимости (129,4589; 187,9211). 2. Проверим полученные результаты с помощью ППП MS Excel. Результаты вычисления параметров показательной парной регрессии можно проверить с помощью ППП Excel, для чего используем встроенную статистическую функцию ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН (см. лабораторную работу №1). В результате применения функции ЛГРФПРИБЛ дополнительная регрессионная статистика будет выводиться в порядке, указанном выше (табл. 4 лабораторной работы №1), причем в первой строке таблицы (рис.11) функция ЛГРФПРИБЛ возвращает коэффициенты показательной модели, остальные параметры соответствуют линеаризованной модели (рис.11).
Рис. 11. Результат вычисления функции ЛГРФПРИБЛ
Прогнозное значение результата определим следующим образом: 1) активизируйте Мастер функций, 2) в окне Категория(рис. 12) выберите Статистические, в окне Функция – РОСТ (рис. 3);
Рис.12. Диалоговое окно «Мастер функций»
Рис.13. Диалоговое окно ввода аргументов функции РОСТ 3) заполните аргументы функции (рис.13) Изв знач у – диапазон, содержащий данные результативного признака; Изв знач х – диапазон, содержащий данные факторов независимого признака; Нов _ знач _ х – новые значения х, для которых возвращается соответствующие значения у; Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается свободным образом, если Константа = 0, то свободный член равен 0; В данном случае прогнозируемое значение получилось равным 158,69. Сравнивая полученные вручную и с помощью ППП MS Excel. данные, убеждаемся в правильности выполненных действий.
Варианты заданий лабораторной работы №2 По территориям региона приводятся данные за 199Х год (табл.8). Таблица 8
где i, j две последние цифры номера зачетной книжки соответственно. Требуется: 1. Для характеристики зависимости у от х: а) построить показательное уравнение парной регрессии у от х; б) оценить тесноту связи с помощью индексов корреляции и детерминации; в) оценить качество показательного уравнения парной регрессии с помощью средней ошибки аппроксимации; г) дать оценку силы связи с помощью среднего коэффициента эластичности; д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера. е) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости 2. Проверить полученные результаты с помощью ППП MS Excel.
Вопросы для самопроверки 1. В чем состоят ошибки спецификации модели? 2. Поясните смысл коэффициента регрессии, назовите способы его оценивания. 3. Что такое число степеней свободы и как оно определяется для факторной, остаточной, общей сумм квадратов? 4. Какова концепция F – критерия Фишера для показательной парной регрессии? 5. Каковы методы подбора вида математической функции 6. Какова концепция дисперсионного анализа результатов регрессии? 7. Как находится интервальная оценка прогнозного значения по уравнению регрессии? 8. Запишите все виды моделей, нелинейных относительно: - включаемых переменных; - оцениваемых параметров. 9. В чем отличие применения МНК к моделям, нелинейным относительно включаемых переменных и оцениваемых параметров? 10. Как определяются коэффициенты эластичности? 11. Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков. 12. В чем смысл средней ошибки аппроксимации и как она определяется?
Содержание отчета по лабораторной работе: 1) тема и цель лабораторной работы; 2) текст задания лабораторной работы; 3) результаты, зафиксированные на бумаге, в соответствии с изложенным выше выполнением типового задания лабораторной работы; 4) электронный вариант выполнения лабораторной работы; 5) защита лабораторной работы. Лабораторная работа №3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.009 с.) |

 ,
,




 , заменив
, заменив  на z, получим линейное уравнение регрессии:
на z, получим линейное уравнение регрессии:  и система нормальных уравнений составит:
и система нормальных уравнений составит: 
 , заменив lnx на z, получим линейное уравнение регрессии
, заменив lnx на z, получим линейное уравнение регрессии 
 применяется метод наименьших квадратов к линеаризованному уравнению
применяется метод наименьших квадратов к линеаризованному уравнению 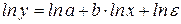 , т.е. решается система нормальных уравнений:
, т.е. решается система нормальных уравнений: 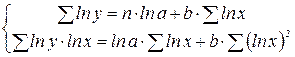 .
. определяется непосредственно из системы, а параметр а – косвенным путем после потенцирования величины lnа.
определяется непосредственно из системы, а параметр а – косвенным путем после потенцирования величины lnа. ) не может быть преобразована в уравнение, линейное по коэффициентам. Для оценки параметров в этом случае используют итеративные процедуры.
) не может быть преобразована в уравнение, линейное по коэффициентам. Для оценки параметров в этом случае используют итеративные процедуры. для нелинейной регрессии
для нелинейной регрессии  :
:  ,
, общая дисперсия результативного признака
общая дисперсия результативного признака 
 - остаточная дисперсия, определяемая исходя из уравнения регрессии
- остаточная дисперсия, определяемая исходя из уравнения регрессии 
 .
. определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения
определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения  . Вычисляется средняя стандартная ошибка прогноза:
. Вычисляется средняя стандартная ошибка прогноза: , где
, где  . и строится доверительный интервал прогноза, границы которого определяются как
. и строится доверительный интервал прогноза, границы которого определяются как 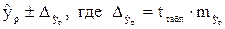 предельная ошибка прогноза.
предельная ошибка прогноза. =0,05.
=0,05. ,
,  ,
,  .Тогда уравнение запишется в виде:
.Тогда уравнение запишется в виде: 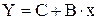 .Параметры полученной линейной модели рассчитываем аналогично тому, как это было сделано в лабораторной работе № 1. Используем данные расчетной таблицы 7
.Параметры полученной линейной модели рассчитываем аналогично тому, как это было сделано в лабораторной работе № 1. Используем данные расчетной таблицы 7
 ,
, .
. .
. .
. .
. .
. .
. – менее 8 %.
– менее 8 %. , где
, где 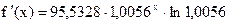 ,
,
 .
. значения, отмечаем, что
значения, отмечаем, что  , это указывает на необходимость отвергнуть гипотезу Н о о статистически незначимых параметрах уравнения показательной парной регрессии.
, это указывает на необходимость отвергнуть гипотезу Н о о статистически незначимых параметрах уравнения показательной парной регрессии. на 5%, тогда оно составляет:
на 5%, тогда оно составляет:  ,
, руб.
руб.
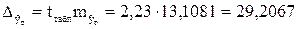 .
.


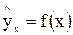 .
.


