
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра: «Математика и информатика»Содержание книги
Поиск на нашем сайте
Кафедра: «Математика и информатика» В.И. Брусова В.А. Гордон Л.И. Шмаркова Методические указания По выполнению лабораторных работ Дисциплина – «Эконометрика» Направление - 521600 «Экономика» Ливны 2002 Авторы: преподаватель кафедры «Математика и информатика» В.И. Брусова__________________ зав. кафедрой «Высшая математика», профессор, д.т.н. В.А. Гордон__________________ доцент кафедры «Высшая математика», к.ф.-м.н. Л.И. Шмаркова__________________
Рецензент: доцент кафедры «Экономика и менеджмент», к.э.н. Е.В.Сибирская __________________
Методические указания и варианты лабораторных работ по курсу «Эконометрика» предназначены для студентов 3-го курса направления 521600 «Экономика» очной формы обучения.
Методические указания рассмотрены и одобрены: на заседании кафедры математики и информатики Ливенского филиала ОрелГТУ «____»_____________________ г., протокол №_______ и рекомендованы к использованию в учебном процессе Зав.кафедрой ___________________Т.Л. Пантелеева
на заседании кафедры высшей математики «____»_____________________ г., протокол №_______ и рекомендованы к использованию в учебном процессе Зав.кафедрой, профессор, д.т.н. ___________________В.А. Гордон
на заседании УМС финансово-экономического факультета «____»_____________________ г., протокол №_______ и допущены к использованию в учебном процессе Председатель УМС, доцент, к.э.н._______________ С.А. Измалкова Содержание стр. Введение 3 1. Требования к знаниям, умениям и навыкам при выполнении лабораторных работ 4 2. Рекомендуемый перечень и содержание лабораторных работ 6 2.1. Лабораторная работа №1 Построение модели линейной парной регрессии, анализ статистической значимости и выполнение прогноза 6 2.2. Лабораторная работа №2 Построение модели нелинейной парной регрессии, анализ статистической значимости и выполнение прогноза 25 2.3.Лабораторная работа №3 Построение модели множественной регрессии и корреляции: вычисление параметров и оценка статистических характеристик 35 2.4.Лабораторная работа №4 Аналитическое выравнивание временногоряда 54 2.5.Лабораторная работа №5 Моделирование временных рядов: оценка адекватности уравнений тренда 68 Литература 98 Приложения 99
Введение В соответствии с учебным планом и рабочей программой по курсу «Эконометрика» каждый студент очной формы обучения (направление 521600 «Экономика») должен выполнить в V семестре 3 курса пять лабораторных работ (№1, №2, №3, №4, №5). Задания лабораторных работ ориентированы на освоение начального курса эконометрики. Изучение этой дисциплины предполагает приобретение студентами опыта построения эконометрических моделей, принятия решения о спецификации и идентификации модели, оценки параметров модели, интерпретации результатов, получения прогнозных оценок. Студенты должны также научиться давать статистическую оценку значимости таких искажающих эффектов, как гетероскедастичность остатков зависимой переменной, мультиколлинеарность объясняющих переменных, автокорреляция. Перед выполнением заданий лабораторных работ рекомендуется ознакомиться /1/, /2/ с соответствующими темам указанного раздела эконометрики: – линейная регрессия и корреляция; – оценка существенности параметров линейной регрессии и корреляции; – интервалы прогноза по линейному уравнению регрессии; – нелинейная регрессия; – корреляция для нелинейной регрессии; – средняя ошибка аппроксимации; – отбор факторов и выбор формы уравнения множественной регрессии; – оценка параметров уравнения множественной регрессии; – частные уравнения регрессии; – множественные и частные корреляции; – оценка надежности результатов множественной регрессии и корреляции; – основные элементы временного ряда; – выявление структуры временного ряда; – автокорреляция уровней временного ряда; – моделирование сезонных и циклических колебаний; – моделирование тенденции временного ряда при наличии структурных изменений; – специфика статистической оценки взаимосвязи временных рядов; – автокорреляция в остатках. Критерий Дарбина-Уотсона; – оценивание параметров уравнений регрессий при наличии автокорреляции в остатках; – динамические эконометрические модели. Все разделы методических указаний имеют идентичную структуру: - краткие методические положения, включающие основные понятия, определения и формулы; - определение целей лабораторной работы; - постановка задачи;
- выполнение типовых заданий лабораторных работ; - указания по реализации типового задания на компьютере с помощью ППП MS Excel; - задания, предлагаемые студентам для самостоятельного выполнения; - вопросы, предлагаемые студентам для контроля; - содержание отчета по лабораторной работе. В конце методических указаний содержатся основные математико-статистические таблицы, необходимые для решения задач.
Требования к знаниям, умениям и навыкам для выполнения Лабораторных работ Значительное ускорение экономических процессов потребовало использование в бизнес-планировании не только арифметических, но и вероятностно-статистических методов, математического моделирования. Сегодня деятельность в любой области экономики (управлении, финансово – кредитной сфере, маркетинге, учете, аудите) требует от специалиста применения современных методов работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство новых методов основано на специальных моделях, концепциях, приемах. Грамотно построенная модель позволяет предвидеть и проконтролировать экономическую ситуацию, основываясь не на интуиции, а на достоверном анализе уже имеющихся данных, а также разработать варианты перспективного развития предприятий. Рабочим инструментом экономического анализирования и прогнозирования является эконометрика. Основной целью изучения эконометрики является овладение эконометрическими методами регрессионного анализа и приложения этих методов к анализу и прогнозированию экономических ситуаций.Главное внимание уделяется построению эконометрических моделей на основе пространственных данных и временных рядов. Выполнение лабораторных работ предусматривает, что студент должен: - знать основные понятия и методы парной, множественной регрессии и корреляции, моделирования тенденции временных рядов, взаимосвязи временных рядов, динамических эконометрических моделей; экономическую интерпретацию формальных математических понятий; - уметь применять эконометрические методы к анализу и прогнозированию экономических ситуаций: построение эконометрических моделей, использование для оценок параметров моделей МНК, двухшаговый МНК, косвенный МНК, построение различных моделей временных рядов, принятие решений о спецификации модели, выбор метода оценки параметров модели; давать статистическую оценку значимости искажающих эффектов: гетероскедастичность остатков зависимой переменной, мультиколлинеарность объясняющих переменных, автокорреляция; выполнять анализ и прогнозирование по данным временным рядам; моделировать тенденцию временных рядов; - владеть эконометрической символикой, основными предпосылками и критериями использования эконометрических методов для оценки взаимосвязей экономических явлений, навыками самостоятельного изучения литературы по эконометрике. Лабораторная работа №1 Построение модели линейной парной регрессии, анализ статистической значимости и выполнение прогноза Цель: провести спецификацию модели; оценить параметры линейной парной регрессии; проанализировать статистическую значимость результатов регрессионного моделирования и качество линейного уравнения парной регрессии; оценить тесноту связи фактора с результативным признаком; выполнить прогнозирование; интерпретировать результаты; проверить полученные результаты с помощью ППП MS Excel.
Теоретические сведения Парная регрессия – уравнение связи двух переменных у и х: где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак - фактор). Различают линейные и нелинейные регрессии. Линейная регрессия: Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. В парной регрессии выбор вида математической функции Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессии, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака Получаем следующую систему нормальных уравнений для оценки параметров а и Параметр Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции
Для оценки качества подбора функции рассчитывается квадрат коэффициента корреляции, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:
Коэффициент эластичности определяется по формуле
Средняя ошибка аппроксимации – среднее отклонение расчетных значений
Оценка значимости уравнения регрессии в целом дается с помощью F – критерии Фишера. При этом выдвигается нулевая гипотеза Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи и выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F – критерия Фишера. Непосредственному расчету F– критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения Любая сумма квадратов отклонений связана с числом степеней свободы, т.е. c числом свободы независимого варьирования признака: n-1=m+(n-m-1), где n – число наблюдений, m – число параметров при переменных х. Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D. Dобщ= Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим F критерий: Fфакт= Табличное значение F – критерия – это максимально возможное значение критерия под влиянием случайных факторов при уровне значимости Если Fфакт> Fтабл , то Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость. Если Fфакт<Fтабл , то гипотеза Н0 не отклоняется и признается статистическая незначимость уравнения регрессии. Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (табл.1) Таблица 1
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t критерии Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t – критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров регрессии и коэффициента корреляции определяются по формулам:
Между F критерием Фишера и t статистикой Стьюдента существует связь, которую можно выразить равенством Критическое (табличное) значение t статистики определяется уровнем значимости Если tфакт> tтабл, то Н0 отклоняется, т.е. a,b,rxy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если tфакт< tтабл, то Н0 не отклоняется и признается случайная природа формирования a,b,rxy Для расчета доверительного интервала определяем предельную ошибку Если в доверительный интервал попадает ноль (т.е. нижняя граница отрицательна, а верхняя положительна), то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения. Прогнозное значение
Постановка задачи По территориям региона приводятся данные за 199Х год (табл.2). Таблица 2
Продолжение таблицы 2 Требуется: 1. Построить поле корреляции. 2. Для характеристики зависимости у от х: а) построить линейное уравнение парной регрессии у от х; б) оценить тесноту связи с помощью коэффициентов корреляции и детерминации; в) оценить качество линейного уравнения с помощью средней ошибки аппроксимации; г) дать оценку силы связи с помощью среднего коэффициента эластичности; д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера. е) оценить статистическую значимость параметров регрессии и корреляции, ж) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости 3. Проверить полученные результаты с помощью ППП МS Excel.
Методические рекомендации и выполнение. 1. Построим поле корреляции, для чего отложим на плоскости в прямоугольной системе координат точки (хi, уi) (рис 1.)
Рис. 1.Поле корреляции 2. Для расчета параметров линейной регрессии строим расчетную таблицу (табл.3.) Таблица 3
а) Построим линейное уравнение парной регрессии у по х. Используя данные таблицы 3, имеем:
Тогда линейное уравнение парной регрессии имеет вид: Оно показывает, что с увеличением среднедушевого прожиточного минимума на 1 руб. средняя зарплата возрастает в среднем на 0,92 руб. б) Учитывая, что
Найдем коэффициент детерминации: Это означает, что почти 52% вариации заработной платы у объясняется вариацией фактора х – среднедушевого прожиточного минимума. в) Для оценки качества полученной модели найдем среднюю ошибку аппроксимации: В среднем, расчетные значения отклоняются от фактических на 5,752%. Качество построенной модели оценивается как хорошее, т.к. значение г) Для оценки силы связи признаков у и х найдем средний коэффициент эластичности: Таким образом, в среднем на 0,5% по совокупности изменится среднедневная зарплата от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного на 1%. д) Для оценки статистической значимости результатов используем F – критерий Фишера. Выдвигаем нулевую гипотезу Но о статистической незначимости полученного линейного уравнения. Рассчитаем фактическое значение F – критерия при заданном уровне значимости
Сравнивая табличное Fтабл=F(0,05;1;10)=4,96 и фактическое е) Оценку статистической значимости параметров регрессии проведем с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигаем гипотезу H0 о статистически незначимом отличии показателей регрессии от нуля: a = b = rxy = 0. Табличное значение t – статистики tтабл при заданном уровне значимости Определим величину случайных ошибок:
Найдем соответствующие фактические значения t – критерия Стьюдента
Фактические значения t – статистики превосходят табличное значение tтабл = 2,23: поэтому гипотеза H0 о статистически незначимом отличии показателей регрессии от нуля отклоняется, т.е. параметры a,b и rxy не случайно отличаются от нуля, а статистически значимы. Для расчета доверительных интервалов для параметров a и b определим их предельные ошибки:
Доверительные интервалы: для параметра a: (23,029; 130,923), для параметра b: (0,297; 1,5436). С вероятностью р = 1 – ж) По условию задачи прогнозное значение фактора выше его среднего уровня и прогнозное значение зарплаты при этом составит:
Найдем ошибку прогноза
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит: Доверительный интервал прогноза: (130,3958; 188,8986). 3. Проверим полученные результаты с помощью ППП MS Excel. Параметры парной регрессии вида y=a + bx определяет встроенная статистическая функция ЛИНЕЙН. Порядок вычисления следующий: 1) ведите исходные данные или откройте существующий файл, содержащий анализируемые данные; 2) выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики; 3) активизируйте Мастер функций любым из способов: а) в главном меню выберете Вставка/Функция; б) на панели Стандартная щелкните по кнопке Вставка функции (в результате появится диалоговое окно Мастер функций (рис. 2)); 4) в окне Категория(рис. 2) выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните по кнопке ОК (в результате появится диалоговое окно ввода аргументов функции ЛИНЕЙН (рис. 3));
Рис.2. Диалоговое окно «Мастер функций»
Рис.3. Диалоговое окно ввода аргументов функции ЛИНЕЙН 5) заполните аргументы функции (рис. 3): Известные значения у – диапазон, содержащий данные результативного признака; Известные значения х – диапазон, содержащий данные факторов независимого признака; Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается свободным образом, если Константа = 0, то свободный член равен 0; Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения Щелкните кнопкой ОК; 6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме (табл. 4) Таблица 4
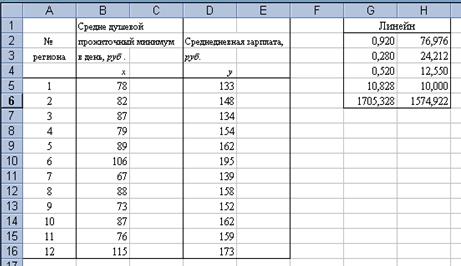
Для данных рассматриваемого примера результат вычисления функции ЛИНЕЙН представлен на рис. 4
Рис.4. Результат вычисления функции ЛИНЕЙН
Замечание. С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий: 1) проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис / Настройки. Установите флажок Пакет анализа (рис. 5);
Рис.5. Подключение надстройки Пакет анализа
2) в главном меню выберите Сервис / Анализ данных / Регрессия (рис. 6). Щелкните по кнопке ОК;
Рис.6. Диалоговое окно Анализ данных 3) заполните диалоговое окно ввода данных и параметров вывода (рис. 7): Входной интервал Y – диапазон, содержащий данные результативного признака; Входной интервал Х – диапазон, содержащий данные факторов независимого признака; Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет; Константа – нуль – флажок, указывающий на наличие или на отсутствие свободного члена в уравнении; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Новый рабочий лист – можно задать произвольное имя нового листа. Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните кнопкой ОК. Результаты регрессионного анализа для данных рассматриваемой задачи представлены на рис. 8
Рис.7. Диалоговое окно ввода параметров инструмента Регрессия
Рис.8. Результаты применения инструмента Регрессия Прогнозное значение результата определим следующим образом: 1) активизируйте Мастер функций, 2) в окне Категориявыберите Статистические, в окне Функция – ТЕНДЕНЦИЯ (рис. 9);
Рис.9. Диалоговое окно «Мастер функций»
Рис.10. Диалоговое окно ввода аргументов функции ТЕНДЕНЦИЯ 3) заполните аргументы функции (рис.10.): Изв знач у – диапазон, содержащий данные результативного признака; Изв знач х – диапазон, содержащий данные факторов независимого признака; Нов _ знач _ х – новые значения х, для которых возвращается соответствующие значения у; Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается свободным образом, если Константа = 0, то свободный член равен 0; В данном случае прогнозируемое значение получилось равным 159,686. Сравнивая полученные вручную и с помощью ППП MS Excel. данные, убеждаемся в правильности выполненных действий. Варианты заданий лабораторной работы №1 По территориям региона приводятся данные за 199Х год (табл.5). Таблица 5
где i, j две последние цифры номера зачетной книжки соответственно. Требуется: 1. Построить поле корреляции. 2. Для характеристики зависимости у от х: а) построить линейное уравнение парной регрессии у от х; б) оценить тесноту связи с помощью коэффициентов корреляции и детерминации; в) оценить качество линейного уравнения с помощью средней ошибки аппроксимации; г) дать оценку силы связи с помощью среднего коэффициента эластичности; д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера. е) оценить статистическую значимость параметров регрессии и корреляции, ж) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 7% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости 3. Проверить полученные результаты с помощью ППП MS Excel. Вопросы для самопроверки 1. В чем состоят ошибки спецификации модели? 2. Поясните смысл коэффициента регрессии, назовите способы его оценивания. 3. Что такое число степеней свободы и как оно определяется для факторной, остаточной, общей сумм квадратов? 4. Какова концепция F – критерия Фишера для линейной парной регрессии? 5. Как оценивается значимость параметров уравнения регрессии? 6. Каковы методы подбора вида математической функции 7. Какова концепция дисперсионного анализа результатов регрессии? 8. Как находится интервальная оценка прогнозного значения по уравнению регрессии? 9. Как определяются коэффициенты эластичности? 10. В чем смысл средней ошибки аппроксимации и как она определяется?
Содержание отчета по лабораторной работе: 1) тема и цель лабораторной работы; 2) текст задания лабораторной работы; 3) результаты, зафиксированные на бумаге, в соответствии с изложенным выше выполнением типового задания лабораторной работы; 4) электронный вариант выполнения лабораторной работы; 5) защита лабораторной работы. Лабораторная работа №2 Теоретические сведения Парная регрессия – уравнение связи двух переменных у и х: где у – зависимая переменная (результативный признак);х – независимая, объясняющая переменная (признак - фактор).Различают линейные и нелинейные регрессии. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Регрессии, нелинейные по объясняющим переменным: - полиномы разных степеней - равносторонняя гипербола Регрессии, нелинейные по оцениваемым параметрам: - степенная - показательная - экспоненциальная При оценке параметров нелинейных регрессий используют МНК, предварительно преобразовывая уравнение к линейному виду: - для равносторонней гиперболы вида | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 ,
,
 может быть осуществлен тремя методами: графическим; аналитическим; экспериментальным. Аналитический метод основан на изучении материальной природы связи исследуемых признаков. Экспериментальный метод основан на сравнении величины остаточной дисперсии, рассчитанный при разных моделях. Графический метод достаточно нагляден и основан на поле корреляции.
может быть осуществлен тремя методами: графическим; аналитическим; экспериментальным. Аналитический метод основан на изучении материальной природы связи исследуемых признаков. Экспериментальный метод основан на сравнении величины остаточной дисперсии, рассчитанный при разных моделях. Графический метод достаточно нагляден и основан на поле корреляции. от теоретических
от теоретических  минимальна, т.е.
минимальна, т.е. 
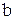 :
:  решая которую либо методом последовательного исключения переменных, либо методом определителей, находят искомые оценки параметров а и
решая которую либо методом последовательного исключения переменных, либо методом определителей, находят искомые оценки параметров а и  ;
;  , где
, где 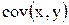 - ковариация признаков,
- ковариация признаков,  - дисперсия признака х,
- дисперсия признака х, 

 для линейной регрессии
для линейной регрессии 
 , причем
, причем 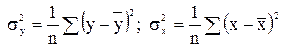
 .
. первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Средний коэффициент эластичности
первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Средний коэффициент эластичности  показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения.
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения.
 - относительная ошибка аппроксимации. Возможно и иное определение средней ошибки аппроксимации:
- относительная ошибка аппроксимации. Возможно и иное определение средней ошибки аппроксимации:  Ошибка аппроксимации в пределах 5 – 7% свидетельствует о хорошем подборе модели к исходным данным. Допустимый предел значений
Ошибка аппроксимации в пределах 5 – 7% свидетельствует о хорошем подборе модели к исходным данным. Допустимый предел значений 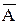 - не более 8 – 10%.
- не более 8 – 10%.
 на две части – “объясненную” (или “факторную”, т.е.
на две части – “объясненную” (или “факторную”, т.е.  ) и “необъясненную” (или остаточную, т.е.
) и “необъясненную” (или остаточную, т.е.  ):
): 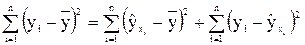 .
. ; Dфакт=
; Dфакт=  ; Dост=
; Dост= 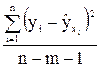 .
.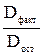 или Fфакт=
или Fфакт= 
 и данных степенях свободы (k1=m; k2=n-m-1). Уровень значимости
и данных степенях свободы (k1=m; k2=n-m-1). Уровень значимости 
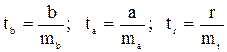


 - остаточная дисперсия на одну степень свободы:
- остаточная дисперсия на одну степень свободы:  .
. .
. для каждого показателя:
для каждого показателя: 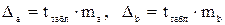 и границы доверительных интервалов имеют вид:
и границы доверительных интервалов имеют вид:  .
. определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения
определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения  . Вычисляется средняя стандартная ошибка прогноза:
. Вычисляется средняя стандартная ошибка прогноза: и строится доверительный интервал прогноза, границы которого определяются как
и строится доверительный интервал прогноза, границы которого определяются как 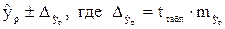 предельная ошибка прогноза.
предельная ошибка прогноза.

 ,
, .
. .
. ,
,  оценим тесноту линейной связи с помощью линейного коэффициента парной корреляции:
оценим тесноту линейной связи с помощью линейного коэффициента парной корреляции: .
. .
. .
. – менее 8 %.
– менее 8 %. .
.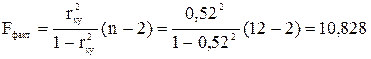 .
. значения, отмечаем, что
значения, отмечаем, что  , что указывает на необходимость отвергнуть выдвинутую гипотезу Но.
, что указывает на необходимость отвергнуть выдвинутую гипотезу Но. ,
,  ,
,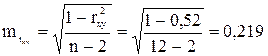 .
. ,
,  ,
, .
. ,
,  ,
, 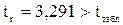 ,
, ,
, .
. на 5%, тогда оно составляет:
на 5%, тогда оно составляет: 
 159,6472 руб.
159,6472 руб. .
. .
.







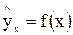 ?
?




 , заменив
, заменив 


