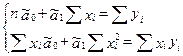Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная модель множественной регрессии.Содержание книги
Поиск на нашем сайте
Система сост из равенств:1)y=a0+a1*x1+a2*x2+u; 2)E(u/x1,xt)=0; 3)E(u2/x1,x2)=r2u.x1,x2-экзоген перем, y-эндоген перемен.случ возмещен предполаг гомоскедастичн.спецификация содержит 4 параметра.это модель линейная эконометрич в виде изолир уравнений с несколькими объясняющ перемен или модель лин множ регрессии.эконом смысл коэф-ов а1 и а2-ожидаемые предельн знач перемен у по перемен х.это базовая модель,т.к.1)к такой модели мб приближенна практич любая эконометрич модель в виде изолир уравнения;2)поведен ур-ия в линейн моделях имеют такой же вид. эконометрич инвестиц модель Самуэльсона-Хикса явл частн случаем модели Метод наименьших квадратов: алгоритм метода; условия применения. В матем статистике методы получения наилучшего приближ к исходным данным в виде аппроксимирующей функции назыв регрессионным анализом. Его основн задачами явл установление завис-сти между переменными и оценка(прогноз)значений завис переменной.В экон исслед-ях часто заданному значению одной переменной может соответств множество значений другой переменной,т.е. каждому значению одной переменной соответствует условное распределение другой переменной.Зав-сть, при к-рой каждому знач одной перемен соответств условное матем ожидание другой назыв регрессионной. 1) построим модель в виде линейного уравнений парной регрессии:yt=a0+a1xt+ut.Постановка задачи. Дано: выборка наблюдений за поведением переменных ytи xt.Найти:1.Оценки значений параметров а.2.Оценки точности.3.Оценку рассеяния случ возмущения.4.Оценку точности прогнозирования
1. Выборка
3. В е к т о р а
4. Матрица коэффициентов при параметрах
Идея метода. При оценивании пар-ров регр.моделей наиболее часто применяется МНК. Его оценки обладают такими стат.св-вами: несмещенность, состоятельность, эффективность. Достоинство МНК: простота мат.выводов и вычислит-х процедур. Пусть имеем выборку из 4-х точек (n=4): P1 =(x1, y1),P2 =(x2, y2), P3 =(x3, y3), P4 =(x4, y4) На практике мы имеем возможность наблюдать только исходные точки Предполагаем, что существует теоретическая прямая, которая наилучшим образом проходит через них
Задача: оценить с некоторой точностью, как может проходить эта прямая
.Условиями минимума функции являются равенство нулю первых производных и положительность вторых производных по ã0 и ã1. Задача оценки параметров парной регр.модели МНК сводится к задаче определения экстремума (минимума) ф-ии 2х аргументов
Система называется системой нормальных уравнений для вычисления оценок параметров уравнения парной регрессии. Упростим систему нормальных уравнений.
Убеждаемся, что решение системы уравнений будет соответствовать минимуму функции. Для этого вычисляем значения вторых частных производных функции
Для решения системы выразим из первого уравнения ã0, подставим его во второе уравнение. Получим:
Проанализируем выражение. Для этого вычислим COV(x,y) и σ2(x).Получим: Проверим выполнение условия несмещенности для оценки. Для этого вычислим числитель выражения.Получаем: Вычислим дисперсии параметров уравнения регрессии и дисперсию прогнозирования эндогенной переменной. С помощью МНК получили 1)Оценки параметров уравнения регрессии, по крайней мере, состоятельными 2)Если случайное возмущение подчиняется нормальному закону распределения, то оценки параметров модели несмещенные и эффективные 3)Нет необходимости в знании закона распределения случайных возмущений. преимущества МНК: - не требуется знания закона распределения случайного возмущения - дает оценки по крайней мере состоятельные - в случае нормального распределения случайного возмущения оценки параметров линейной модели несмещенные и эффективные 2. Для получения несмещенных и эффективных оценок параметров в случае, если случайное возмущение имеет закон распределения отличный от нормального, необходимо наложить на него дополнительные требования
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.83 (0.01 с.) |

 Введем следующие обозначения и определения
Введем следующие обозначения и определения 2. Система уравнений наблюдений
2. Система уравнений наблюдений



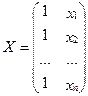
 Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия:
Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия: