Статистические характеристики выборки и генеральной совокупности статистических данных. Их соотношения.

Генеральная совокупность – это всё множество объектов, обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени, входящих в предмет изучения в соответствии с программой исследования. В социальных науках под объектами исследования и, соответственно, выборку составляют люди, но генеральную совокупность также могут составлять другие объекты (домохозяйства, предприятия, населенные пункты и т.д.).

Выборка – это некоторая часть объектов генеральной совокупности, которая выступает в качестве объектов непосредственного изучения.

Выборка (Выборочная совокупность) – часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.

В основе статистических выводов проведенного исследования лежит распределение случайной величины X, наблюдаемые же значения(х₁, х₂, …,х_n)называются реализациями случайной величины Х (n — объем выборки). Распределение случайной величины X в генеральной совокупности носит теоретический, идеальный характер, а выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е.их параметры определяют значение функции распределения F(x) в каждой точке пространства возможных значений случайной величины X. Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное.Важнейшими параметрами распределений являются математическоеожидание E(x) и дисперсия .

По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное.Выборочными аналогами параметров E(x) и для него являются: среднее значение и эмпирическая дисперсия . Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания E(x) этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком X (она обозначена буквой p); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p).Дисперсия же альтернативного распределения также имеет эмпирический аналог .

В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения..

Долей выборки k_n называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

k_n = n/N.

Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n:

w = n_n/n.

Пример. В партии товара, содержащей 1000 ед., при 5% выборке долявыборки k_n в абсолютной величине составляет 50 ед. (n = N*0,05); если же в этой выборке обнаружено 2 бракованных изделия, то выборочная доля брака w составит 0,04 (w = 2/50 = 0,04 или 4%).

Так как выборочная совокупность отлична от генеральной, то возникают ошибки выборки.

Связь: E(Xв(с чертой))=Хо(с чертой)

Е(Дв)=((n -1)/³)*До

Д(Хв(с чертой))=До/n

Схема Гаусса – Маркова.

В рамках модели (1)

величины выборки (2) связаны следующей системой линейных алгебраических уравнений:

……………………..

Она называется системой уравнений наблюдений объекта в рамках линейной модели (1), или, иначе, схемой Гаусса – Маркова. Компактная запись:

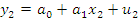
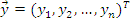где – вектор наблюденных значений эндогенной переменной y модели (1);

- ненаблюдаемый вектор случайных возмущений (остатков);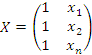

– матрица наблюденных значений предопределенной переменной x модели (1), расширенная (при наличии в функции регрессии определяемого коэффициента ) столбцом единиц;

Наконец, - вектор неизвестных коэффициентов функции регрессии модели, подлежащий оцениванию по выборке (2).

Теорема Гаусса-Маркова

Пусть матрица X уравнений наблюдений имеет размер , где , и обладает линейно-независимыми столбцами, а случайные возмущения удовлетворяют четырем условиям:

Тогда:

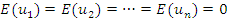
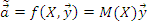А) Наилучшая линейная процедура имеет вид:

Б) Эффективная линейная несмещенная оценка обладает свойством наименьших квадратов:

В) Ковариационная матрица оценки вычисляется по правилу

Г) Несмещенная оценка параметра модели находится по формуле

где n – число уравнений наблюдений, k+1 – количество неизвестных коэффициентов функции регрессии модели.