Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автокорреляция случайного возмущения. Причины. Последствия.Содержание книги
Поиск на нашем сайте
Автокорреляция случайного возмущения. Причины. Последствия. Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость. Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное. Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов Причина – неправильный выбор спецификации модели. Последствия автокорреляции - оценки коэффициентов теряют эффективность; - стандартные ошибки коэффициентов занижены
Авторегрессия 1-го порядка: AR(1)
Авторкорреляция скользящих средних 3-го порядка: Алгоритм проверки адекватности парной регрессионной модели. Адекватность – возможность получения результата с удовлетворительной точностью. Применительно к построению эконометрических моделей под точностью результата понимается абсолютное значение разности между прогнозом, полученным с помощью модели и реальным значением эндогенной переменной. Тогда модель считается адекватной, если эта разность не превосходит некоторого наперед заданного. 1.Вся имеющаяся в распоряжении выборка наблюдений делится на две неравные части: обучающую и контролирующую Обучающая выборка включает основную (большую) часть наблюдений Контролирующая выборка содержит до 5% от общего объема выборки 2.По обучающей выборке оценивается модель (рассчитываются оценки параметров модели и их стандартные ошибки). 3.Задается значение доверительной вероятности Рдов =1-α и определяется критическое значение дроби Стьюдента tкрит 4.Для каждой «точки» из контролирующей выборки по известным значениям экзогенных переменных строится доверительный интервал прогнозного значения эндогенной переменной (12.5). 5.Проверяется попадает ли соответствующее значение эндогенной переменной внутрь полученного Пункты 5 и 6 проводятся для каждой точки выборки персонально! Вывод. Если все значения эндогенных переменных из контрольной выборки накрываются соответствующими доверительными интервалами, то полученная модель с вероятностью Рдов считается адекватной, т.е. пригодной для дальнейшего использования в целях решения экономических задач Алгоритм проверки значимости регрессора в парной регрессионной модели. При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b. Алгоритм проверки значимости параметра b выполняется в следующей последовательности: 1) оценка параметров парной регрессии 2) оценка дисперсии возмущений 3) оценка 4) выбор значения tкр (по заданному уровню значимости альфа и числу степеней свободы (n-2) из таблиц распределения Стьюдента) 5) проверка неравенства Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость. Идея метода. При оценивании пар-ров регр.моделей наиболее часто применяется МНК. Его оценки обладают такими стат.св-вами: несмещенность, состоятельность, эффективность. Достоинство МНК: простота мат.выводов и вычислит-х процедур. Пусть имеем выборку из 4-х точек (n=4): P1 =(x1, y1),P2 =(x2, y2), P3 =(x3, y3), P4 =(x4, y4) На практике мы имеем возможность наблюдать только исходные точки Предполагаем, что существует теоретическая прямая, которая наилучшим образом проходит через них Задача: оценить с некоторой точностью, как может проходить эта прямая
.Условиями минимума функции являются равенство нулю первых производных и положительность вторых производных по ã0 и ã1. Задача оценки параметров парной регр.модели МНК сводится к задаче определения экстремума (минимума) ф-ии 2х аргументов
Система называется системой нормальных уравнений для вычисления оценок параметров уравнения парной регрессии. Упростим систему нормальных уравнений.
Убеждаемся, что решение системы уравнений будет соответствовать минимуму функции. Для этого вычисляем значения вторых частных производных функции
Для решения системы выразим из первого уравнения ã0, подставим его во второе уравнение. Получим:
Проанализируем выражение. Для этого вычислим COV(x,y) и σ2(x).Получим: Проверим выполнение условия несмещенности для оценки. Для этого вычислим числитель выражения.Получаем: Вычислим дисперсии параметров уравнения регрессии и дисперсию прогнозирования эндогенной переменной. С помощью МНК получили 1)Оценки параметров уравнения регрессии, по крайней мере, состоятельными 2)Если случайное возмущение подчиняется нормальному закону распределения, то оценки параметров модели несмещенные и эффективные 3)Нет необходимости в знании закона распределения случайных возмущений. преимущества МНК: - не требуется знания закона распределения случайного возмущения - дает оценки по крайней мере состоятельные - в случае нормального распределения случайного возмущения оценки параметров линейной модели несмещенные и эффективные 2. Для получения несмещенных и эффективных оценок параметров в случае, если случайное возмущение имеет закон распределения отличный от нормального, необходимо наложить на него дополнительные требования Модели временных рядов. Большую роль в эконометрике играет анализ и моделирование на базе данных по одному объекту, но на основе множества последовательных моментов или периодов времени, т. е. на основе временных рядов (рядов динамики). Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов. Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (Е) компонент. Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение -мультипликативные модели временного ряда. Аддитивная модель имеет вид: Y = Т + S + Е; мультипликативная модель: Y=T* S • Е, где Т- тренд, S- сезонная составляющая, Е – случайная составляющая Модели временных рядов. К этому классу относятся модели: • тренда: y(t) = T(t) +ξt где t – время; T(t) - временной тренд заданного параметрического вида (например, линейный T(t) = a + bt); ξ t - случайная (стохастическая) компонента; • сезонности: y(t) = S(t) + ξt где S(t) - периодическая (сезонная) компонента, ξt - случайная (стохастическая) компонента. • тренда и сезонности: y(t) = T(t) + S(t) + ξt (аддитивная) или y(t) = T(t)S{t) + ξt (мультипликативная)
Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.). Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д. СМОТРИ ВОПРОС 29 СМОТРИ ВОПРОС 35. СМОТРИ ВОПРОС 35 Свойства временных рядов Временной ряд – это датированная целочисленными моментами времени t экономическая переменная 1 класс: факторы («вековые» воздействия), результирующее влияние которых на данный объект на протяжении длительного отрезка времени не изменяют своего направления. Они порождают монотонную составляющую (тенденцию или тренд). 2 класс: факторы (циклические воздействия), результирующее влияние которых на объект совершает законченный круг в течение некоторого фиксированного промежутка времени T. 3 класс: факторы (случайные воздействия), результирующее влияние которых на объект с высокой скоростью меняет направление и интенсивность. 3 Класс факторов позволяют интерпретировать величину СМОТРИ ВОПРОС 56 58.Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений. Один из принципов спецификации - включение в спецификацию экономической модели случайных возмущений. На практике не всегда удается учесть влияние всех факторов на изучаемую переменную (например, в функции спроса учесть возрастные особенности потребителя), выбрать правильную форму математической зависимости между экономическими переменными (например, нелинейную вместо линейной), безошибочно выполнить измерения (правильно провести опрос). Поэтому эндогенные переменные модели следует рассматривать как случайные величины и, помимо детерминированной составляющей, описывающей поведение эндогенной переменной в зависимости от предопределенных переменных, включать некоторые случайные величины, называемые случайные возмущения. Y = f(x)+Ɛ, где f(x)- часть эндогенной переменной, объясняемая значением экзогенной переменной Х; ε – случайное возмущение. Для того чтобы среди множества уравнений регрессии выбрать одно, необходим критерий отбора. При оценивании параметров регрессионных моделей наиболее часто применяется МНК. Его оценки обладают свойствами несмещённости, состоятельности, эффективности:
То есть оценки параметров должны быть подобраны таким образом, чтобы сумма квадратов случайных возмущений стремилась к минимуму
Для нахождения минимума дифференцируем (1):
Получаем стандартную форму нормальных уравнений:
Из которых находим параметры. Схема Гаусса – Маркова. В рамках модели (1)
величины выборки (2)
……………………..
Она называется системой уравнений наблюдений объекта в рамках линейной модели (1), или, иначе, схемой Гаусса – Маркова. Компактная запись:
где
Наконец, Теорема Гаусса-Маркова Пусть матрица X уравнений наблюдений
Тогда: А) Наилучшая линейная процедура
Б) Эффективная линейная несмещенная оценка
В) Ковариационная матрица оценки Г) Несмещенная оценка параметра где n – число уравнений наблюдений, k+1 – количество неизвестных коэффициентов функции регрессии модели. Тест Стьюдента Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента
где S остаточная дисперсия на одну степень свободы Данный критерий затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2). Этот же результат можно получить после извлечения корня из F-критерия, т.е. tb= Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует о том, что в парной линейной регрессии t2r=F. Кроме того t2b=F, следовательно, t2r= t2b. Таким образом проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии. Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт - принимаем или отвергаем гипотезу H0. Если tтабл < tфакт, то H0 отклоняется, т.е. a и b не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования a и b. 66. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей. Типы переменных: эндогенные – образуются внутри модели. Экзогенные – не зависят от модели, внешние для модели. Модель, возникающая на этапе спецификации, как правило, имеет структурную форму, отражающую заложенные в модель экономические утверждения. В такой форме эндогенные переменные модели, как правило, не выражены явно через ее экзогенные переменные. При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведенной форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели. Приведенная форма модели непосредственно предназначена для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных. В частном случае структурная форма модели может совпадать с приведенной формой. Переход от структурной к приведенной форме возможен всегда и однозначно, а обратное неверно. Приведенная форма.
Структурная форма. 67. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей. СМОТРИ ВОПРОС 66 Автокорреляция случайного возмущения. Причины. Последствия. Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость. Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное. Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов Причина – неправильный выбор спецификации модели. Последствия автокорреляции - оценки коэффициентов теряют эффективность; - стандартные ошибки коэффициентов занижены
Авторегрессия 1-го порядка: AR(1)
Авторкорреляция скользящих средних 3-го порядка:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.95.233 (0.012 с.) |

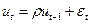
 Типы автокорреляции. Модели с автокоррелированными остатками называются авторегрессионными. Рассматриваем модель парной регрессии,
Типы автокорреляции. Модели с автокоррелированными остатками называются авторегрессионными. Рассматриваем модель парной регрессии,
 Авторегрессия 5-го порядка: AR(5)
Авторегрессия 5-го порядка: AR(5)
 среднего квадратичного отклонения параметра b
среднего квадратичного отклонения параметра b при Н0: b=0
при Н0: b=0 Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия:
Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия:
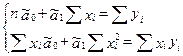





 где T(t) - временной тренд заданного параметрического вида; S(t) - периодическая (сезонная) компонента; ξt - случайная (стохастическая) компонента.
где T(t) - временной тренд заданного параметрического вида; S(t) - периодическая (сезонная) компонента; ξt - случайная (стохастическая) компонента. . Эта переменная служит количественной характеристикой некоторого экономического объекта, поэтому изменение этой переменной во времени определяется факторами, оказывающими воздействие на данный объект с ходом времени. Все факторы делятся на 3 класса.
. Эта переменная служит количественной характеристикой некоторого экономического объекта, поэтому изменение этой переменной во времени определяется факторами, оказывающими воздействие на данный объект с ходом времени. Все факторы делятся на 3 класса. зависит от переменной времени t, т.е.
зависит от переменной времени t, т.е.  . Следовательно, от переменной времени t зависят и основные количественные характеристики временного ряда
. Следовательно, от переменной времени t зависят и основные количественные характеристики временного ряда  .
. (1)
(1) (2)
(2)





 связаны следующей системой линейных алгебраических уравнений:
связаны следующей системой линейных алгебраических уравнений:

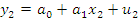


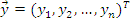 – вектор наблюденных значений эндогенной переменной y модели (1);
– вектор наблюденных значений эндогенной переменной y модели (1); - ненаблюдаемый вектор случайных возмущений (остатков);
- ненаблюдаемый вектор случайных возмущений (остатков);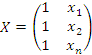 – матрица наблюденных значений предопределенной переменной x модели (1), расширенная (при наличии в функции регрессии определяемого коэффициента
– матрица наблюденных значений предопределенной переменной x модели (1), расширенная (при наличии в функции регрессии определяемого коэффициента  ) столбцом единиц;
) столбцом единиц; - вектор неизвестных коэффициентов функции регрессии модели, подлежащий оцениванию по выборке (2).
- вектор неизвестных коэффициентов функции регрессии модели, подлежащий оцениванию по выборке (2). , где
, где  , и обладает линейно-независимыми столбцами, а случайные возмущения
, и обладает линейно-независимыми столбцами, а случайные возмущения 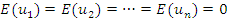



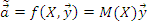 имеет вид:
имеет вид:


 модели находится по формуле
модели находится по формуле 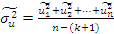
 где mb – стандартная ошибка параметра
где mb – стандартная ошибка параметра  ,
, . Аналогично для параметра а.
. Аналогично для параметра а.