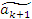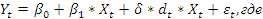Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отражение в эконометрических моделях фактора времени.Содержание книги
Поиск на нашем сайте
Определение. Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими. Определение. Переменные, связанные с моментом времени, называются датированными. Необходимость соотнесения переменных модели к моменту времени является третьим принципом спецификации модели. Переменные, которые относятся к предыдущим моментам времени, называются Лаговыми. Значения датированных переменных в различные дискретные моменты времени (например, значения x0, x1, x2,… располагаемого душевого дохода потребителя в рамках модели конкурентного рынка при t=0,1,2…) называются временными рядами. Таким образом, временным рядом называют такую экономическую модель, в которой эндогенная переменная Yt является функцией целочисленного аргумента t. Оценивание линейной модели множественной регрессии в Excel.
Алгоритм использования процедуры «ЛИНЕЙН» в приложении EXCEL: 1.Подготовка таблицы исходных данных (Записываем в столбцы значения переменных).
2.Вызов процедуры «ЛИНЕЙН» (Выделяем диапазон ячеек 5×(k+1), нажимаем на значок функции, в диалоговом окне «Категория» выбираем, «Статистические» в диалоговом окне «Выберите функцию» - «Линейн»; щелкнуть мышью по кнопке ОК). 3.Ввод исходных данных в процедуру (В строчке «Известные_значения_y» диалогового окна указать адрес диапазона значений эндогенной переменной yt, а в строчке «Известные_значения_х» - адрес диапазона известных значений предопределенных переменных x11:xkn; в строчку «Конст» диалогового окна занести цифру 1, если есть свободный член и 0, если его нет. В строчку «Статистика» диалогового окна занести цифру 1, Нажать клавиши Ctrl + Shift + Enter).
4. Анализ результата
Оценивание линейной модели множественной регрессии методом наименьших квадратов (МНК) в Excel с использованием сервиса ЛИНЕЙН СМОТРИ ВОПРОС 35. Оценивание регрессионной модели с фиктивной переменной наклона; значение параметра при фиктивной переменной. Определение. Фиктивной переменной модели называют переменную, которая вводится для учета качественных факторов и принимающая дискретные числовые значения Фиктивные переменные участвуют в моделях одновременно с другими типами переменных. Они так же могут быть отнесены к определенному моменту времени. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона. Фиктивная переменная наклона изменяет наклон линии регрессии. При помощи фиктивных переменных наклона можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или налоговых ограничений, изменение политической ситуации и т. д.). Для учета возможного изменения наклона графика модели при изменении градации качественного фактора предлагается ввести в спецификацию модели еще одно слагаемое вида «d умноженное на x». Спецификация регрессионной модели в этом случае (например, для парной регрессионной модели, для простоты) имеет вид:
dt = 0 – до структурных изменений 1 – после структурных изменений, dt - бинарная переменная Фиктивная переменная входит в уравнение в мультипликативной форме. Оценки параметров рассчитываются с помощью метода наименьших квадратов. Параметр при фиктивной переменной характеризует степень изменения наклона графика функции регрессии под воздействием качественного фактора.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.204 (0.009 с.) |

 Из теории известно, что все переменные объекта изменяются со временем. Этот факт должен быть отражен в моделях. Для этого каждой переменной, которая изменяется со временем добавляется индекс “t”. Например, Ydt означает, что переменная - «уровень спроса» - относится к текущему моменту времени. На примере модели конкурентного рынка имеем:
Из теории известно, что все переменные объекта изменяются со временем. Этот факт должен быть отражен в моделях. Для этого каждой переменной, которая изменяется со временем добавляется индекс “t”. Например, Ydt означает, что переменная - «уровень спроса» - относится к текущему моменту времени. На примере модели конкурентного рынка имеем: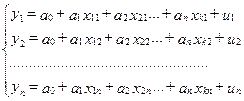 Модель множественной регрессии имеет вид:
Модель множественной регрессии имеет вид: