
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы сглаживания временного ряда.Содержание книги
Поиск на нашем сайте Методы «механического» сглаживания Метод усреднения по двум половинам ряда, когда ряд делится на две части. Затем, рассчитываются два значения средних уровней ряда, по которым графически определяется тенденция ряда. Очевидно, что такой тренд не достаточно полно отражает основную закономерность развития явления. Метод укрупнения интервалов, при котором производится увеличение протяженности временных промежутков, и рассчитываются новые значения уровней ряда. Метод скользящей средней. Данный метод применяется для характеристики тенденции развития исследуемой статистической совокупности и основан на расчете средних уровней ряда за определенный период. Метод экспоненциальной средней. Экспоненциальная средняя – это адаптивная скользящая средняя, рассчитанная с применением весов, зависящих от степени «удаленности» отдельных уровней ряда от среднего значения. Величина веса убывает по мере удаления уровня по хронологической прямой от среднего значения в соответствии с экспоненциальной функцией, поэтому такая средняя называется экспоненциальной. На практике применяется многократное экспоненциальное сглаживания ряда динамики, которое используется для прогнозирования развития явления. Способы, включенные в первую группу, ввиду применяемых методик расчета предоставляют исследователю очень упрощенное, неточное, представление о тенденции в ряду динамики. Однако корректное применение этих способов требует от исследователя глубины знаний о динамике различных социально - экономических явлений. Методы «аналитического» выравнивания Более точным способом отображения тенденции динамического ряда является аналитическое выравнивание, т. е. выравнивание с помощью аналитических формул. В этом случае динамический ряд выражается в виде функции у (t), в которой в качестве основного фактора принимается время t, и изменения аргумента функции определяют расчетные значения уt. Чаще всего при выравнивании используются следующий зависимости: параболическая экспоненциальная Модели временных рядов. Большую роль в эконометрике играет анализ и моделирование на базе данных по одному объекту, но на основе множества последовательных моментов или периодов времени, т. е. на основе временных рядов (рядов динамики). Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов. Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (Е) компонент. Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение -мультипликативные модели временного ряда. Аддитивная модель имеет вид: Y = Т + S + Е; мультипликативная модель: Y=T* S • Е, где Т- тренд, S- сезонная составляющая, Е – случайная составляющая Модели временных рядов. К этому классу относятся модели: • тренда: y(t) = T(t) +ξt где t – время; T(t) - временной тренд заданного параметрического вида (например, линейный T(t) = a + bt); ξ t - случайная (стохастическая) компонента; • сезонности: y(t) = S(t) + ξt где S(t) - периодическая (сезонная) компонента, ξt - случайная (стохастическая) компонента. • тренда и сезонности: y(t) = T(t) + S(t) + ξt (аддитивная) или y(t) = T(t)S{t) + ξt (мультипликативная)
Кроме того, существуют модели временных рядов, в которых присутствует циклическая компонента, формирующая изменения анализируемого признака, обусловленные действием долговременных циклов экономической демографической или астрофизической природы (волны Кондратьева, циклы солнечной активности и т.д.). Модели временных рядов могут применяться для изучения и прогнозирования объема продаж туристических путевок, спроса на железнодорожные и авиабилеты, при краткосрочном прогнозировании процентных ставок и т.д.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.007 с.) |

 ;
; ;
;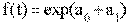 или
или  ).
). где T(t) - временной тренд заданного параметрического вида; S(t) - периодическая (сезонная) компонента; ξt - случайная (стохастическая) компонента.
где T(t) - временной тренд заданного параметрического вида; S(t) - периодическая (сезонная) компонента; ξt - случайная (стохастическая) компонента.


