
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест ошибочной спецификации Рамсея.Содержание книги
Поиск на нашем сайте
Тест Рамсея позволяет проверить, стоит ли начинать поиск дополнительной переменной для включения в уравнение 1. Оценивается уравнение регрессии 2. Вычисляются степени оценок зависимой переменной 3. Оценивается уравнение регрессии с этими степенями 4. Проводится оценка улучшения по F-критерию Тест Стьюдента Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Для оценки значимости коэффициента регрессии его величину сравнивают с его стандартной ошибкой, т.е. определяют фактическое значение t-критерия Стьюдента
где S остаточная дисперсия на одну степень свободы Данный критерий затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2). Этот же результат можно получить после извлечения корня из F-критерия, т.е. tb= Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует о том, что в парной линейной регрессии t2r=F. Кроме того t2b=F, следовательно, t2r= t2b. Таким образом проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о значимости линейного уравнения регрессии. Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт - принимаем или отвергаем гипотезу H0. Если tтабл < tфакт, то H0 отклоняется, т.е. a и b не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования a и b. 66. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей. Типы переменных: эндогенные – образуются внутри модели. Экзогенные – не зависят от модели, внешние для модели. Модель, возникающая на этапе спецификации, как правило, имеет структурную форму, отражающую заложенные в модель экономические утверждения. В такой форме эндогенные переменные модели, как правило, не выражены явно через ее экзогенные переменные. При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведенной форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели. Приведенная форма модели непосредственно предназначена для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных. В частном случае структурная форма модели может совпадать с приведенной формой.
Переход от структурной к приведенной форме возможен всегда и однозначно, а обратное неверно. Приведенная форма.
Структурная форма. 67. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей. СМОТРИ ВОПРОС 66 Устранение автокорреляции в парной регрессии Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов. Причина – неправильный выбор спецификации модели. Последствия автокорреляции ( оценки коэффициентов теряют эффективность, стандартные ошибки коэффициентов занижены). Для устранения автокорреляции можно воспользоваться процедурой Кохрейна-Орката: 1)По выборочным данным выполняется настройка модели и вычисляется вектор остатков регрессии е. 2)По остаткам регрессии оценивается модель авторегрессии: 3)С оценкой 4)Строится новый вектор остатков, и процедура повторяется (начиная с П.2). Итерационный процесс заканчивается при условии совпадения оценок на последней и предпоследней итерациях с заданной степенью точности.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.164.22 (0.009 с.) |

 где mb – стандартная ошибка параметра
где mb – стандартная ошибка параметра  ,
, . Аналогично для параметра а.
. Аналогично для параметра а.



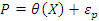

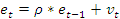
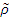 выполняются преобразования (1) и (2).
выполняются преобразования (1) и (2).


