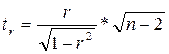Прогнозирование экономических переменных. Проверка адекватности модели

Экономическое прогнозирование (ЭП) - это процесс разработки экономических прогнозов, основанных на научных методах познания экономических явлений и использования всей совокупности методов, средств и способов экономической прогностики.

Рассмотрим две переменные x и y, где y - зависимая переменная (регрессант, эндогенная переменная), x – независимая переменная (регрессор, экзогенная переменная). Переменная у характеризует результат или эффективность функционирования анализируемой экономической системы и ее значения формируются внутри системы под воздействием ряда других переменных или факторов. По своей природе объясняемая переменная всегда стохастична (случайна). Переменная х – это переменная, которая по своей природе может быть как случайной так и неслучайной. Эта переменная поддается управлению и планирования, ее называют объясняющей переменной. Если объясняющую переменную можно задавать «извне» анализируемой системы, то ее называют экзогенной.

Функция y = f(Х^*) называется функцией регрессии у по Х, если она описывает изменение условного среднего значения результирующей переменной у в зависимости от изменения переменных Х. Соотношение между переменными будем обозначать: y = f (x).

f(X) = E(y| X = X^*) = E(y| X^*)

или сокращенно

f(X) = E(y| X).

В регрессионной анализе результирующая переменная у может быть рассмотрена как функция, значения которой можно определить, используя значения объясняющих переменных Х = (х⁽¹⁾, х⁽²⁾,…, х^(k)). Математически это можно записать в виде уравнения регрессионной зависимости

у(Х)=f(Х)+ε(X),

E(ε(X))= 0.

Здесь ε(Х) – случайная составляющая. Она отражает влияние на фактор у, не учтенных в модели объясняющих переменных Х, а также включает в себя возможные случайные погрешности измерения объясняемой переменной у. Второе тождество в системе следует непосредственно из смысла линейной регрессии. Поскольку

f(X)= E(y(X)|X)=E(f(X))+E(ε(X))

и E(f(X))= f(X) (так как величина f(X) при фиксированном значении Х не является случайно), то E(ε(X))= 0 при любом фиксированном значении Х.

Сложность экономических процессов и явлений затрудняют проверку их адекватности, истинности получаемых результатов.

Модель именуется адекватной, если прогнозы значений эндогенной переменной согласуются с её наблюденными значениями.

В целом для проверки адекватности модели используются различные тесты, например- Коэффициент детерминации, F-тест, Тест Стьюдента, Ошибка аппроксимации, Тест Дарбина- Уотсона и тест Голфелда-Квандта.

Тест Голфелда-Квандта предназначен для проверки предпосылки теоремы Гаусса-Маркова о гомоскедастичности случайных возмущений в уравнениях наблюдений, т.е. о том, что Var(u₁)=Var(u₂)=….=Var(u_n)=σ²

Тест Дарбина-Уотсона. Этот тест предназначен для проверки третьей Cov(u_i;u_j)=0 при i≠j. Часто истинной причиной неадекватности предпосылки оказывается ошибка в выборе уравнения регрессии в спецификации модели. Данный тест является одним из наиболее важных тестов в эконометрике.

Ошибка аппроксимации. Величина отклонений фактических и расчетных значений результативного признака (y-ˆy_x) по каждому признаку представляет собой ошибку аппроксимации (ОА). Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ОА как среднюю арифметическую простую.

или , где n-число наблюдений

F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера. F_факт определяется как

F= (R2/k)/((1-R2)/n-k-1)= ESS/k)/(RSS/n-k-1), где n — число единиц совокупности;

m - число параметров при переменных х

F_табл – это максимально возможное значение критерия под влия­нием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть пра­вильную гипотезу при условии, что она верна. Обычно а принимает­ся равной 0,05 или 0,01.

Если F_табл<F_факт, то Н₀ - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл>F_факт, то гипотеза Н₀ не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R²

0≤ R²≤1. причем если R²= 1 то переменная полностью объясняется регрессором x_t.

Тест Стьюдента. Отношение коэффициента регрессии к его стандартной ошибке дает t-статистику, которая подчиняется статистике Стьюдента при (n-2) степенях свободы. Эта статистика применяется для проверки статистической значимости коэффициента регрессии и для расчета его доверительного интервала.

Фактическое значение t-критерия Стьюдента определяется как