
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 47 – Множественная регрессия и корреляцияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Начало можно взять в билете №45 В тех случаях, когда необходимо оценить влияние нескольких факторов на исследуемую величину, строится уравнение множественной регрессии. Если связь является линейной, то уравнение линейной множественной регрессии запишется в виде: где m - число учитываемых факторов (независимых переменных), n - объем выборки. Рассмотрим случай, когда y зависит от двух переменных – x1 и x2. Уравнение с оцененными параметрами будет иметь вид: Чтобы определить значения коэффициентов a0, a1 и a2, воспользуемся методом наименьших квадратов. Как и ранее, задача формулируется следующим образом: Приравняв частные производные нулю и выполнив преобразования, получим систему уравнений: Решив систему, можно получить формулы для расчета коэффициентов уравнения множественной линейной регрессии (a0, a1, a2). Рассмотрим более общий случай - зависимость переменной y от m факторов. Обозначим: A = {aj}, j = 0, 1, 2,..., m - вектор оценок параметров регрессии; Y = {yi}, X = {xij}, при этом m - количество независимых переменных, n - объем выборки. Уравнение регрессии может быть представлено в следующим образом. Для конкретного yi: i = a0 + a1xi1 + a2xi2 +... + amxim, или в матричном виде: Y = A ∙ X,
Обратите внимание на то, что в матрицу X дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что в уравнении (6.5) свободный член a0 умножается на фиктивную переменную xi0, принимающую значение 1 для всех i. Можно показать, что для общего случая множественной линейной регрессии, коэффициенты уравнения могут быть определены из следующего соотношения: A = (Xт∙X)-1∙Xт∙Y. (6.6) Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и её направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин. Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственный характер. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «бо́льшее количество пожарных приводит к бо́льшему ущербу», и тем более не имеет смысла попытка минимизировать ущерб от пожаров путем ликвидации пожарных бригад.В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Параметрические показатели корреляции Ковариация Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка. Ковариация определяется как математическое ожидание произведения отклонений случайных величин:
где E - математическое ожидание. Свойства ковариации: · Ковариация двух независимых случайных величин и равна нулю. · Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий. · Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа. Линейный коэффициент корреляции Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле:
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости:
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния». Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или Непараметрические показатели корреляции: Коэффициент ранговой корреляции Кендалла Коэффициент ранговой корреляции Спирмена Коэффициент корреляции знаков Фехнера Коэффициент множественной ранговой корреляции (конкордации) Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации) Ограничения корреляционного анализа: · Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно быть не менее, чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию не менее, чем в 10 раз превышающую количество факторов). В случае, если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний. · Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае, если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения. · Исходная совокупность значений должна быть качественно однородной. · Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора. Область применения Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи. Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.235.195 (0.007 с.) |

 = a0 + a1xi1 + a2xi2 +... + amxim,
= a0 + a1xi1 + a2xi2 +... + amxim, 
 = a0 + a1xi1 + a2xi2,
= a0 + a1xi1 + a2xi2,  .
.

 , либо коэффициент корреляции R. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
, либо коэффициент корреляции R. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.


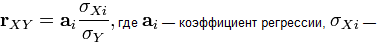 среднеквадратическое отклонение соответствующего факторного признака.
среднеквадратическое отклонение соответствующего факторного признака. (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
(тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).


