
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Предмет «анализ данных на компьютере»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос. Предмет «Анализ данных на компьютере» В нашей повседневной жизни, бизнесе, иной профессиональной деятельности, а также в научных исследованиях мы постоянно сталкиваемся с событиями и явлениями с неопределенным исходом. При этом нам постоянно приходится принимать в подобных неопределенных, связанных со многими случайностями ситуациях свои решения, иногда очень важные. В быту или в несложном бизнесе мы можем принимать такие решения на основе здравого смысла, интуиции, предыдущего опыта. Здесь мы часто можем сделать некий «запас прочности» на действие случая: скажем, выходить из дома на десять минут раньше, чтобы уже почти наверняка не опаздывать на работу. Однако в более серьезном бизнесе, в условиях жесткой конкуренции, решения должны приниматься на основе тщательного анализа имеющейся информации, быть обоснованными и доказуемыми.(Например, банк) Для решения задач, связанных с анализом данных при наличии случайных и непредсказуемых воздействий, математиками и другими исследователями за последние двести лет был выработан мощный и гибкий арсенал методов, называемых в совокупности математической статистикой (а также прикладной статистикой или анализом данных). Эти методы позволяют выявлять закономерности на фоне случайностей, делать обоснованные выводы и прогнозы, давать оценки вероятностей их выполнения или невыполнения. Вопрос. Основные задачи анализа данных на компьютере Анализ данных позволяют выявлять закономерности на фоне случайностей, делать обоснованные выводы и прогнозы, давать оценки вероятностей их выполнения или невыполнения. Вопрос. Случайные переменные и законы их распределения Каждая случайная величина задает распределение вероятностей на множестве своих значений. Если ξ — случайная величина, принимающая значения из X, то мы можем задать распределение вероятностей Pξ на X следующим образом: Pξ(A) = P(ξ ∈ A). Виды случайных величин. В практических задачах обычно используются два вида случайных величин — дискретные и непрерывные, хотя бывают и такие случайные величины, которые не являются ни дискретными, ни непрерывными. Дискретные случайные величины обладают тем свойством, что мы можем перечислить (перенумеровать) все их возможные значения. Таким образом, для задания распределения вероятностей, порожденных дискретными случайными величинами, надо только указать вероятности каждого возможного значения этой случайной величины. Определение. Случайную величину называют дискретной, если множество ее возможных значений конечно, либо счетно. Каждое возможное значение дискретной случайной величины имеет положительную вероятность (иногда, впрочем, допускают, что некоторые значения могут иметь нулевые вероятности, особенно когда рассматривают не одно, а несколько дискретных распределений одновременно). Функция распределения. Пусть ξ обозначает случайную величину, принимающую вещественные значения, x — вещественное число. Определение. Функцией распределения F(x) случайной величины ξ называют F(x) = P(ξ<= x). Ясно, что функция F(x) монотонно возрастает с ростом x. Непрерывные случайные величины. Определение. Случайную величину, принимающую вещественные значения, называют непрерывной, если непрерывна ее функция распределения. Непрерывным в этом случае называют и соответствующее распределение вероятностей. Плотность вероятности.(НСВ) Определение. Функция p(t) называется плотностью вероятности в точке t (иногда — плотностью случайной величины ξ ), если для любых чисел a, b (пусть a < b ) P(a < ξ < b) = Вопрос. Распределения дискретной случайной переменной. Полигон распределения. Вопрос. Распределения непрерывной случайной переменной. Функция распределения. Вопрос. Плотность распределения. Построение графика на компьютере Определение. Случайная величина ξ имеет нормальное распределение вероятностей с параметрами a и σ2, если ее плотность распределения задается формулой: в excel: НОРМРАСП (Х; среднее; стандартное_откл; интегральная) Х — аргумент функции; Среднее (µ) — среднее арифметическое распределения; Стандартное_откл ( σ) — стандартное отклонение распределения; Интегральная — логическое значение, определяющее форму функции. Вопрос. Типичные величины дискретной случайной переменной (?) Дискретные случайные величины обладают тем свойством, что мы можем перечислить (перенумеровать) все их возможные значения. Таким образом, для задания распределения вероятностей, порожденных дискретными случайными величинами, надо только указать вероятности каждого возможного значения этой случайной величины. Определение. Случайную величину называют дискретной, если множество ее возможных значений конечно, либо счетно. Каждое возможное значение дискретной случайной величины имеет положительную вероятность (иногда, впрочем, допускают, что некоторые значения могут иметь нулевые вероятности, особенно когда рассматривают не одно, а несколько дискретных распределений одновременно). Свойства дисперсии Приведем здесь основные свойства дисперсии. Свойство 1. Дисперсия постоянной величины С равна нулю:
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
Свойство 3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:
Перечисленные свойства дисперсии используются при вычислениях, когда мы имеем дело с несколькими случайными величинами. Из свойств 1 и 3 следует важный вывод: D(X + C) = D(X), где С — постоянная величина. Кроме того, справедлива следующая теорема. ТЕОРЕМА. Дисперсия числа появления события А в п независимых испытаниях с вероятностью появления р в каждом из них этого события вычисляется по формуле
Биномиальное распределение Биномиальное распределение — дискретное распределение вероятностей случайной величины
Распределение Пуассона Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона — это частный случай биномиального распределения. Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
Нормальное распределение Нормальное распределение, также называемое гауссовым распределением, гауссианой или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
· отклонение при стрельбе · некоторые погрешности измерений (однако, многие погрешности приборов в технике имеют сильно не нормальные распределения) · рост живых организмов Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Плотность вероятности Функция распределения
Распределение Стьюдента Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Распределение Парето. Распределе́ние Паре́то в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений, являющихся степенными. Называется по имени Вилфредо Парето.
Плотность вероятности Функция распределения
Доказательство Линейный коэффициент корреляции связан с коэффициентом регрессии в виде следующей зависимости: Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния». Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или Непараметрические показатели корреляции. Коэффициент ранговой корреляции Кендалла Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
где
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
Коэффициент ранговой корреляции Спирмена Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности
Коэффициент корреляции знаков Фехнера Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают. H — число пар, у которых знаки отклонений значений от их средних не совпадают. Коэффициент множественной ранговой корреляции (конкордации)
Значимость:
В случае наличия связанных рангов:
Свойства коэффициента корреляции Неравенство Коши — Буняковского: если принять в качестве скалярного произведения двух случайных величин ковариацию
Коэффициент корреляции равен
где
Доказательство Если Корреляционный анализ Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используякоэффициент детерминации). Ограничения корреляционного анализа
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю. Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно быть не менее, чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию не менее, чем в 10 раз превышающую количество факторов). В случае, если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний. Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае, если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.. Исходная совокупность значений должна быть качественно однородной. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора. Область применения Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи. Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Простая корреляция R или
Для коэффициента регрессии может быть рассчитана его ошибка репрезентативности. Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на отношение квадратических отношений:
Критерий достоверности коэффициента регрессии вычисляется по обычной формуле:
в итоге он равен критерию достоверности коэффициента корреляции:
Достоверность величины tR устанавливается по таблице Стьюдента при = n - 2, где n - число пар наблюдений.
Криволинейная регрессия. РЕГРЕССИЯ, КРИВОЛИНЕЙНАЯ. Любая нелинейная регрессия, в которой уравнение регрессии для изменений в одной переменной (у) как функции t изменений в другой (х) является квадратичным, кубическим или уравнение более высокого порядка. Хотя математически всегда возможно получить уравнение регрессии, которое будет соответствовать каждой "загогулине" кривой, большинство этих пертурбаций возникает в результате ошибок в составлении выборки или измерении, и такое "совершенное" соответствие ничего не дает. Не всегда легко определить, соответствует ли криволинейная регрессия набору данных, хотя существуют статистические тесты для определения того, значительно ли увеличивает каждая более высокая степень уравнения степ совпадения этого набора данных. Аппроксимация кривой выполняется тем же путем с использованием метода наименьших квадратов, что и выравнивание по прямой линии. Линия регрессии должна удовлетворять условию минимума суммы квадратов расстояний до каждой точки корреляционного поля. В данном случае в уравнении (1) у представляет собой расчетное значение функции, определенное при помощи уравнения выбранной криволинейной связи по фактическим значениям х j. Например, если для аппроксимации связи выбрана парабола второго порядка, то y = а + b x + cx2, (14).а разность между точкой, лежащей на кривой, и данной точкой корреляционного поля при соответствующем аргументе можно записать аналогично уравнению (3) в виде yj = yj (a + bx + cx2) (15) При этом сумма квадратов расстояний от каждой точки корреляционного поля до новой линии регрессии в случае параболы второго порядка будет иметь вид: S 2 = yj 2 = [yj (a + bx + cx2)] 2 (16) Исходя из условия минимума этой суммы, частные производные S 2 по а, b и с приравниваются к нулю. Выполнив необходимые преобразования, получим систему трех уравнений с тремя неизвестными для определения a, b и с., y = m a + b x + c x 2 yx = a x + b x 2 + c x 2. yx2 = a x 2 + b x 3 + c x4. (17). Решая систему уравнений относительно a, b и с, находим численные значения коэффициентов регрессии. Величины y, x, x2, yx, yx2, x3, x4.находятся непосредственно по данным производственных измерений. Оценкой тесноты связи при криволинейной зависимости служит теоретическое корреляционное отношение xу, представляющее собой корень квадратный из соотношения двух дисперсий: среднего квадрата р2 отклонений расчетных значений y' j функции по найденному уравнению регрессии от среднеарифметического значения Y величины y к среднему квадрату отклонений y2 фактических значений функции y j от ее среднеарифметического значения: xу = { р2 / y2 } 1/2 = { (y' j - Y)2 / (y j - Y)2 } 1/2 (18) Квадрат корреляционного отношения xу2 показывает долю полной изменчивости зависимой переменной у, обусловленную изменчивостью аргумента х. Этот показатель называется коэффициентом детерминации. В отлично от коэффициента корреляции величина корреляционного отношения может принимать только положительные значения от 0 до 1. При полном отсутствии связи корреляционное отношение равно нулю, при наличии функциональной связи оно равно единице, а при наличии регрессионной связи различной тесноты корреляционное отношение принимает значения между нулем и единицей. Выбор типа кривой имеет большое значение в регрессионном анализе, поскольку от вида выбранной взаимосвязи зависит точность аппроксимации и статистические оценки тесноты связи. Наиболее простой метод выбора типа кривой состоит в построении корреляционных полей и в подборе соответствующих типов регрессионных уравнений по расположению точек на этих полях. Методы регрессионного анализа позволяют отыскивать численные значения коэффициентов регрессии для сложных видов взаимосвязи параметров, описываемых, например, полиномами высоких степеней. Часто вид кривой может быть определен на основе физической сущности рассматриваемого процесса или явления. Полиномы высоких степеней имеет смысл применять для описания быстро меняющихся процессов в том случае, если пределы колебания параметров этих процессов значительные. Применительно к исследованиям металлургического процесса достаточно использовать кривые низших порядков, например параболу второго порядка. Эта кривая может иметь один экстремум, что, как показала практика, вполне достаточно для описания различных характеристик металлургического процесса. Результаты расчетов параметров парной корреляционной взаимосвязи были бы достоверны н представляли бы практическую ценность в том случае, если бы используемая информация была получена для условий широких пределов колебаний аргумента при постоянстве всех прочих параметров процесса. Следовательно, методы исследования парной корреляционной взаимосвязи параметров могут быть использованы для решения практических задач лишь тогда, когда существует уверенность в отсутствии других серьезных влияний на функцию, кроме анализируемого аргумента. В производственных условиях вести процесс таким образом продолжительное время невозможно. Однако если иметь информацию об основных параметрах процесса, влияющих на его результаты, то математическим путем можно исключить влияние этих параметров и выделить в “чистом виде” взаимосвязь интересующей нас функции и аргумента. Такая связь называется частной, или индивидуальной. Для ее определения используется метод множественной регрессии. Корреляционное отношение. Корреляционное отношение и индекс корреляции - это числовые характеристики, тесно связанные понятием случайной величины, а точнее с системой случайных величин. Поэтому для введения и определения их значения и роли необходимо пояснить понятие системы случайных величин и некоторые свойства присущие им. Два или более случайные величины, описывающих некоторое явление называют системой или комплексом случайных величин. Систему нескольких случайных величин X, Y, Z, …, W принято обозначать через (X, Y, Z, …, W). Например, точка на плоскости описывается не одной координатой, а двумя, а в пространстве - даже тремя. Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных случайных величин, входящих в систему, а включают также взаимные связи (зависимости) между случайными величинами. Поэтому при изучении системы случайных величин следует обращать внимание на характер и степень зависимости. Эта зависимость может быть более или менее ярко выраженной, более или менее тесной. А в других случаях случайные величины оказаться практически независимыми. Случайная величина Y называется независимой от случайной величины Х, если закон распределения случайной величины Y не зависит от того какое значение приняла величина Х. Следует отметить, что зависимость и независимость случайных величин есть всегда явление взаимное: если Y не зависит от Х, то и величина Х не зависит от Y. Учитывая это, можно привести следующее определение независимости случайных величин. Случайные величины Х и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины Х и Y называются зависимыми. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Понятие "зависимости" случайных величин, которым пользуются в теории вероятностей, несколько отличается от обычного понятия "зависимости" величин, которым пользуются в математике. Так, математик под "зависимостью" подразумевает только один тип зависимости - полную, жесткую, так называемую функциональную зависимость. Две величины Х и Y называются функционально зависимыми, если, зная значение одного из них, можно точно определить значение другой. В теории вероятностей встречаются несколько с иным типом зависимости - вероятностной зависимостью. Если величина Y связана с величиной Х вероятностной зависимостью, то, зная значение Х, нельзя точно указать значение Y, а можно указать её закон распределения, зависящий от того, какое значение приняла величина Х. Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Т.о., функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай - полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости - от самой сильной до самой слабой. Вероятностная зависимость между случайными величинами часто встречается на практике. Если случайные величины Х и Y находятся в вероятностной зависимости, то это не означает, что с изменением величины Х величина Y изменяется вполне определенным образом; это лишь означает, что с изменением величины Х величина Y имеет тенденцию также изменяться (возрастать или убывать при возрастании Х). Эта тенденция соблюдается лишь в общих чертах, а в каждом отдельном случае возможны отступления от неё.
Смысл случайных ошибок ОШИБОК ТЕОРИЯ - раздел математич. статистики, посвященный построению уточненных выводов о численных значениях приближенно измеренных, величин, а также об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, т. <к. каждое измерение содержит нек-рую ошибку. Различают три основных вида ошибок: систематические, грубые и случайные. Систематические ошибки все время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определенных причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематич. ошибок производится с помощью методов, выходящих за пределы математич. статистики (см. Наблюдений обработка). Грубые ошибки возникают в результате просчета, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов. О. т. занимается изучением лишь грубых и случайных ошибок. Основные задачи О. т.: разыскание законов распределения случайных ошибок, разыскание оценок (см. Оценка статистическая).неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и установление грубых ошибок. Пусть в результате пнезависимых равноточных измерений нек-рой неизвестной величины m, получены значения Y1, Y2,..., Yn. Разности
наз. истинными ошибками. В терминах вероятностной О. т. все di трактуются как случайные величины; независимость измерений понимается как взаимная независимость случайных величин d1,..., dn. Равноточность измерений в широком смысле истолковывается как одинаковая распределенность: истинные ошибки равноточных измерений суть одинаково распределенные случайные величины. При этом математич. ожидание истинных ошибок
а разности
наз. кажущимися ошибками. Выбор
Опыт показывает, что практически очень часто случайные ошибки di подчиняются распределениям, близким к нормальному (причины этого вскрыты т. н. предельными теоремами теории вероятностей). В этом случае величина Если дисперсия s2 отдельных измерений заранее неизвестна, то для ее оценки пользуются величиной
(
подчиняется Стъюдента распределению с п-1 степенями свободы. Этим можно воспользоваться для оценки погрешности приближенного равенства Величина (п-1)s2/s2 при тех же предположениях имеет "хи-квадрагп" распределение с n-1 степенями свободы. Это позволяет оценить погрешность приближенного равенства
где F(z, п-1) - функция c2 –распределения
Если нек-рые измерения содержат грубые ошибки, то предыдущие правила оценки m и s дадут искаженные результаты. Поэтому очень важно уметь отличать измерения, содержащие грубые ошибки, от измерений, подверженных лишь случайным ошибкам di. Для случая, когда di независимы и имеют одинаковое нормальное распределение, наиболее совершенный способ выявления измерений, содержащих грубые ошибки, предложен Н. В. Смирновым.
Билет 41 - Виды выборок В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора. В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки: · собственно случайную; · механическую; · типическую (стратифицир
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.011 с.) |






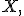 принимающей целочисленные значения
принимающей целочисленные значения  с вероятностями:
с вероятностями:  Данное распределение характеризуется двумя параметрами: целым числом n>0 называемым числом испытаний, и вещественным числом p, 0 ≤ p ≤ 1 называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из n независимых испытаний, в каждом из которых может произойти "успех" с вероятностью p, то случайная величина, равная числу успехов во всей серии, имеет указанное распределение.
Данное распределение характеризуется двумя параметрами: целым числом n>0 называемым числом испытаний, и вещественным числом p, 0 ≤ p ≤ 1 называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из n независимых испытаний, в каждом из которых может произойти "успех" с вероятностью p, то случайная величина, равная числу успехов во всей серии, имеет указанное распределение.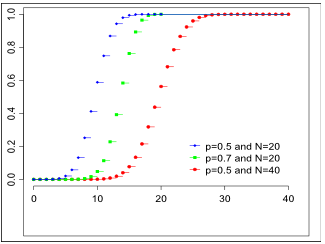 Функция вероятности Функция распределения
Функция вероятности Функция распределения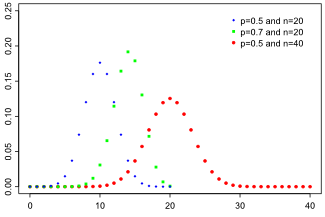
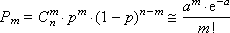 .
.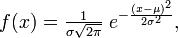 где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:


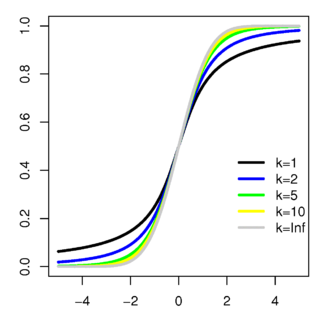 Плотность вероятности
Плотность вероятности 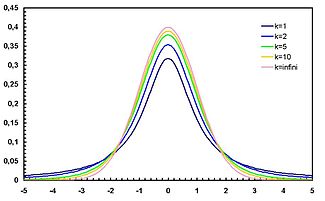 Функция распределения
Функция распределения
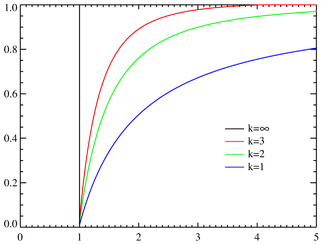

 где
где  — коэффициент регрессии,
— коэффициент регрессии,  — среднеквадратическое отклонение соответствующего факторного признака[12].
— среднеквадратическое отклонение соответствующего факторного признака[12]. (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
(тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена). ,
, .
.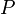 — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.
— суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y. — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)
— суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)



 — число связанных рангов в ряду X и Y соответственно.
— число связанных рангов в ряду X и Y соответственно. и вычисляется коэффициент корреляции Спирмена:
и вычисляется коэффициент корреляции Спирмена:



 — число групп, которые ранжируются.
— число групп, которые ранжируются. — число переменных.
— число переменных. — ранг
— ранг  -фактора у
-фактора у  -единицы.
-единицы.

 , то гипотеза об отсутствии связи отвергается.
, то гипотеза об отсутствии связи отвергается.

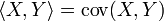 , то норма случайной величины будет равна
, то норма случайной величины будет равна  , и следствием неравенства Коши — Буняковского будет:
, и следствием неравенства Коши — Буняковского будет: .
. тогда и только тогда, когда
тогда и только тогда, когда  и
и 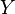 линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин): ,
, . Более того в этом случае знаки
. Более того в этом случае знаки  и
и 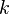 совпадают:
совпадают: .
. независимые случайные величины, то
независимые случайные величины, то  . Обратное в общем случае неверно.
. Обратное в общем случае неверно.



 аз. систематической ошибкой, а разности d1-b,...,dn-b - случайными ошибками. Таким образом, отсутствие систематич. ошибки означает, что b=0 и в этой ситуации d1,..., dn суть случайные ошибки. Величину
аз. систематической ошибкой, а разности d1-b,...,dn-b - случайными ошибками. Таким образом, отсутствие систематич. ошибки означает, что b=0 и в этой ситуации d1,..., dn суть случайные ошибки. Величину  , где s - квадратичное отклонение, наз. мерой точности (при наличии систематич. ошибки мера точности выражается отношением
, где s - квадратичное отклонение, наз. мерой точности (при наличии систематич. ошибки мера точности выражается отношением  . Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерении. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для нек-рых отдельных измерений. В качестве оценки неизвестной величины и обычно берут арифметич. среднее из результатов измерений
. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерении. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для нек-рых отдельных измерений. В качестве оценки неизвестной величины и обычно берут арифметич. среднее из результатов измерений

 в качестве оценки для m основан на том, что при достаточно большом числе га равноточных измерений, лишенных систематич. ошибки, оценки
в качестве оценки для m основан на том, что при достаточно большом числе га равноточных измерений, лишенных систематич. ошибки, оценки 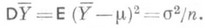
 . Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
. Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
 , то есть s2- несмещенная оценка для s2). Если случайные ошибки di имеют нормальное распределение, то отношение
, то есть s2- несмещенная оценка для s2). Если случайные ошибки di имеют нормальное распределение, то отношение

 . Можно показать, что относительная погрешность не будет превышать числа qс вероятностью
. Можно показать, что относительная погрешность не будет превышать числа qс вероятностью




