
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 46 – Линейная парная регрессияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Начало можно взять в билете №45 Линейная регрессия — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной y от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) x с линейной функцией зависимости. Модель линейной регрессии является часто используемой и наиболее изученной в эконометрике. А именно изучены свойства оценок параметров, получаемых различными методами при тех или иных предположениях о вероятностных характеристиках факторов и случайных ошибок модели. Предельные (асимптотические) свойства оценок нелинейных моделей также выводятся исходя из аппроксимации последних линейными моделями. Необходимо отметить, что с эконометрической точки зрения более важное значение имеет линейность по параметрам, чем линейность по факторам модели.
Коэффициенты линейной регрессии показывают скорость изменения зависимой переменной по данному фактору, при фиксированных остальных факторах (в линейной модели эта скорость постоянна):
Параметр b0, при котором нет факторов, называют часто константой. Формально - это значение функции при нулевом значении всех факторов. Для аналитических целей удобно считать, что константа - это параметр при "факторе", равном 1 (или другой произвольной постоянной, поэтому константой называют также и этот "фактор"). В таком случае, если перенумеровать факторы и параметры исходной модели с учетом этого (оставив обозначение общего количества факторов - k), то линейную функцию регрессии можно записать в следующем виде, формально не содержащем константу:
Линейная модель может быть как с константой, так и без константы. Тогда в этом представлении первый фактор либо равен единице, либо является обычным фактором соответственно. Парная и множественная регрессия В частном случае, когда фактор единственный (без учета константы), говорят о парной или простейшей линейной регрессии: Когда количество факторов (без учета константы) больше 1-го, то говорят о множественной регрессии. Линейная парная регрессия Связь зависимой переменной с одной или несколькими независимыми переменными описывается с помощью уравнения регрессии: = f(x1, x2,..., xm). Это уравнение показывает, каково будет в среднем значение y, если переменные x примут конкретные значения. Если независимая переменная одна, то регрессия называется парной. Построение уравнения регрессии включает два этапа: 1) определение вида зависимости (этап спецификации); 2) определение коэффициентов регрессии (этап идентификации). Предположим, на этапе спецификации установлено, что между величинами x и y существует линейная зависимость. Реальные значения y будут отличаться от этой теоретической зависимости. В общем случае линейное уравнение связи двух переменных, учитывающее случайные отклонения, можно представить в виде: где
В уравнении (6.1) можно выделить две части: систематическую, случайную ( Коэффициенты где n - объем выборки. Обозначим через ei отклонение реального значения отклика yi от теоретически рассчитанного по уравнению i. Параметры a и b уравнения регрессии чаще всего оцениваются с помощью метода наименьших квадратов (МНК). Суть его состоит в том, чтобы зная положение точек на плоскости XY, так провести линию регрессии, чтобы сумма квадратов отклонений ei2 этих точек от проведенной прямой вдоль оси OY была минимальной. Математически критерий оценки параметров линейной парной регрессии записывается так: Условие существования экстремума функции – равенство нулю производной: Раскрыв скобки и выполнив преобразования, получим систему из двух уравнений с двумя неизвестными: Разделив первое уравнение на n, получим: т.е. метод наименьших квадратов дает прямую, проходящую через точку Решая систему, получим расчетные формулы для нахождения коэффициентов уравнения регрессии:
Заметим, что данные значения могут быть легко получены средствами пакета Microsoft Excel. Для вычисления коэффициента a используется функция ОТРЕЗОК, коэффициента b – функция НАКЛОН.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.006 с.) |





 , (6.1)
, (6.1) – отклонение от теоретически предполагаемого значения;
– отклонение от теоретически предполагаемого значения; и
и  - неизвестные параметры (коэффициенты регрессии).
- неизвестные параметры (коэффициенты регрессии).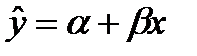 , где
, где 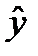 характеризует некоторое среднее значение y для данного значения x;
характеризует некоторое среднее значение y для данного значения x; ).
). , (6.2)
, (6.2)


 ,
, .
. (6.3)
(6.3)



