
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляция, частная корреляция, регрессияСодержание книги
Поиск на нашем сайте
При анализе связи между переменными, измеренными на интервальном уровне, часто используют графическое представление такой связи, называемое диаграммой рассеивания. На диаграмме рассеивания каждое наблюдение, т. е. каждый «случай», изображается точкой в двухмерной системе координат. Значение независимой переменной для данного наблюдения определяет положение соответствующей точки относительно оси X, а значение зависимой переменной задает вторую координату точки — по оси Y. Иными словами, перпендикуляр, опущенный из точки-«случая» на ось X, соответствует измеренному уровню независимой переменной, тогда как перпендикуляр, опущенный на ось Y, будет точно соответствовать наблюдавшемуся уровню зависимой переменной. Пусть, например, мы располагаем данными о бюджетах 10 партий и о числе полученных этими партиями мест в парламенте. Исходя из гипотезы о влиянии размера партийного бюджета (X) на полученное в результате выборов число депутатских мандатов (Y), мы можем построить диаграмму рассеивания, подобную изображенной на рисунке 21.
Рис. 21. Диаграмма рассеивания, отражающая связь величины партийного бюджета в млн. руб. (X) с количеством мест в парламенте (Y) для 10 политических партий
Каждая точка на рисунке соответствует одной из десяти партий. Невзирая на некоторые «аномальные» случаи, подобные обведенным кружками, диаграмма довольно ясно показывает, что всякое приращение в размерах партийной кассы (сдвиг вправо по оси Х) влечет за собой увеличение парламентского представительства (сдвиг вверх по оси ординат). Между переменными X и Y существует линейное отношение: если одна переменная возрастает по величине, то это же происходит и с другой. Помимо указания на природу отношения двух переменных, диаграмма на рисунке 21 позволяет также сделать некоторые предположения об интенсивности, силе этого отношения. Очевидно, что чем более компактно, «скученно» располагаются точки-наблюдения вокруг пунктирной прямой линии (описывающей идеальное линейное отношение X и Y), тем сильнее зависимость. На рисунке 22 приведены еще три диаграммы рассеивания.
Рис. 22. Диаграммы рассеивания для гипотетических данных
Очевидно, что на рисунке 22а какая-либо связь между X и Y попросту отсутствует. На рисунке 226 воображаемая прямая линия (отмечена пунктиром) пересекла бы диаграмму сверху вниз, из левого верхнего в правый нижний угол. Иными словами, линейная связь в этом случае имеет обратное направление: чем больше X, тем меньше зависимая переменная Y. Заметим также, что «кучность» расположения точек вдоль воображаемой прямой на рисунке 226 не очень велика, а значит и связь (корреляция) между переменными не только обратная, отрицательная, но еще и не очень сильная, умеренная. Наконец, на рисунке 22в зависимую и независимую переменную связывает явно нелинейное отношение: воображаемый график нисколько не похож на прямую линию и напоминает скорее параболу[38]. Отметим, что методы анализа, о которых сейчас пойдет речь, не годятся для этого нелинейного случая, так как обычная формула для подсчета коэффициента корреляции даст нулевое значение, хотя связь между переменными существует. Существует обобщенный показатель, позволяющий оценить, насколько связь между переменными приближается к линейному функциональному отношению, которое на диаграмме рассеивания выглядит как прямая линия. Это коэффициент корреляции, измеряющий тесноту связи между переменными, т. е. их тенденцию изменяться совместно. Как и в рассмотренных выше мерах связи качественных признаков, коэффициент корреляции позволяет оценить возможность предсказания значений зависимой переменной по значениям независимой. Общая формула для вычисления коэффициента корреляции Пирсона включает в себя величину ковариации значений X и Y. Эта величина (S xy) характеризует совместное изменение значений двух переменных. Она задается как сумма произведений отклонений наблюдаемых значений X и Y от средних Наконец, при отсутствии систематической связи произведения будут иногда положительными, иногда отрицательными, а их сумма (и, следовательно, ковариация Х и Y) будет, в пределе, равная нулю. Таким образом, ковариация показывает величину и направление связи, совместного изменения Х и Y. Если разделить ковариацию S xy на стандартные отклонения S x и S y (чтобы избавиться от влияния масштаба шкал, в которых измеряются Х и Y), то мы получим искомую форму коэффициента корреляции Пирсона (r xy):
Более удобная для практических вычислений расчетная формула выглядит так:
Несмотря на несколько устрашающий вид, расчетная формула очень проста. Для «ручного» вычисления r хувам понадобятся лишь пять величин: суммы значений по Х и Y Просуммировав значения в столбцах, мы получим Величина, которая равна квадрату коэффициента корреляции Пирсона, т. е. r2, имеет ряд интересных статистических свойств. Отметим сейчас, что r2 является ПУО-мерой связи, подобной обсуждавшимся выше. Можно показать, что она характеризует ту долю дисперсии значений Y, которая объясняется наличием корреляции между Х и Y. (Естественно, величина r 2 будет всегда положительной и не может превзойти по абсолютной величине коэффициент корреляции)[40]. Та часть разброса в значениях Y, которая не может быть предсказана по значениям X,— это дисперсия ошибки нашего прогноза, т. е. 1 - r2. Необъясненный разброс в значениях Y присутствует в том случае, когда при равных уровнях X (ср., например, дневные температуры в Варшаве и Бонне из таблицы 8.11) сохраняются различия в значениях Y. Таблица 8.11 Максимальные дневные и ночные температуры воздуха в некоторых городах
Коэффициент корреляции позволяет оценить степень связи между переменными. Однако этого недостаточно для того, чтобы непосредственно преобразовывать информацию, относящуюся к одной переменной, в оценки другой переменной. Допустим, мы выяснили, что коэффициент корреляции между переменными «величина партийного бюджета» и «число мест в парламенте» равен 0,8. Можем ли мы теперь предсказать, сколько мест в парламенте получит партия, годовой бюджет которой равен 100 млн. рублей? Похоже, что знание величины коэффициента корреляции нам здесь не поможет. Однако мы можем вспомнить, что коэффициент корреляции — это еще и оценка соответствия разброса наших наблюдений той идеальной модели линейного функционального отношения, которое на рассмотренных выше диаграммах рассеивания (см. рис. 21—22) представлено пунктирными прямыми. Эти линии называют линиями регрессии. Если бы все наблюдения аккуратно «укладывались» на линию регрессии, то для предсказания значения зависимой переменной достаточно было бы восстановить перпендикуляр к оси Y из той точки прямой, которая соответствует известному значению X. На рисунке 23 показано, как можно было бы графически определить ожидаемые значения Y для гипотетического примера с партийной кассой и местами в парламенте. (Разумеется, найти искомое значение Y можно и без линейки, с помощью вычислений, если известен угол наклона регрессионной прямой и точка пересечения с осью ординат).
Рис. 23. Предсказание значения Y по значению Х для гипотетических данных
Как говорилось выше, линия регрессии не обязательно должна быть прямой, но мы ограничимся рассмотрением самого простого случая линейной зависимости (нелинейные связи во многих случаях также могут быть приближенно описаны линейными отношениями). Существуют специальные статистические процедуры, которые позволяют найти регрессионную прямую, максимально соответствующую реальным данным. Регрессионный анализ, таким образом, дает возможность предсказывать значения Y по значениям X с минимальным количеством ошибок. В общем виде уравнение, описывающее прямую линию регрессии Y по X, выглядит так:
где Социологи обычно осуществляют регрессионный анализ, используя возможности распространенных прикладных пакетов компьютерных программ (например, SPSS). В этом случае для нахождения линии регрессии, лучше всего соответствующей данной выборке наблюдений, которая представлена точками на диаграмме рассеивания, используют метод минимизации взвешенной суммы квадратов расстояний между этими точками и искомой прямой[41]. Хотя здесь не место для обсуждения статистических деталей, мы все же сделаем несколько замечаний, относящихся к осмысленному (или бессмысленному) использованию техники линейной регрессии. Во-первых, как и в ранее обсуждавшихся примерах анализа связи, наличие координации, согласованности в изменениях двух переменных еще не доказывает, что обнаруженное отношение носит собственно каузальный характер. Проверка альтернативных причинных моделей, иначе объясняющих эмпирическую сопряженность переменных-признаков, может основываться только на содержательных теоретических представлениях. Далее, нужно помнить о том, что регрессионные коэффициенты в общем случае асимметричны. Если мы решим, что это Y, а не X является независимой переменной, то вполне можем рассчитать другую по величине пару коэффициентов — аху и bху. (Заметьте, что порядок букв в подстрочном индексе значим: первой всегда идет предсказываемая переменная, а второй — предсказывающая.) Разумеется, при выборе кандидатов в зависимые и независимые переменные такжеважны не статистические, а содержательные соображения. Если вернуться к затронутой выше взаимосвязи между линейной регрессией и корреляцией, то здесь мы можем сделать следующие дополнения. Пусть все точки-наблюдения аккуратно размещены на регрессионной прямой. Перед нами почти невероятный случай абсолютной линейной зависимости. Зная, например, что коэффициент b (нестандартизованный) равен 313, мы можем утверждать, что именно такова величина воздействия переменной X на зависимую переменную Y. Кроме того, мы можем точно сказать, что единичная прибавка в величине X вызовет увеличение Y на ту же величину, 313 (если, допустим, X — стаж работы, а Y — зарплата, то с увеличением стажа на год зарплата растет на 313 рублей). В этом случае коэффициент корреляции будет равен в точности 1,0, что свидетельствует о сильном, «абсолютном», характере связи переменных. Различие между предсказанными и наблюдаемыми значениями в этом случае отсутствует. Корреляция как мера точности прогноза показывает, что ошибок предсказания просто нет. В действительности, однако, из-завлияния других переменных и случайной выборочной ошибки точки-наблюдения обычно лежат выше или ниже прямой, которая, как говорилось, являетсялишь наилучшим приближением реальных данных. Коэффициент корреляции Пирсона r и величина r 2 по-прежнему служат оценкой точности прогноза, основанного на линии регрессии. Вполне возможны ситуации, когда коэффициент регрессии очень велик, воздействие X на Y просто громадно, но корреляция низка и, следовательно, точность прогноза невелика. Нет ничего необычного и в обратной ситуации: воздействие X на Y относительно мало, а коэффициент корреляции и объясненная дисперсия очень велики. Посмотрев на приведенные выше диаграммы рассеивания, можно легко уяснить себе смысл отношения между корреляцией и регрессией: первая имеет прямое отношение к «разбросанности» точек наблюдения (чем выше «разбросанность», тем ниже r2 и ненадежнее прогноз), тогда как коэффициент регрессии описывает наклон, «крутизну» линии. Однако существующее здесь различие не стоит и преувеличивать: регрессионный коэффициент (наклон прямой) для стандартизованных данных в точности равен коэффициенту корреляции Пирсона r [42]. Предположим, что исследователь изучает зависимость между образованием матери (X) и образованием детей (Y). Обе переменные измерены как количество лет, затраченных на получение образования. Найдя достаточно высокую корреляцию между X и Y — скажем, равную 0,71, — он также находит коэффициенты регрессии а и b и устанавливает, что r 2 (называемый также коэффициентом детерминации) в данном случае приближенно равен 0,5. Это значит, что доля вариации в значениях переменной Y (образование детей), объясненная воздействием переменной-предиктора X (материнское образование), составляет около 50% общей дисперсии предсказываемой переменной. Коэффициент корреляции между переменными достаточно велик и статистически значим даже для не очень большой выборки. Следовательно, обнаруженная взаимосвязь переменных не может быть объяснена случайными погрешностями выборки. В пользу предложенной исследователем причинной гипотезы говорит и то обстоятельство, что альтернативная гипотеза — образование детей влияет на образовательный статус родителей — крайне неправдоподобна и может быть отвергнута на основании содержательных представлений о временной упорядоченности событий. Однако все еще не исключены те возможности, которые мы обсуждали в параграфе, посвященном методу уточнения. Иными словами, нам следует считаться с вероятностью того, что какая-то другая переменная (или несколько переменных) определяют и образование родителей и образование детей (например, финансовые возможности либо интеллект). Чтобы проверить такую конкурирующую гипотезу, следует рассчитать так называемую частную корреляцию. Логика расчета частной корреляции совпадает с логикой построения частных таблиц сопряженности при использовании метода уточнения. Построить частные таблицы сопряженности для различных уровней контрольной переменной в случае, когда переменные измерены на интервальном уровне, — это практически неразрешимая задача. Чтобы убедиться в этом, достаточно подсчитать, каким должно быть количество таблиц уже при десяти-двенадцати категориях каждой переменной. Расчет коэффициента частной корреляции — это простейшее средство уточнения исходной причинной модели при введении дополнительной переменной. Интерпретация коэффициента частной корреляции не отличается от интерпретации частных таблиц сопряженности: частной корреляцией называют корреляцию между двумя переменными, когда статистически контролируется, или «поддерживается на постоянном уровне», третья переменная (набор переменных). Если, предположим, при изучении корреляции между образованием и доходом нам понадобится «вычесть» из полученной величины эффект интеллекта, предположительно влияющего и на образование, и на доход, достаточно воспользоваться процедурой вычисления частной корреляции. Полученная величина будет свидетельствовать о чистом влиянии образования на доход, из которого «вычтена» линейная зависимость образования от интеллекта. Мюллер и соавторы[43] приводят интересный пример использования коэффициента частной корреляции. В исследовании П. Риттербэнда и Р. Силберстайна изучались студенческие беспорядки 1968—1969 гг. Одна из гипотез заключалась в том, что число нарушений дисциплины и демонстраций протеста в старших классах учебных заведений связано с различиями показателей академической успеваемости учащихся. Корреляция между частотой «политических» беспорядков и средней успеваемостью оказалась отрицательной (хуже успеваемость — больше беспорядков) и статистически значимой (r = -0,36). Однако еще более высокой была корреляция между частотой беспорядков и долей чернокожих учащихся (r = 0,54). Исследователи решили проверить, сохранится ли связь между беспорядками и успеваемостью, если статистически проконтролировать влияние расового состава учащихся. Коэффициент частной корреляции частоты беспорядков и успеваемости при контроле расового состава учащихся оказался равным нулю. Исходная корреляция между беспорядками и успеваемостью в данном случае может быть описана причинной моделью «ложной взаимосвязи» (см. рис. 19): наблюдаемые значения этих двух переменных скоррелированы лишь потому, что обе они зависят от третьей переменной — доли чернокожих в общем количестве учащихся. Чернокожие студенты, как заметили исследователи, оказались восприимчивее к предложенным самыми активными «политиканами» образцам участия в политических беспорядках. Кроме того, их успеваемость, помимо всяких политических событий, была устойчиво ниже, чем средняя успеваемость белых. Коэффициент частной корреляции между переменными X и Y при контроле дополнительной переменной Z (т. е. при поддержании Z «на постоянном уровне») обозначают как rхy.z. Для его вычисления достаточно знать величины наблюдаемых попарных корреляций между переменными X, Y и Z (n. e. простых корреляций — r xy, ryz, r xz):
Как всякая выборочная статистика, коэффициент корреляции подвержен выборочному разбросу. Существует некоторая вероятность того, что для данной выборки будет получено ненулевое значение коэффициента корреляции, тогда как истинное его значение для генеральной совокупности равно нулю. Иными словами, существует задача оценки значимости полученных значений корреляций и коэффициентов регрессии, относящаяся к области теории статистического вывода. Описание соответствующих статистических методов выходит за рамки этой книги, поэтому мы рассмотрим лишь самые общие принципы, позволяющие решать описанную задачу в простых случаях и интерпретировать соответствующие показатели при использовании стандартных компьютерных программ. Прежде всего вероятностная оценка коэффициента корреляции подразумевает оценку отношения к его случайной ошибке. Удобная, хотя и не вполне надежная формула для вычисления ошибки коэффициента корреляции (m r) выглядит так[44]:
Всегда полезно вычислить отношение полученной величины r к его ошибке (т. е. r/тr). В использовавшемся нами примере данных о погоде коэффициент корреляции оказался равен 0,91, а его выборочная ошибка составляет:
Отношение r к тr обозначаемое как t, составит Когда значение r не столь близко к единице и выборка невелика, нужно все же проверить статистическую гипотезу о равенстве r нулю в генеральной совокупности. Для этого нужно определить t по формуле:
где t — это величина так называемого t-критерия Стьюдента (см. также главу 4), r — выборочный коэффициент корреляции, п — объем выборки. Для установления значимости вычисленной величины t-критерия пользуются таблицами t-распределения для (n - 2) степеней свободы (см. табл. 4.1). Во многих пособиях по статистике можно найти и готовые таблицы критических значений коэффициента корреляции r для данного уровня значимости a. В этом случае отпадает необходимость в каких-либо вычислениях t: достаточно сравнить полученную величину коэффициента корреляции с табличным значением[45]. (Например, величина коэффициента корреляции r = 0,55 будет существенной на уровне значимости р = 0,01 даже для выборки объемом 105, так как критическое значение составляет 0,254.)
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.144 (0.015 с.) |



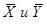 соответственно, т. е.
соответственно, т. е.  деленная на количество наблюдений. Чтобы понять «физический смысл» ковариации, достаточно обратить внимание на следующее свойство: если для какого-то объекта i в выборке оба значения ¾ C i и U i ¾ окажутся высокими, то и произведение
деленная на количество наблюдений. Чтобы понять «физический смысл» ковариации, достаточно обратить внимание на следующее свойство: если для какого-то объекта i в выборке оба значения ¾ C i и U i ¾ окажутся высокими, то и произведение  на
на  будет большим и положительным. Если оба значения (по Х и по Y) низки, то произведение двух отклонений, т.е. двух отрицательных чисел, также будет положительным. Таким образом, если линейная связь Х и Y положительная и велика, сумма таких произведений для всех наблюдений также будет положительна. Если связь межу Х и Y обратная, то многим положительным отклонениям по Х будет соответствовать отрицательные отклонения по Y, т.е. сумма отрицательных произведений отклонений будет отрицательной.
будет большим и положительным. Если оба значения (по Х и по Y) низки, то произведение двух отклонений, т.е. двух отрицательных чисел, также будет положительным. Таким образом, если линейная связь Х и Y положительная и велика, сумма таких произведений для всех наблюдений также будет положительна. Если связь межу Х и Y обратная, то многим положительным отклонениям по Х будет соответствовать отрицательные отклонения по Y, т.е. сумма отрицательных произведений отклонений будет отрицательной.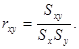

 суммы квадратов значений по X и Y
суммы квадратов значений по X и Y  суммы произведений Х и Y по всем объектам-«случаям»
суммы произведений Х и Y по всем объектам-«случаям» 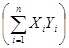 . В таблице 8. 11 приведены данные о максимальных дневных и ночных температурах, зарегистрированных в 10 городах[39].
. В таблице 8. 11 приведены данные о максимальных дневных и ночных температурах, зарегистрированных в 10 городах[39]. и
и  Возведя каждое из значений X и Y в квадрат и просуммировав, мы найдем, что
Возведя каждое из значений X и Y в квадрат и просуммировав, мы найдем, что  и
и  Сумма попарных произведений Xi и Yi.
Сумма попарных произведений Xi и Yi. 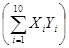 составит 4359. Вы можете самостоятельно убедиться в том, что подстановка всех значений в расчетную формулу даст (надеюсь) величину r xy = 0,91. Иными словами, корреляция между дневными и ночными температурами воздуха очень высока, но все же отлична от 1,0 (коэффициент корреляции может меняться в пределах от -1,0 до +1,0). Это отличие, вероятно, объясняется влиянием других факторов (продолжительность дня и ночи, облачность, географическое положение и т. п.). Судя по полученной величине корреляции, знание дневных температур позволяет предсказывать ночные температуры с очень высокой точностью, но не безошибочно.
составит 4359. Вы можете самостоятельно убедиться в том, что подстановка всех значений в расчетную формулу даст (надеюсь) величину r xy = 0,91. Иными словами, корреляция между дневными и ночными температурами воздуха очень высока, но все же отлична от 1,0 (коэффициент корреляции может меняться в пределах от -1,0 до +1,0). Это отличие, вероятно, объясняется влиянием других факторов (продолжительность дня и ночи, облачность, географическое положение и т. п.). Судя по полученной величине корреляции, знание дневных температур позволяет предсказывать ночные температуры с очень высокой точностью, но не безошибочно.

 — то предсказываемое значение по переменной Y (в только что рассмотренном примере — количество мест в парламенте), а — это точка, в которой прямая пересекает ось Y (т. е. значение Y для случая, когда Х = 0), и b — коэффициент регрессии, т. е. наклон прямой. Часто удобно измерять обе переменные не в «сырых» шкалах, а в единицах отклонения от среднего. Процедура стандартизации, т. е. перевода исходной шкалы в стандартные Z-оценки, вам уже известна. Преимущество использования стандартизированных переменных в регрессионном анализе заключается в том, что линия регрессии в этом случае проходит через начало координат. Стандартизованный коэффициент регрессии (наклон прямой) обозначают обычно греческой буквой b (либо лат. b *). Правда, в отличие от b -коэффициента, b не позволяет прямо заключить, на какое количество исходных единиц возрастет Y при увеличении X на одну единицу (например, насколько увеличится число депутатских мандатов при увеличении бюджета на 1 млн. рублей или насколько увеличивается заработная плата при увеличении стажа работы на один год). С другой стороны, b позволяет сопоставить влияние на независимую переменную контрольных переменных, измеренных в разных шкалах.
— то предсказываемое значение по переменной Y (в только что рассмотренном примере — количество мест в парламенте), а — это точка, в которой прямая пересекает ось Y (т. е. значение Y для случая, когда Х = 0), и b — коэффициент регрессии, т. е. наклон прямой. Часто удобно измерять обе переменные не в «сырых» шкалах, а в единицах отклонения от среднего. Процедура стандартизации, т. е. перевода исходной шкалы в стандартные Z-оценки, вам уже известна. Преимущество использования стандартизированных переменных в регрессионном анализе заключается в том, что линия регрессии в этом случае проходит через начало координат. Стандартизованный коэффициент регрессии (наклон прямой) обозначают обычно греческой буквой b (либо лат. b *). Правда, в отличие от b -коэффициента, b не позволяет прямо заключить, на какое количество исходных единиц возрастет Y при увеличении X на одну единицу (например, насколько увеличится число депутатских мандатов при увеличении бюджета на 1 млн. рублей или насколько увеличивается заработная плата при увеличении стажа работы на один год). С другой стороны, b позволяет сопоставить влияние на независимую переменную контрольных переменных, измеренных в разных шкалах.


 Разумеется, коэффициент, превосходящий свою случайную ошибку почти в 16 раз, может быть признан значимым даже без построения доверительных интервалов.
Разумеется, коэффициент, превосходящий свою случайную ошибку почти в 16 раз, может быть признан значимым даже без построения доверительных интервалов.



