
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ связи между двумя переменнымиСодержание книги
Поиск на нашем сайте
Хотя результаты одномерного анализа данных часто имеют самостоятельное значение, большинство исследователей уделяют основное внимание анализу связей между переменными. Самым простым и типичным является случай анализа взаимосвязи (сопряженности) двух переменных. Используемые здесь методы задают некоторый логический каркас, остающийся почти неизменным и при рассмотрении более сложных моделей, включающих множество переменных. Устойчивый интерес социологов к двумерному и многомерному анализу данных объясняется вполне понятным желанием проверить гипотезы о причинной зависимости двух и более переменных. Ведь утверждения о причинных взаимосвязях составляют фундамент не только социальной теории, но и социальной политики (по крайней мере, так принято считать). Так как возможности социологов проверять причинные гипотезы с помощью эксперимента, как уже говорилось, ограниченны, основной альтернативой является статистический анализ неэкспериментальных данных. В общем случае для демонстрации причинно-следственного отношения между двумя переменными, скажем, X и Y, необходимо выполнить следующие требования: 1) показать, что существует эмпирическая взаимосвязь между переменными; 2) исключить возможность обратного влияния Y на Х; 3) убедиться, что взаимосвязь между переменными не может быть объяснена зависимостью этих переменных от какой-то дополнительной переменной (или переменных). Первым шагом к анализу взаимоотношений двух переменных является их перекрестная классификация, или построение таблицы сопряженности. Речь идет о таблице, содержащей информацию о совместном распределении переменных. Допустим, в результате одномерного анализа данных мы установили, что люди сильно различаются по уровню заботы о своем здоровье: некоторые люди регулярно делают физические упражнения, другие — полностью пренебрегают зарядкой. Мы можем предположить, что причина этих различий — какая-то другая переменная, например, пол, образование, род занятий, доход и т. п. Пусть мы располагаем совокупностью данных о занятиях физзарядкой и образовании для выборки горожан. Для простоты мы предположим, что обе переменные имеют лишь два уровня: высокий и низкий. Так как данные об образовании исходно разбиты на большее количество категорий, нам придется их перегруппировать, разбив весь диапазон значений на два класса. Предположим, мы выберем в качестве граничного значения 10 лет обучения, так что люди, получившие неполное среднее и среднее образование, попадут в «низкую» градацию, а остальные — в «высокую». (Это, конечно, большое огрубление, но мы используем его из соображений простоты.) Для занятий физическими упражнениями мы соответственно воспользуемся двумя категориями — «делают физзарядку» и «не делают физзарядку». Таблица 8.3 показывает, как могло бы выглядеть совместное распределение этих двух переменных. Таблица 8.3 Взаимосвязь между уровнем образования и занятиями физкультурой
В таблице 8.3 два столбца (для образования) и две строки (для занятий физкультурой), следовательно, размерность этой таблицы 2x2. Кроме того, имеются дополнительные крайний столбец и крайняя строка (маргиналы таблицы), указывающие общее количество наблюдений в данной строке или в столбце. В правом нижнем углу указана общая сумма, т. е. общее число наблюдений в выборке. Не давшие ответа уже исключены (для реальных данных их число также стоит указать, но не в таблице, а в подтабличной сноске). Заметим здесь, что многие исследователи при построении таких таблиц пользуются неписаным правилом: для той переменной, которую полагают независимой, отводится верхняя строка (горизонталь), а зависимую располагают «сбоку», по вертикали (разумеется, соблюдение этого правила не является обязательным и ничего с точки зрения анализа не меняет). Обычно характер взаимоотношений между переменными в небольшой таблице можно определить даже «на глазок», сравнивая числа в столбцах или строках. Еще легче это сделать, если вместо абсолютных значений стоят проценты. Чтобы перевести абсолютные частоты, указанные в клетках таблицы, в проценты, нужно разделить их на маргинальные частоты и умножить на 100. Если делить на маргинал столбца, мы получим процент по столбцу. Например, Так как вывод о наличии взаимосвязи между переменными требует демонстрации различий между подгруппами по уровню зависимой переменной, при анализе таблицы сопряженности можно руководствоваться простыми правилами. Во-первых, нужно определить независимую переменную и, в соответствии с принятым определением, пересчитать абсолютные частоты в проценты. Если независимая переменная расположена по горизонтали таблицы, мы считаем проценты по столбцу; если независимая переменная расположена по вертикали, проценты берутся от сумм по строке. Далее сравниваются процентные показатели, полученные для подгрупп с разным уровнем независимой переменной, каждый раз внутри одной категории зависимой переменной (например, внутри категории делающих зарядку). Обнаруженные различия свидетельствуют о существовании взаимосвязи между двумя переменными. (В качестве упражнения примените описанную процедуру к таблице 8.3, чтобы убедиться в наличии связи между уровнем образования и занятиями физкультурой.) Отметим специально, что элементарная таблица сопряженности размерности 2x2 — это минимально необходимое условие для вывода о наличии взаимосвязи двух переменных. Знания о распределении зависимой переменной недостаточно. Нельзя, например, утверждать, будто из того, что 75% детей-первенцев имеют интеллект выше среднего, а 25% — средний и более низкий, следует зависимость между порядком рождения и интеллектом. Необходимо проанализировать и распределение показателей интеллекта для детей-непервенцев. Варьировать должна не только зависимая, но и независимая переменная. Для таблиц размерности 2 х 2 и более можно рассчитать специальные показатели (статистики), дающие суммарное выражение степени взаимосвязи, ассоциации между двумя переменными. Таких мер связи довольно много. Для случая двух номинальных переменных существуют два основных подхода к подсчету коэффициентов взаимосвязи. Проанализировав их общую логику, мы получим возможность ориентироваться в многообразии конкретных показателей, предлагаемых прикладными программами анализа данных. Первый подход базируется на статистике, называемой «хи-квадрат». На ее основе можно рассчитать несколько коэффициентов взаимосвязи. Рассмотрим в качестве примера коэффициент «фи» (греч.j), формула для которого была впервые предложена сэром Карлом Пирсоном в 1901 году специально для того, чтобы сделать возможным анализ взаимосвязи между двумя переменными, измеренными на неколичественном уровне. Таблица 8.4
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

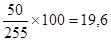 %, т. е. 19,6% имеющих низкий уровень образования делают зарядку (но не наоборот!). Если делить на маргинал строки, то мы получим другую величину — процент по строке. В частности, можно заметить, что 80% делающих зарядку, составляют люди с высоким уровнем образования
%, т. е. 19,6% имеющих низкий уровень образования делают зарядку (но не наоборот!). Если делить на маргинал строки, то мы получим другую величину — процент по строке. В частности, можно заметить, что 80% делающих зарядку, составляют люди с высоким уровнем образования  Деление на общую численность выборки дает общий процент. Так, всего в выборке 50% людей, делающих зарядку.
Деление на общую численность выборки дает общий процент. Так, всего в выборке 50% людей, делающих зарядку.


