
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Основные задачи анализа данных на компьютереСодержание книги
Поиск на нашем сайте
Анализ данных позволяют выявлять закономерности на фоне случайностей, делать обоснованные выводы и прогнозы, давать оценки вероятностей их выполнения или невыполнения. Вопрос. Случайные переменные и законы их распределения Каждая случайная величина задает распределение вероятностей на множестве своих значений. Если ξ — случайная величина, принимающая значения из X, то мы можем задать распределение вероятностей Pξ на X следующим образом: Pξ(A) = P(ξ ∈ A). Виды случайных величин. В практических задачах обычно используются два вида случайных величин — дискретные и непрерывные, хотя бывают и такие случайные величины, которые не являются ни дискретными, ни непрерывными. Дискретные случайные величины обладают тем свойством, что мы можем перечислить (перенумеровать) все их возможные значения. Таким образом, для задания распределения вероятностей, порожденных дискретными случайными величинами, надо только указать вероятности каждого возможного значения этой случайной величины. Определение. Случайную величину называют дискретной, если множество ее возможных значений конечно, либо счетно. Каждое возможное значение дискретной случайной величины имеет положительную вероятность (иногда, впрочем, допускают, что некоторые значения могут иметь нулевые вероятности, особенно когда рассматривают не одно, а несколько дискретных распределений одновременно). Функция распределения. Пусть ξ обозначает случайную величину, принимающую вещественные значения, x — вещественное число. Определение. Функцией распределения F(x) случайной величины ξ называют F(x) = P(ξ<= x). Ясно, что функция F(x) монотонно возрастает с ростом x. Непрерывные случайные величины. Определение. Случайную величину, принимающую вещественные значения, называют непрерывной, если непрерывна ее функция распределения. Непрерывным в этом случае называют и соответствующее распределение вероятностей. Плотность вероятности.(НСВ) Определение. Функция p(t) называется плотностью вероятности в точке t (иногда — плотностью случайной величины ξ ), если для любых чисел a, b (пусть a < b ) P(a < ξ < b) = Вопрос. Числовые характеристики распределения вероятностей
Начнем с так называемого первого момента случайной величины ξ, называемого также математическим ожиданием, или средним значением ξ. Его обозначают через Mξ или Eξ. Определение. Для дискретной случайной величины ξ со значениями x1, x2,..., имеющих вероятности p1, p2,... Mξ Определение. Для непрерывной случайной величины ξ с плотностью p(x), Mξ = причем интеграл должен сходиться абсолютно. Свойства математического ожидания. Перечислим без доказательства основные свойства математического ожидания. 1. Математическое ожидание постоянной равно этой постоянной. 2. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е. M(ξ + η) = Mξ + Mη. 3. Математическое ожидание произведения случайной величины на константу равно произведению этой константы на математическое ожидание случайной величины, т.е. Maξ = aMξ. Определение. Дисперсией Dξ случайной величины ξ называется величина Dξ = M(ξ − Mξ)2, или Dξ = Mξ2 − (Mξ)2. Дисперсия, так же как и математическое ожидание, существует не для всех случайных величин (не для всех распределений вероятностей). Если необходимо, чтобы показатель разброса случайной величины выражался в тех же единицах, что и значение этой случайной величины, то вместо Dξ используют величину средним квадратическим отклонением, или стандартным отклонением случайной величины ξ. Свойства дисперсии. Из свойств дисперсии отметим следующие: 1. Дисперсия постоянной равна нулю. 2. Для любой неслучайной постоянной a D(ξ + a) = D(ξ), D(aξ) = a2D(ξ). Определение. Квантилью xp случайной величины, имеющей функцию распределения F(x), называется решение xp уравнения F(x) = p. Медианой называется квантиль, соответствующая значению p = 0.5. Верхней квартилью называется квантиль, соответствующая значению p = 0.75. Нижней квартилью называется квантиль, соответствующая значению p = 0.25.
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.147 (0.01 с.) |



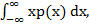
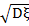 , которая называется
, которая называется


