Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 44 – Двухфакторный дисперсионный анализСодержание книги
Поиск на нашем сайте Начало можно взять из предыдущего билета №43 В двухфакторном дисперсионном анализе проверяется гипотеза о равенстве математических ожиданий выходного контролируемого параметра y при различных уровнях двух факторов. Например, производится выпуск одинаковых изделий различными предприятиями, использующих различных поставщиков. Здесь два фактора: предприятия и поставщики. Необходимо проверить гипотезу о равенстве математических ожиданий выходного контролируемого параметра (например качества изделия) при различных уровнях (предприятиях) первого и различных уровнях (поставщиках) второго фактора. Модель исследуемого объекта имеет вид:
В этой модели входные переменные x1 и x2 принимают дискретные значения, а выходная переменная y является непрерывной случайной величиной, вероятностная природа которой обусловлена наличием аддитивной помехи e. ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ БАЗИРУЕТСЯ НА СЛЕДУЮЩИХ ПРЕДПОСЫЛКАХ: 1. В каждом наблюдении ei имеет нормальное распределение с нулевым МО и конечной дисперсией. 2. Для любого i дисперсия ei является величиной постоянной. Рассмотрим вычислительную процедуру двухфакторного дисперсионного анализа. Пусть x1 принимает k различных значений или фактор x1 имеет k уровней, x2 принимает m различных значений или фактор x2 имеет m уровней. Пусть на каждом из сочетаний уровней имеется n наблюдений выходной величины y. Тогда результаты можно представить в виде таблицы:
Если уровни факторов x1 и x2 не оказывают влияние на математическое ожидание y, то все наблюдения представляют собой выборку из одной генеральной совокупности (при условии выполнения приведенных выше предпосылок). Тогда, дисперсию генеральной совокупности можно оценить следующими независимыми оценками: через средние значения y для каждого из уровней факторов x1 или x2 или как среднее арифметическое оценок дисперсий y для каждого из уровней x1 или x2. Как и в однофакторном дисперсионном анализе первая оценка называется оценкой дисперсии уровней S2ур, вторая - оценкой дисперсии ошибки S2ош. Для первого и второго факторов имеем:
где: где: y.j. - среднее по j-му уровню первого фактора, yi.. - среднее по j-му уровню второго фактора, y... - общее среднее. Оценка дисперсии ошибки вычисляется по формуле: где: yij. - среднее значение y при j-м уровне первого фактора Если влияние уровней факторов x1 и на x2 математическое ожидание отсутствует, то отношения F1 = S2ур1/S2ош, F2 = S2ур2/S2ош и Fвз = S2вз/S2ош подчинены закону распределения Фишера. Характеристики этого распределения зависят от числа степеней свободы оценок S2ур1, S2ур2, S2вз и S2ош (числа степеней свободы числителя ν1=(k-1), ν2=(m-1), νвз=(m-1)*(k-1) и знаменателя νош=m*k*(n-1)). Для любого заданного уровня значимости α всегда существует критическое значение Fкр, превысить которое F при отсутствии влияния уровней факторов x1, x2 и их взаимодействия x1*x2 может с вероятностью не более α. Это означает, что если в результате обработки данных расчетное значение F-статистики превысит соответствующее Fкр, то данные противоречат гипотезе о равенстве математических ожиданий y для всех уровней факторов x1, x2 и их взаимодействия x1*x2. Если F<Fкр, то данные не противоречат этой гипотезе, и следует считать, что уровни не оказывают влияние на математическое ожидание y. Билет 45 – Регрессия Регрессия, в теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости y=f(x), когда каждому значению независимой переменной x соответствует одно определённое значение величины y, при регрессионной связи одному и тому же значению x могут соответствовать в зависимости от случая различные значения величины y. Если при каждом значении x=xi наблюдается ni значений yi1…yin1 величины y, то зависимость средних арифметических Этот термин в статистике впервые был использован Френсисом Гальтоном (1886) в связи с исследованием вопросов наследования физических характеристик человека. В качестве одной из характеристик был взят рост человека; при этом было обнаружено, что в целом сыновья высоких отцов, что не удивительно, оказались более высокими, чем сыновья отцов с низким ростом. Более интересным было то, что разброс в росте сыновей был меньшим, чем разброс в росте отцов. Так проявлялась тенденция возвращения роста сыновей к среднему, то есть «регресс». Этот факт был продемонстрирован вычислением среднего роста сыновей отцов, рост которых равен 56 дюймам, вычислением среднего роста сыновей отцов, рост которых равен 58 дюймам, и т. д. После этого результаты были изображены на плоскости, по оси ординат которой откладывались значения среднего роста сыновей, а по оси абсцисс — значения среднего роста отцов. Точки (приближённо) легли на прямую с положительным углом наклона меньше 45°; важно, что регрессия была линейной. Итак, допустим, имеется выборка из двумерного распределения пары случайных переменных (X, Y). Прямая линия в плоскости (x, y) была выборочным аналогом функции g(x)=E(Y|X=x). В теории вероятностей под термином «регрессия» и понимают эту функцию, которая есть не что иное как условное математическое ожидание случайной переменной Y при условии, что другая случайная переменная X приняла значение x. Если, например, пара (X, Y) имеет двумерное нормальное распределение с E(X)=μ1, E(Y)=μ2, var(X)=σ12, var(Y)=σ22, cor(X, Y)=ρ, то можно показать, что условное распределение Y при X=x также будет нормальным с математическим ожиданием, равным
В этом примере регрессия Y на X является линейной функцией. Если регрессия Y на X отлична от линейной, то приведённые уравнения суть линейная аппроксимация истинного уравнения регрессии. В общем случае регрессия одной случайной переменной на другую не обязательно будет линейной. Также не обязательно ограничиваться парой случайных переменных. Статистические проблемы регрессии связаны с определением общего вида уравнения регрессии, построением оценок неизвестных параметров, входящих в уравнение регрессии, и проверкой статистических гипотез о регрессии. Эти проблемы рассматриваются в рамках регрессионного анализа. Простым примером регрессии Y по X является зависимость между Y и X, которая выражается соотношением: Y=u(X)+ε, где u(x)=E(Y | X=x), а случайные величины X и ε независимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи y=u(x) между неслучайными величинами y и x. На практике обычно коэффициенты регрессии в уравнении y=u(x) неизвестны и их оценивают по экспериментальным данным.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |



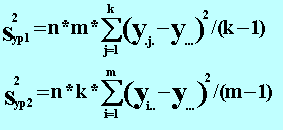
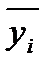 =(yi1+…+yin1)/ni от x=xi и является регрессией в статистическом понимании этого термина.
=(yi1+…+yin1)/ni от x=xi и является регрессией в статистическом понимании этого термина.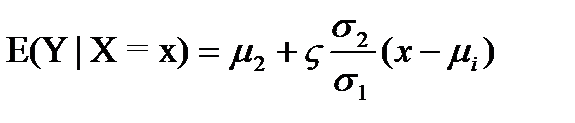 и дисперсией
и дисперсией