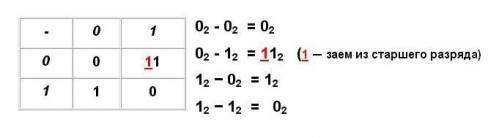Вопрос. Формы представления информации

Вопрос. Формы представления информации

Дискретная, или цифровая, форма. Для представления информации используется двоичная система счисления, в которой информация записывается с помощью нулей и единиц. Минимальной единицей информации является бит. Последовательность из восьми бит образуют байт. В современных компьютерах байт является минимальной адресуемой единицей информации. Это означает, что каждый байт имеет свой адрес.Числовая информация хранится в ЭВМ в двоичном коде, т.е. в виде последовательности нулей и единиц. Для представления чисел используются форматы с фиксированной запятой или с плавающей запятой, а также двоично-десятичный формат

Для представления текстовой, или символьной, информации используются кодовые таблицы. Каждому символу текста соответствует определенный двоичный код таблицы. Наиболее часто применяется ASCII (ASCII – AmericanStandardCodeforInformationInterchange – Американский стандартный код для обмена информацией). Каждому символу в коде ASCII соответствует двоичный код, соответствующий двоичному числу (от 0 до 255). ASCII является базой для современного стандарта кодирования символов Unicode.

Графическая информация может быть представлена в двух формах: растровой и векторной. Растровое изображение формируется из совокупности точек (пикселей). Качество изображения, определяемое количеством цветов и разрешением (количеством пикселей по горизонтали и вертикали) ограничивается только параметрами технических устройств. Для хранения информации одной точки может использоваться один, два (режим highcolor) или три байта (truecolor). Так как графическая информация в растровой форме требует больших объемов памяти, то для ее экономии используются форматы сжатого изображения:.gif,.jpg и др.

Для изображения графиков, чертежей, блок-схем используется векторная форма, при которой изображение формируется из линий, задаваемых их атрибутами (тип, цвет) и координатами их начала и конца.

Звуковая, или аудиоинформация представляет собой непрерывные колебания различной частоты и амплитуды. Для представления такой информации в цифровой ЭВМ ее необходимо перевести в дискретную форму, или оцифровать. В результате вместо плавной кривой получается ломаная кривая – квантованный сигнал по времени и по уровню. Чем ближе будет ломаная кривая к исходному колебанию, тем выше будет качество звука. Для записи значений квантованного сигнала по амплитуде используется один или два байта. Соответственно, в первом случае качество воспроизведения будет низким (динамический диапазон звукового сигнала не превысит 46 децибел), а во втором – высокое (96 децибел).

Существует другой способ записи звуковой информации – использование специальных команд MIDI, определяющих звучание отдельных нот. Этим способом пользуются для записи информации от музыкальных синтезаторов.

Видеоинформация в компьютере представляет собой последовательность быстро сменяющихся графических кадров. Качественное видеоизображение может быть обеспечено при частоте смены кадров не менее 25 Гц. Для хранения видеоинформации требуются значительные объемы памяти, поэтому используются специальные математические методы сжатия информации.

В настоящее время все большее применение находит мультимедийная форма представления информации, обеспечивающая сочетание звука, текста, видеоизображения и трехмерных объектов.

Вопрос Системы передачи информации

По виду сигналов, передаваемых в физической среде распростране­ния (линиях связи), системы передачи подразделяются на аналоговые и цифровые. В аналоговых системах сигналы, переносящие информацию по среде распространения, являются непрерывными функциями непре­рывного времени. В цифровых системах сигналы, переносящие инфор­мацию по среде распространения, являются дискретными функциями не­прерывного времени и представляют собой в большинстве случаев дво­ичные последовательности импульсов.

При этом входные сигналы системы передачи, содержащие полезную информацию, могут быть любого вида (например, аналоговые при переда­че голоса или дискретные при передаче данных).

В основе построения аналоговых систем передачи лежит принцип час­тотного уплотнения каналов, который называют также мультиплексиро­ванием с частотным разделением каналов. Этот принцип, в свою очередь, базируется на том, что ширина спектра передаваемых сигналов обычно существенно ниже, чем полоса пропускания физической среды распрост­ранения. По этой причине передавать только один сигнал по линии связи невыгодно, поскольку общая полоса пропускания канала будет использо­вана незначительно. Например, полоса частот (спектр) речевого сигнала, обеспечивающая уровень разборчивости слов 90 %, составляет 3100 Гц и размещается в полосе стандартного телефонного канала связи в диапа­зоне 300…3400 Гц.

Для исключения влияния соседних каналов друг на друга из-за наложе­ния спектров, вызванных неидеальностью полосовых фильтров, в качестве расчетной ширины полосы телефонного канала принимается величина 4 кГц. При этом защитная полоса частот между двумя соседними канала­ми составляет 900 Гц.

Вместе с тем полоса пропускания кабельной линии связи (спектр эффек­тивно передаваемых частот) может составлять несколько мегагерц, что позволя­ет передавать по данной линии связи сотни и тысячи речевых сигналов. Для реализации такой многоканальной системы передачи частотные спектры различных сигналов должны быть сдвинуты относительно друг друга так, чтобы они занимали неперекрывающиеся частотные полосы. Это достига­ется применением в аналоговых системах передачи высокочастотных несу­щих синусоидальных колебаний, параметры которых (амплитуда, частота и фаза) изменяются (модулируются) пропорционально величине передавае­мых полезных сигналов.

Вопрос Системы счисления, используемые в компьютере.

Система счисления - это знаковая система, в которой числа записываются по определенным правилам, с помощью символов некоторого алфавита.

Символы алфавита, которые используют для записи чисел, называют цифрами.

Цель создания системы счисления - выработка наиболее удобного способа записи количественной информации.

Удобная система счисления должна обладать следующими свойствами:

· простота и краткость записи на материальном носителе

· однозначность представления

· удобство выполнения арифметических операций над числами

· легкость и наглядность обучения основам работы с числами

Системы счисления бывают:

1. Позиционные (десятичная)

2. Непозиционные (римская)

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.

Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.

Причины, по которой она оказалась общепринятой, совсем не математического характера. Десять пальцев рук – вот тот первоначальный аппарат для счета, которым человек пользовался с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т.е. использовав до конца возможности нашего природного «счетного аппарата», естественно принять само число 10 за новую, более крупную единицу (единицу следующего разряда).

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

Каноническим примером непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы.

Системы счисления, используемые в компьютерах:

Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.

Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7.

Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать уже шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F.

Вопрос. Двоичная арифметика

Из всех позиционных систем особенно проста двоичная система счисления. Рассмотрим выполнение основных арифметических действий над двоичными числами.

Все позиционные системы счисления "одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

• справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;
• справедливы правила сложения, вычитания и умножения столбиком;
• правила выполнения арифметических операций опираются на таблицы сложения и умножения.

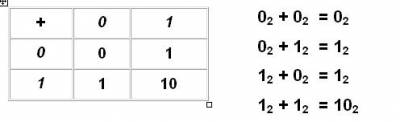
Сложение

Рассмотрим примеры на сложение.

При сложении столбиком двух цифр справа налево в двоичной системе счисления, как в любой позиционной системе, в следующий разряд может переходить только единица.

Результат сложения двух положительных чисел имеет либо столько же цифр, сколько у максимального из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица.

Вычитание

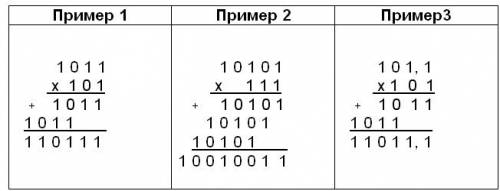
Рассмотрим примеры на вычитание.

При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак.

Умножение
Рассмотрим примеры на умножение.

Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.
Рассмотрим примеры на умножение.

При выполнении умножения в примере 2 складываются три единицы 1+1+1=11 в соответствующем разряде пишется 1, а другая единица переносится в старший разряд.
В двоичной системе счисления операция умножения сводится к сдвигам множимого и сложению промежуточных результатов.

Деление

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Рассмотрим примеры на деление
Логические основы ЭВМ. Основные понятия и операции формальной логики

Вопрос. Логические основы ЭВМ. Основные понятия и операции формальной логики

Информация, обрабатываемая в ЭВМ, представляется с помощью физических величин, которые могут принимать только два устойчивых состояния и называются «двоичные переменные». Вычислительные устройства, или, в общем случае, устройства обработки информации, представляют собою совокупность элементарных логических схем, т. е. простых схем, обрабатывающих эти величины.

Логика – это наука о формах и способах мышления. Основными формами мышления являются: · понятие, · высказывание · умозаключение. Понятие - фиксирует основные, существенные признаки объекта.

Высказывание - это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т.е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным.

Для того, чтобы можно было определить истинность или ложность высказываний, не вникая в их содержание, была придумана алгебра высказываний (алгебра логики). Алгебра логики - это раздел математической логики, значения всех эле- ментов (функций и аргументов) которой определены в двухэлементном множестве: 0 (ложь) и 1 (истина). Алгебра логики оперирует с логическими высказываниями. В этой алгебре можно производить некоторые логические операции над высказываниями, получая в результате новые составные высказывания. В алгебре логики все высказывания обозначают буквами а, b, с и т.д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры Логическая переменная - это переменная, принимающая состояние, соответствующая одному из двух элементов, например, 0 (ложь) или 1 (истина). Логические выражение - составное высказывание, которое можно выразить в виде формулы, в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции. Для записи составных высказываний в виде логических выражений на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними. Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.

2. Базовые логические операции.

2.1. Операция инверсия (отрицания). Инверсия делает истинное высказывание ложным и наоборот, ложное - истинным. На формальном языке отрицание обозначают чертой над аргументом.

2.2. Конъюнкция (логическое умножение, логическое «И»). Операция логического умножения, соответствующая функции И, выдает в качестве результата значение, называемое логическим произведением. Результат операции истинен тогда и только тогда, когда истинны все входящие в него простые высказывания. На формальном языке алгебры логики операция конъюнкции обозначается значком «&» или «^» или «*» (знаком умножения). Например, F = A & B. Аргументы могут принимать значения 1 или 0 и результат тоже только значения 1 или 0. Значение логической функции F можно определить из таблицы истинности этой функции.

2.3. Дизъюнкция (логическое сложение, логическое «ИЛИ»). Операция логического сложения, соответствующая функции ИЛИ, выдает в качестве результата значение, называемое логической суммой. Результат операции истинен тогда, когда истинно хотя бы одно из входящих в него простых высказываний. На формальном языке алгебры логики операция дизъюнкции обозначается значком «+» или «\/». Например, F = A + B. Аргументы могут принимать значения 1 или 0 и результат тоже только значения 1 или 0. Значение логической функции F можно определить из таблицы истинности этой функции.

7 вопрос. Основные логические операции. Логические законы и правила преобразований

• Логическое отрицание {инверсия).

Обозначается:?А, A, not А, не А.
Высказывание А истинно при ложном А и А ложно при истинном А.

• Логическое умножение {конъюнкция).

Обозначается А&В, A and В, А*В, А^В, АВ, А и В.
Высказывание А ^ В истинно тогда и только тогда, когда оба высказывания А и В истинны.

• Логическое сложение {дизъюнкция).

Обозначается: A v В, A or В, А + В, А или В.
Высказывание A v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Остальные операции алгебры логики выражаются через первые три опе­рации: отрицание, конъюнкцию и дизъюнкцию. Перечислим их.

• Логическое следование {импликация).

Обозначается: А > В, А => В.
Высказывание А > В ложно только тогда, когда А истинно, а В ложно.
Важно: в операции импликации посылка А не обязана быть истинной, в отличие от логического оператора в языках программирования «если А, то В».
Импликация выражается через дизъюнкцию и отрицание: А => В = A v В.

• Эквивалентность (равносильность, необходимо и достаточно).

Обозначается: А ~ В, А <=> В, А = В.
Высказывание А <=> В истинно тогда и только тогда, когда значения А и В совпадают.
Эквивалентность выражается через отрицание, дизъюнкцию и конъюнкцию: А <=> В = (А v В) ^ (B v А).

• Исключающее ИЛИ.

Обозначается A XOR В.
Высказывание A XOR В истинно, когда А и В не равны.

Порядок исполнения операций задается круглыми скобками. При отсутствии скобок порядок выполнения операций следующий: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.
Формула алгебры логики (или составное высказывание) состоит из нескольких высказываний, соединенных логическими операциями. Исходные высказывания могут быть логическими переменными или логическими константами (имеющими постоянное значение ИСТИНА или ЛОЖЬ).
Логическая функция определяется на множестве логических переменных и логических констант, принимающих значение ИСТИНА или ЛОЖЬ. Значение функции вычисляется в результате выполнения логических операций с (или над) логическими операндами. Например:

F (А, В, С) = А ^ (В v С); F(x1, х2, х3) = x1 v х2 ^ х3

Логическую функцию можно задать двумя способами: логической формулой или таблицей истинности.

Таблица истинности задает значения функции при всех возможных наборах ее переменных.

Путь к файлу.

Для того чтобы найти файл в иерархической файловой структуре необходимо указать путь к файлу. В путь к файлу входят записываемые через разделитель "\" логическое имя диска и последовательность имен вложенных друг в друга каталогов, в последнем из которых находится данный нужный файл.

Например, путь к файлам на рисунке можно записать так:

C:\basic\

C:\Музыка\Пикник\

Полное имя файла.

Путь к файлу вместе с именем файла называют полным именем файла.

Пример полного имени файлов:

C:\basic\prog123.bas

C:\Музыка\Пикник\Иероглиф.mp3

Способ

1.Нажать на белое поле правой панели открытого окна «Проводника» правой клавишей мыши и выбрать, из контекстного меню, команду – «Создать» → «Папка».

2. Далее выполняете то же, что и в первом способе.

Копирование и перемещение

• Чтобы переместить какие-либо файлы или папки, необходимо сначала их найти и выделить. После того как вы их выделите, сделайте следующее. Чтобы переместить выделенные объекты, выберите в меню окна команду Правка>Вырезать. Также можно щелкнуть правой кнопкой мыши на выделенных объектах и в открывшемся меню выбрать команду Вырезать.

• Чтобы скопировать выделенные объекты, выберите в меню окна команду Правка>Копировать. Также можно щелкнуть правой кнопкой мыши на выделенных объектах и в открывшемся меню выбрать команду Копировать
• Теперь необходимо перейти в папку, в которую нужно вставить перемещаемые или копируемые файлы/папки и выбрать команду Правка>Вставить. Также можно щелкнуть правой кнопкой мыши на свободном от значков поле окна и в открывшемся меню выбрать команду Вставить.

 

v Перемещать и копировать файлы и папки можно с помощью специальных клавиатурных комбинаций, что позволит вам сэкономить немало времени. Достаточно запомнить эти комбинации, и со временем вы будете их нажимать автоматически.

Найдите и выделите файлы или папки, предназначенные для копирования и переноса.

Чтобы переместить выделенные объекты, нажмите комбинацию клавиш <Ctrl+X>, а чтобы скопировать – комбинацию клавиш <Ctrl+C>.

Теперь перейдите в папку, в которую нужно вставить копируемые или перемещаемые файлы/папки, и нажмите комбинацию клавиш <Ctrl+V>.

Если на экране открыто сразу два окна, то перенести или скопировать файлы или папки можно с помощью метода перетаскивания. Сделать это очень просто.

Расположите окна так, чтобы содержимое обоих окон было хорошо видно.

Выделите в одном окне нужные файлы или папки (одним из описанных выше способов) и, удерживая левую кнопку мыши нажатой, перетащите файлы или папки в другое окно. При этом файлы или папки будут перемещены в другое окно.

Чтобы методом перетаскивания скопировать, а не переместить файлы или папки, одновременно с левой кнопкой мыши нужно нажимать кнопку <Ctrl>. При этом рядом с указателем мыши будет отображен значок в виде плюса, свидетельствующий о том, что происходит копирование, а не перемещение данных.

v файлы и папки можно с помощью специального механизма задач. Делается это таким образом.

1. Найдите и выделите файлы или папки для перемещения.
2. В поле Задачи для файлов и папок, расположенном в левой области окна, щелкните на ссылке Переместить файл или Переместить папку. Если выделено несколько файлов или папок, щелкните на ссылке Переместить выделенные объекты.
3. В появившемся окне Перемещение элементов выберите новое место для файла или папки, а затем щелкните на кнопке Переместить. В окне Перемещение элементов можно создать новую папку, щелкнув на кнопке Создать папку и введя имя папки.

Точно так же можно копировать файлы или папки. При этом в поле Задачи для файлов и папок нужно щелкнуть на ссылке Копировать файл, Скопировать папку или Скопировать выделенные объекты. Укажите в окне Копирование элементов то, куда выделенные объекты должны быть скопированы, после чего щелкните на кнопке Копировать.

Удаление
папки (файла)

Способ

Выделить папку (файл),нажать на клавишу
Delete и подтвердить удаление в «Корзину».

2 способ

Выделить папку (файл), выбрать пункт меню
«Файл» → «Удалить» и подтвердить удаление в «Корзину».

3 способ
Нажать на папку (файл) правой клавишей мыши, выбрать
из контекстного меню «Удалить» и подтвердить удаление
в «Корзину».

Архивное копирование файлов

Основная особенность архивного копирования файлов – это сжатие файлов с целью уменьшения занимаемого архивной копией пространства на машинном носителе информации. При таком резервировании создается один архивный файл, представляющий собой набор из одного или нескольких сжатых файлов, откуда их можно извлечь в первоначальном виде. Размер сжатого файла от двух до десяти раз меньше размера файла-оригинала. Процесс записи файлов в архивный файл называется архивированием(упаковкой), извлечение файлов из архива – разархивированием (распаковкой), а архивный файл – архивом.

Архивирование производится при помощи программ-архиваторов. Наиболее распространенные программы-архиваторы имеют приблизительно одинаковые возможности, и ни одна из них не превосходит другие по всем параметрам: одни программы работают быстрее, другие обеспечивают лучшую степень сжатия файлов. Функции, выполняемые архиватором:

· помещение файлов в архив;

· извлечение файлов из архива;

· просмотр оглавления архива;

· пересылка файлов в архив и из архива (после пересылки файлы из источника удаляются);

· архивирование каталогов;

· проверка целостности архива;

· восстановление поврежденных архивов;

· защита архивов с помощью пароля.

Архиватор WinZip обладает более широкими возможностями по интеграции с другими программными средствами. WinZip способен извлекать данные из архивов с расширениями.TAR,.Z,.GZ,.TAZ и.TGZ. Такие архивы, как правило, создаются утилитами операционных систем семействаUnix или DOS. Вы можете встретить такие архивные файлы на Internet-сайтах. Кроме того, WinZip включает в себя утилиту Uuencode, которая специальным образом кодирует файлы для передачи их по электронной почте для лучшего обеспечения их целостности.
Функциональные возможности WinRAR следующие:

· полная поддержка архивов RAR и ZIP и управление архивами других форматов;

· просмотр содержимого файлов, в том числе заархивированных;

· поддержка технологии «Drag&Drop»;

· интерфейс командной строки;

· поддержка непрерывных (Solid), многотомных и самораспаковывающихся (SFX) архивов;

· восстановление физически поврежденных архивов;

· запуск программ непосредственно из архива (например, установка новой программы не распаковывая дистрибутив);

· другие дополнительные функции, например: шифрование, добавление архивных комментариев, протоколирование ошибок и пр

15. Выполнение вычислений в таблицах в MS Word. Формулы. Функции. Вычисления в тексте.

Рассмотрим способы вычислений в таблице Word:

1. Сумма строки или столбца чисел:

§ выделить ячейку, в которой будет отображаться сумма;

§ в меню Таблица необходимо выбрать команду Формула;

§ если выделенная ячейка находится в самом низу столбца чисел, Word выводит формулу =SUM(ABOVE), а если выделенная ячейка находится с правого края строки чисел, Word предлагает формулу =SUM(LEFT).

2. Выполнение вычислений в таблице Word:

§ выделить ячейку, в которую будет помещен результат;

§ в меню Таблица необходимо выбрать команду Формула;

§ если Word предлагает формулу, которая не подходит для вычислений, то ее необходимо удалить;

§ в списке "Вставить функцию" выберите функцию. Для ссылки на ячейки введите в формулу адреса этих ячеек в скобках, например для суммирования содержимого ячеек B5 и C7 введите формулу =SUM(b5,c7).

Вычисления в тексте

При работе с текстом может потребоваться выполнить некоторое вычисление и вставить результат в текст. В этом случае следует установить курсор в ту позицию, куда должен быть помещен результат вычислений, и задать команду Таблица - Формула. В поле Формула после знака равенства ввести требуемую формулу и нажать ОК.

В составленной таблице можно подсчитать сумму значений ячеек сверху или слева. Для этого следует установить курсор в соответствующей ячейке, задать команду Формула из меню Таблица. В поле Формула после знака равенства указать SUM(ABOVE) или SUM(LEFT).

В формуле также могут быть указаны координаты ячеек, ссылки на которые могут быть использованы в качестве аргументов той или иной функции.

Координаты каждой ячейки задаются при помощи двух символов – обозначений столбца и строки. Для обозначения столбцов используются буквы латинского алфавита, для обозначения строк – цифры. Первая ячейка таблицы всегда имеет координаты А1. так, чтобы в ячейке С5 получить результат умножения значений из ячеек А2 и В3, нужно в ячейку С5 ввести формулу: =Product(A2;B3). Окне формулы также можно задать формат числа.

Результатом вставки формулы является поле, которое может быть обновлено нажатием клавиши [F9].

Наиболее часто используемые функции:
AVERAGE - Вычисляет среднее арифметическое чисел в списке, суммируя их и деля полученную сумму на количество слагаемых
MAX - Выдает наибольшее значение из списка
MIN - Выдает наименьшее значение из списка
PRODUCT - Вычисляет произведение чисел в списке
SUM - Вычисляет сумму чисел в списке

 

Существует как минимум два способа вставки формул и символов в текстовый документ.

Первый способ.

Итак, первый делом открываем вкладку Вставка. В группе Символы нажимаем на пункт Формула. Если нажать на стрелочку рядом с этим пунктом, то появится выпадающее меню, где можно выбрать одно. Откроется редактор, где можно создать какую угодно формулу. из встроенных формул.

Второй способ.

Этот способ пришел к нам из предыдущих версий MicrosoftWord, но он по-прежнему не теряет своей актуальности. Многие пользуются им до сих пор.

Открываем вкладку Вставка. В группе Текст нажимаем на кнопку Вставить объект.

В появившемся окне выбираем MicrosoftEquation 3.0.

Появится редактор формул, с виду неказистый, но по функционалу не уступающий своему старшему брату.

Возобновление слияния

Если необходимо прервать работу по слиянию, основной документ можно сохранить, а слияние возобновить позже. Приложение Microsoft Office Word сохраняет источник данных и данные поля. Если использовалась область задачСлияние, Word вернется к тому ее месту, где нужно возобновить слияние.

1. Когда все будет готово для возобновления слияния, откройте документ.

Word запросит подтверждение на открытие документа, который запустит команду SQL.

2. Поскольку этот документ подключен к источнику данных, нажмите кнопку Да. Если открывался документ, о подключении которого к источнику данных было неизвестно, то, чтобы предотвратить потенциально опасный доступ к данным, нажмите кнопку Нет.

Будет отображен текст документа вместе со всеми вставленными полями.

3. Перейдите на вкладку Рассылки и возобновите свою работу.

Выбор файла данных

1. На вкладке Рассылки в группе Начало слияния нажмите кнопку Выбрать получателей.

2. Выполните одно из следующих действий:

o Используйте контакты Outlook. Если нужно использовать список "Контакты" приложения Outlook, выберите вариант Выбрать из контактов Outlook.

Дополнительные сведения об использовании списка контактов см. в разделе Советы по работе со списком контактов Microsoft Office Outlook.

o Используйте имеющийся файл источника данных. При работе с электронной таблицей Microsoft Office Excel, базой данных Microsoft Office Access или файлом другого типа выберите вариант Использовать существующий список и найдите этот файл в диалоговом окне Выбор источника данных.

В приложении Excel можно выбрать в качестве источника данных любой лист или именованный диапазон книги, в Access — любую таблицу или запрос, определенный в базе данных.

Советы по форматированию данных на листах Excel для слияния см. в разделе Советы по форматированию данных в Office Excel.

Чтобы использовать файл данных другого типа, выберите его в диалоговом окне Выбор источника данных. Если нужного файла нет в списке, выберите соответствующий тип либо пункт Все файлы в списке Тип файлов. При слиянии можно использовать файлы данных указанных ниже типов.

§ Файлы простых программ управления базами данных, для которых установлено соответствующее средство доступа OLE DB или драйвер ODBC. Несколько таких драйверов входят в состав Microsoft Office.

§ Файл HTML, содержащий одну таблицу. Первая строка таблицы должна содержать названия столбцов, а остальные — данные.

§ Электронные адресные книги:

§ Адресная книга Microsoft Outlook.

§ Список контактов Microsoft Schedule+ 7.0.

§ Все аналогичные списки адресов, созданные с помощью систем электронной почты, поддерживающих интерфейс MAPI, таких как Microsoft Outlook.

§ Документ Microsoft Word. Документ должен содержать одну таблицу. Первая строка таблицы должна содержать заголовки, а остальные строки — записи для слияния. В качестве источника данных можно также использовать источник заголовков.

§ Любой текстовый файл, содержащий поля данных, разделенные знаками табуляции или запятыми, и записи данных, разделенные знаками абзаца.

o Создайте новый файл данных в Word. Если файл данных отсутствует, выберите команду Ввести новый список и создайте список в появившейся форме. Список сохраняется в виде фала базы данных (MDB), который можно использовать многократно. Дополнительные сведения см. в разделе Создание списка.

Если вместо приложения Microsoft Word установлен выпуск Выпуск 2007 набора Microsoft Office, можно также использовать приложение Microsoft Query для конструирования запрос и извлечения необходимых данных из внешний источник данных.

Что происходит при слиянии

При слиянии данные первой строки файла данных замещают поля в основном документе, тем самым, образуя первый составной документ. Данные второй строки файла данных замещают поля, образуя второй составной документ, и т. д.

Примеры работы с полями

Из файла данных в основной документ в качестве поля можно добавить любой заголовок столбца. Это дает определенную гибкость при составлении бланков писем, наклеек, сообщений электронной почты и других составных документов. Ниже перечислены примеры.

· Подготовка письма, уведомляющего местные предприятия о том, что они выбраны для включения в ежегодный выпуск городского путеводителя. Если файл данных содержит столбец «Компания» с названием каждого предприятия бизнеса, с которым нужно войти в контакт, вместо того, чтобы вводить имя каждой компании в отдельности, можно вставить в документ поле «Компания».

· Рассылка ежеквартальных сообщений электронной почты заказчикам, оповещающих о появившихся новых продуктах и скидках. Чтобы персонализировать эти сообщения для лучших заказчиков, в файл данных можно добавить столбец «Строка приветствия», где можно ввести такое обращение, как «Уважаемая г-жа Ильина, это новое украшение, как раз то, что Вы искали». Поместив поле «Строка приветствия» в основной документ, можно таким образом включать эти обращения в конце определенных сообщений.

· Список рассылки для подписчиков информационного бюллетеня. Если файл данных включает столбец с названием «Срок истечения», содержащий даты истечения срока каждой подписки, то поместив, поле «Срок истечения» в основной документ наклейки перед выполнением слияния, можно с помощью информации на почтовой наклейке показать каждому из подписчиков дату окончания срока действия его подписки.

Можно комбинировать поля и разделять их с помощью знаков препинания. Например, чтобы сформировать точный адрес, необходимо в основной документ вставить следующие поля:

«Имя» «Фамилия»

«Строка адреса»

«Город», «Страна» «Почтовый индекс»

Для часто встречающихся случаев, таких как блоки адреса или строки приветствия, приложение Word предоставляет сложные поля — сочетание из нескольких полей. Ниже перечислены примеры.

· Поле «Блок адреса» комбинируется из нескольких полей, включающих имя, фамилию, дом и улицу, город и почтовый индекс.

· Поле «Строка приветствия» может включать в себя одно или более полей имен, в зависимости от используемых слов приветствия.

Содержимое каждого из сложных полей можно настроить. Например, в обращении можно указать официальное имя (г-н Иванов), а в приветствии использовать "Г-ну" вместо "Уважаемый".

Применение форматирования

1. Выделите поле слияния вместе с шевронами («»), в которые оно заключено.

2. На вкладке Главная в группе Шрифт задайте параметры форматирования или нажмите кнопку запуска диалогового окна Шрифт, чтобы получить доступ к дополнительным параметрам.

ВАЖНО: Чтобы уменьшить расстояние между строками в адресе на наклейке, выделите их, нажмите на вкладке Главнаякнопку запуска диалогового окна Абзац и введите 0 в поля, определяющие величину отступа перед строкой и после нее. Если используется поле слияния "Блок адреса", выделите все