
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент корреляции рангов К. СпирменаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если • закон распределения случайной величины неизвестен или он не соответствует нормальному • имеем дело с неколичественными данными (например, ординальными величинами) • выборка мала то используется коэффициент корреляции рангов К. Спирмена
где di — разность между рангами сопряженных признаков, n — число парных членов ряда. При расстановке рангов необходимо учитывать, что равным по значению величинам присваивается ранг равный среднему арифметическому их номеров в ранжированном ряду. При полной связи ранги признаков совпадут, и разность между ними будет равна 0, соответственно коэффициент корреляции будет равен 1. Если же признаки варьируются независимо, коэффициент корреляции получится равным 0 Для проверки гипотезы о значимости коэффициента корреляции Спирменаможно воспользоваться таблицей критических значений (Приложение 6). Если вычисленный коэффициент корреляции превышает табличное значение, то связь между величинами признается статистически значимой.
Контрольное задание 12 (тесты): 1. Какая связь наблюдается между переменными, представленными на данной диаграмме рассеяния?
a) обратная, пропорциональная b) прямая, сильная c) отсутствует d) прямая, средняя e) обратная, средняя 2. В каких случаях для определения взаимосвязи между случайными величинами используется коэффициент корреляции Пирсона a) для нормально распределенных признаков b) для качественных признаков c) для ординальных признаков d) для номинальных признаков e) для независимых признаков 3. Какая связь существует между величинами, если коэффициент корреляции равен -0,110 a) связь между величинами слабая и прямая; b) связь между величинами сильная и прямая; c) связи между величинами нет; d) связь между величинами слабая и обратная; e) связь между величинами сильная и обратная. 4. Определите связь между переменными, представленными на данной диаграмме рассеяния:
a) прямая и сильная b) обратная и слабая c) нелинейная d) прямая и средняя e) обратная и средняя
ЛИНЕЙНАЯ РЕГРЕССИЯ
Вернемся к графику, который показывает зависимость между ростом и весом (рисунок 24). Мы уже оговорили, что между этими величинами существует связь и эта связь линейная. А теперь попытаемся вывести некоторую функцию (математическое правило), которая позволяла бы определять, хотя бы приблизительно, изменение веса при изменении роста. Регрессия – это функция, связывающая зависимую величину y с независимой величиной x. Она показывает, как в среднем изменяется y при изменениях x. Из математики нам известны различные функции: линейная, квадратичная, экспоненциальная, тригонометрические и т.д. Простейшей функцией является линейная, график этой функции изображен на рисунке 28. Уравнение линейной регрессии имеет вид
Основная задача регрессионного анализа найти постоянные коэффициенты b0 и b1 и оценить их статистическую значимость. Дело в том, что через точки на диаграмме рассеяния можно провести сколь угодно много прямых линий (вывести множество функций), все они будут отличаться друг от друга коэффициентами b0 и b1. Необходимо выбрать из них такую, которая наилучшим образом описывает связь между y и x. Одним из способов сделать это применить метод наименьших квадратов (МНК). Как уже отмечалось, уравнение регрессии показывает, как в среднем меняется y, т.е. конкретные его значения, полученные в опыте, и рассчитанные по уравнению могут не совпадать – есть некоторая ошибка. Из рисунка 27 видно, что для одних значений y эта ошибка меньше, для других – больше. Суть МНК в том, чтобы вывести такое уравнение регрессии, для которого сумма квадратов всех ошибок была бы наименьшей. После некоторых математических выкладок, которые мы здесь приводить не будем, можно получить, что такое уравнение имеет следующие коэффициенты b1 и b0.
Рисунок 27. Метод наименьших квадратов
Уравнение регрессии фактически является математической моделью взаимосвязи двух случайных величин. Качество этой модели, т.е. насколько хорошо она отражает эту связь, можно оценить с помощью коэффициента детерминации R2, который равен квадрату коэффициента корреляции между величинами (×100 %). Он показывает, сколько процентов исходных (выборочных) данных вписывается в полученную модель, или какой процент изменчивости y объясняется влиянием x.
Уравнение регрессии, как правило, используются для прогноза, т.е. по нему, зная величину x, можно вычислить возможное значение y. При этом вы должны быть уверены, что общая тенденция развития явления сохранится за пределами наблюдений. В противном случае прогноз можно осуществлять только в пределах наблюдаемых значений x. Предположим мы прогнозируем некоторое значение у при заданном х=х0. Тогда доверительный интервал для прогноза составляет
где – среднеквадратичное отклонение у вследствие ошибок модели, t критерий Стъюдента для заданного α и f=n2
Если независимых переменных много x1, x2, x3, x4, т.д., то возможно построение уравнение множественной линейной регрессии
Например, САД зависит от возраста, ИМТ, рациона питания и т.д. (см. Таблицу 57). Таблица 57. Результаты статобработки
Уравнение регрессии имеет вид
В данном примере коэффициент множественной корреляции равен 0,6, т.е. модель объясняет до 36% вариаций систолического артериального давления. Она является статистически значимой (т.е. не случайной). Если судить по p уровню, то САД зависит от возраста, содержания холестерина в крови и от индекса массы тела. Связь с уровнем липидов не подтверждается. В таблице 58 приведены частные коэффициенты корреляции отдельных признаков с САД, а также оценка их статистической значимости. Самая сильная связь наблюдается с индексом массы тела (r = 0,563), с возрастом и уровнем холестерина связь слабая, а с ЛПВП статистически незначимая.
Таблица 58. Частные коэффициенты корреляции
Перед использованием множественной регрессии проверьте соблюдение некоторых условий: - зависимая величина является количественной непрерывной, а независимые могут быть количественными или ординальными - независимые величины не должны сильно коррелировать между собой, в этом случае нужно отобрать один наиболее значимый признак - число наблюдений должно примерно в 10 раз превосходить число анализируемых признаков Если взаимосвязь между величинами имеет более сложный характер, чем линейный, то возможны нелинейные модели, например такого вида
Для анализа таких моделей также существуют статистические методы, однако для их освоения требуются специальные математические знания. Описание этих методов можно найти в специальной литературе.
Контрольное задание 13: По данным из таблицы 59 вывести уравнение регрессии. Для этого воспользоваться мастером диаграмм программы MS Excell. Определить концентрацию гормона в моче у лиц возраста 70 лет.
Таблица 59. Данные к заданию
АНАЛИЗ ВЫЖИВАЕМОСТИ
Анализ выживаемости статистический анализ, разработанный для изучения, оценки и сравнения времени, прошедшего до наступления некоторого события (появления метастазов, выздоровления, гибели, обострения заболевания). Выживаемость S(t) (Survive) – вероятность «прожить» время большее t с момента начала наблюдения. Термин впервые был введен страховыми агентами, которые оценивали продолжительность жизни.
Если все наблюдения начались одновременно и закончились одновременно, то
Таким образом, выживаемость– это вероятность ненаступления события до некоторого момента времени. События могут быть различные, не только нежелательные (гибель объекта), но и желательные – выздоровление, беременность при лечении от бесплодия, вступление в брак … Свойства функции S(t) S(t) =1, если t =0: в самом начале исследования ожидаемое событие не произошло ни у кого из наблюдаемых. Вероятность “дожития” до этого момента равна 1. S(t) =0, если t =∞: в конце исследования событие произошло у всех наблюдаемых. Вероятность “дожития” до этого момента = 0. График функции S(t) – кривая выживаемости отражает вероятность пережить любой из моментов времени t (рисунок 29). Время может измеряться в любых известных единицах (дни, месяцы и др).
Рисунок 29. Кривая выживаемости
График может быть крутым, тогда говорят, что выживаемость низкая, т.е. ожидаемое событие наступило быстро у всех испытуемых. График может быть пологим, тогда выживаемость – высокая, т.е. потребовалось много времени, чтобы ожидаемое событие наступило у всех испытуемых. Кривая выживаемости используется, в частности, для определения медианы выживаемости и других процентилей времени жизни. Время, до которого доживет половина испытуемых, называется медианой выживаемости (Ме). Если событие не наступило у половины испытуемых вообще, то медиану определить невозможно, тогда определяют, время, до которого “дожили” (т.е. событие не наступило) три четверти всех испытуемых (75%). При сравнении двух кривых и более, по медиане можно оценить выживаемость в разных группах. Для построения кривой выживаемости необходимо одновременно начать наблюдение за всеми привлеченными к исследованию и всех «довести» до наступления события. Как правило, не все наблюдения начинаются одновременно, и не все заканчиваются одновременно, по разным причинам. Случается, что больной покидает больницу досрочно, или само исследование заканчивается до наступления события у данного конкретного участника, и мы не знаем, что с ним произошло в дальнейшем. Т.е. мы имеем дело с неполными (цензурированными) данными. Для построения кривой выживаемости по цензурированным данным используется метод КапланаМайера. Предварительно строится так называемая таблица времени жизни.
Таблица 60. Таблица времени жизни
Выживаемость рассчитывается как произведение по всем моментам времени, когда произошло хотя бы одно событие
Вернемся к проблеме эффективности химиотерапии у больных с грибковым заболеванием кожи. Проведено исследование: I группа: 40 пациентов, получавших от 1 до 8 курсов специфической химиотерапии (преимущественно проспидином). II группа: 32 пациента, никогда не получавших цитостатики, у которых применялись различные комбинации витаминотерапии, гормонотерапии, иммуностимулирующей и лучевой терапии (рисунок 32).
Рисунок 32. Сравнение кривых выживаемости
Выживаемость пациентов с момента начала заболевания в группе II лучше, чем в группе I (рис. 32). Медиана выживаемости в группе I составила 24 года, в группе II медиана выживаемости не определяется, так как за время наблюдения за группой умерло менее половины наблюдаемых. Заключение. Результаты нашего исследования позволяют сделать вывод о том, что цитостатическая терапия отрицательно повлияла на продолжительность жизни больных лимфомами кожи низкой степени злокачественности в изученной группе. Проведенный ретроспективный анализ выживаемости выявил отчетливую закономерность во влиянии проводимой терапии на отдаленные результаты лечения и выживаемость пациентов, что может послужить достаточным базисом для выработки обоснованной тактики лечения больных изученной патологией.
Контрольное задание 14: По данным из таблицы 62 определите какова вероятность дожить до 17 часов
Таблица 62. Данные к заданию
МЕТОДЫ ПРОГНОЗИРОВАНИЯ Обычно под прогнозированием понимается процесс предсказания будущего основанное на некоторых данных из прошлого, т.е. изучается развитие интересующего явления во времени. Тогда прогнозируемая величина рассматривается как функция времени В этом разделе мы познакомимся с прогнозированием во времени. Как уже было отмечено, прогноз осуществляется на основании некоторой информации из прошлого (базы прогноза). Прежде чем подобрать метод прогнозирования полезно хотя бы качественно оценить динамику изучаемой величины в предыдущие моменты времени. На представленных графиках (рисунок 33) видно, что она может быть различной. В первом случае наблюдается относительная стабильность с небольшими колебаниями вокруг среднего значения. Во втором случае динамика носит линейно возрастающий характер, в третьем – зависимость от времени нелинейная, экспоненциальная. Четвертый случай – пример сложных колебаний, имеющих несколько составляющих.
Рисунок 33. Виды динамики
Экстраполяция – наиболее распространенный метод краткосрочного прогнозирования (13 временных периода) заключающийся в продлении предыдущих закономерностей на будущее. Применение экстраполяции в прогнозировании базируется на следующих предпосылках: • развитие исследуемого явления в целом описывается плавной кривой; • общая тенденция развития явления в прошлом и настоящем не претерпит серьезных изменений в будущем.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.163 (0.011 с.) |

 (49)
(49)


 (50)
(50) где
где  – зависимая переменная, x – независимая переменная, b0 и b1 – постоянные коэффициенты
– зависимая переменная, x – независимая переменная, b0 и b1 – постоянные коэффициенты (51)
(51) (52)
(52)
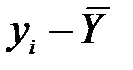
 )(
)( )
)
 )2
)2


 165
165
 79
79

 (53)
(53) (54)
(54)


 (55)
(55)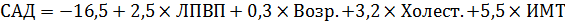
 (56)
(56) (57)
(57)

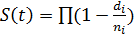 (58)
(58) Рисунок 30. График времени жизни
Пациенты Г, И достигли ремиссии на 3 и 8 месяце исследования, и по окончании исследования оставались в ремиссии и не дали рецидива. Пациент Д достиг ремиссии на 3 месяце и через 11 месяцев выписался (уехал), про него не известно, был ли рецидив. Всех их будем считать выбывшими.
Начало горизонтальной линии обозначает начало ремиссии, закрашенный кружок на конце линии – время наступления рецидива. Если нет информации о времени наступления рецидива – кружок прозрачный.
Представим данные таким образом, как будто ремиссия у всех началась одновременно в t =0 (рис. 30Б). Теперь на шкале времени не астрономические время, а время наблюдения. Такое представление данных облегчит нам дальнейшие расчеты.
Результаты расчета выживаемости занесем в сводную таблицу.
Первый рецидив наступил у пациента К через 2 месяца. Наблюдались в это время все 10 пациентов. Значит, вероятность рецидива через 2 месяца – d2/n2 =1/10=0,1. Соответственно, вероятность не наступления рецидива через 2 месяца:
Рисунок 30. График времени жизни
Пациенты Г, И достигли ремиссии на 3 и 8 месяце исследования, и по окончании исследования оставались в ремиссии и не дали рецидива. Пациент Д достиг ремиссии на 3 месяце и через 11 месяцев выписался (уехал), про него не известно, был ли рецидив. Всех их будем считать выбывшими.
Начало горизонтальной линии обозначает начало ремиссии, закрашенный кружок на конце линии – время наступления рецидива. Если нет информации о времени наступления рецидива – кружок прозрачный.
Представим данные таким образом, как будто ремиссия у всех началась одновременно в t =0 (рис. 30Б). Теперь на шкале времени не астрономические время, а время наблюдения. Такое представление данных облегчит нам дальнейшие расчеты.
Результаты расчета выживаемости занесем в сводную таблицу.
Первый рецидив наступил у пациента К через 2 месяца. Наблюдались в это время все 10 пациентов. Значит, вероятность рецидива через 2 месяца – d2/n2 =1/10=0,1. Соответственно, вероятность не наступления рецидива через 2 месяца:
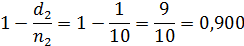 Следующий рецидив случился на 6 месяце у пациента Е. К этому времени в ремиссии были 9 пациентов. Вероятность рецидива через 6 месяцев составляет d6 /n6 = 1/9 = 0,111, а вероятность не наступления рецидива через 6 месяцев 1 0,111=0,889
Теперь мы можем оценить вероятность прожить без рецидивов более 6 месяцев, то есть S(6). Прожить без рецидивов более 6 месяцев — это значит не иметь рецидив через 2 месяца и через 6 месяцев. То есть, по правилу умножения вероятностей:
S(6) = 0,900 * 0,889 = 0,800.
Перейдем к следующему печальному событию. На 7 месяце рецидив случился сразу у 2 пациентов АиВ. К этому времени в ремиссии было 8 человек. Имеем
Следующий рецидив случился на 6 месяце у пациента Е. К этому времени в ремиссии были 9 пациентов. Вероятность рецидива через 6 месяцев составляет d6 /n6 = 1/9 = 0,111, а вероятность не наступления рецидива через 6 месяцев 1 0,111=0,889
Теперь мы можем оценить вероятность прожить без рецидивов более 6 месяцев, то есть S(6). Прожить без рецидивов более 6 месяцев — это значит не иметь рецидив через 2 месяца и через 6 месяцев. То есть, по правилу умножения вероятностей:
S(6) = 0,900 * 0,889 = 0,800.
Перейдем к следующему печальному событию. На 7 месяце рецидив случился сразу у 2 пациентов АиВ. К этому времени в ремиссии было 8 человек. Имеем
 И тогда S(7) = 0,900 * 0,889 * 0,750 = 0,600.
На 8 месяце рецидив у пациента Ж. В ремиссии к этому времени 5 человек (у 4х рецидив, 1 выбыл: 10 4 1 = 5).
И тогда S(7) = 0,900 * 0,889 * 0,750 = 0,600.
На 8 месяце рецидив у пациента Ж. В ремиссии к этому времени 5 человек (у 4х рецидив, 1 выбыл: 10 4 1 = 5).
 S(8) = 0,900 * 0,889 * 0,750 * 0,800 = 0,480.
В таблице 61 расчет выживаемости приведен полностью.
Таблица 61. Расчет выживаемости
S(8) = 0,900 * 0,889 * 0,750 * 0,800 = 0,480.
В таблице 61 расчет выживаемости приведен полностью.
Таблица 61. Расчет выживаемости



 . Однако, в медицине рассматриваются и другие виды прогноза: прогнозируется диагноз, диагностическая ценность нового теста, изменение одного фактора под действием другого и т.д.
. Однако, в медицине рассматриваются и другие виды прогноза: прогнозируется диагноз, диагностическая ценность нового теста, изменение одного фактора под действием другого и т.д.


