Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод среднего абсолютного приростаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прогнозируемый уровень изучаемой величины изменяется в соответствии со средним абсолютным приростом этой величины в прошлом. Данный метод применяется, если общая тенденция в динамике линейна (для случая, приведенного на рисунке 32Б)
Где y0 – базовый уровень экстраполяции выбирается как среднее значение нескольких последних значений исходного ряда
l – число интервалов прогнозирования
Пример. По данным из таблицы 69 рассчитать прогнозное значение на t=13,14,15 В качестве базового уровня принято усредненное значение последних значений ряда, максимально трех. Таблица 69. Результаты расчетов
Метод среднего темпа роста Прогнозируемый уровень изучаемой величины изменяется в соответствии со средним темпом роста данной величины в прошлом. Данный метод применяется, если общая тенденция в динамике характеризуется показательной или экспоненциальной кривой (рисунок 32В)
где l – число интервалов прогнозирования
Прогнозная оценка будет зависеть от того, в какую сторону от основной тенденции (тренда) отклоняется базовый уровень y0, поэтому рекомендуется рассчитывать y0 как усредненное значение нескольких последних значений ряда.
Пример. Таблица 70. Результаты расчетов
Рисунок 38. Метод среднего темпа роста |
Прогнозирование на основе математических моделей
Наиболее распространенным методом прогнозирования является нахождение аналитического выражения (уравнения) тренда. Тренд экстраполируемого явления это основная тенденцию временного ряда, в некоторой мере свободная от случайных воздействий.
Разработка прогноза заключается в определении вида экстраполирующей функции y=f(t), которая выражает зависимость изучаемой величины от времени на основе исходных наблюдаемых данных. Первым этапом является выбор оптимального вида функции, дающей наилучшее описание тренда. Наиболее часто используются следующие зависимости:
• линейная  (72)
(72)
• параболическая 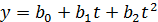 (73)
(73)
• показательная функция 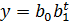 (74)
(74)
Проблемы нахождения коэффициентов линейной функции и прогноз на ее основе были рассмотрены в разделе «регрессионный анализ». Если форма кривой, описывающей тренд, имеет нелинейный характер, то задача оценки функции y=f(t) усложняется, и в этом случае необходимо привлечь к анализу специалистов по биостатистике и воспользоваться компьютерными программами по статистической обработке данных.
В большинстве реальных случаев временной ряд представляет собой сложную кривую, которую можно представить как сумму или произведение трендовой, сезонной, циклической и случайной компонент (рисунок 39).
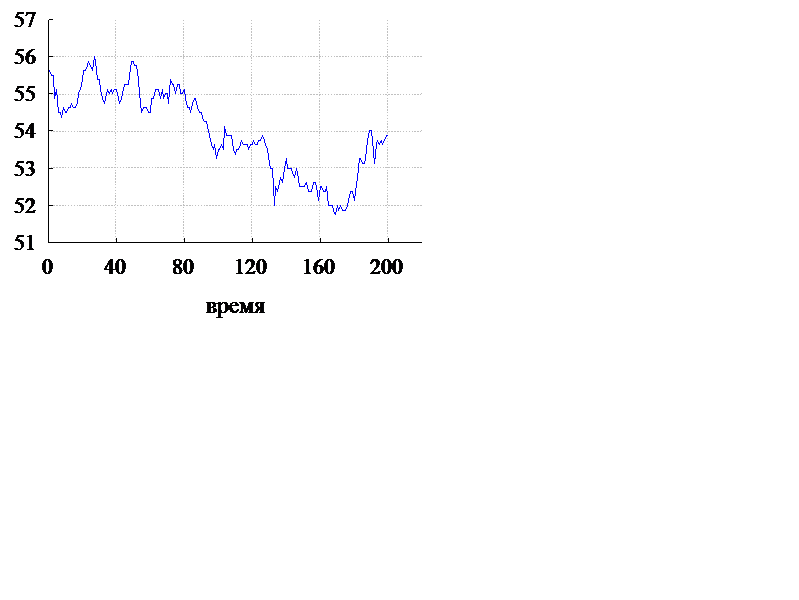
Рисунок 39. График временного ряда
Тренд представляет собой плавное изменение процесса во времени и обусловлен действием долговременных факторов. Сезонный эффект связан с наличием факторов, действующих с заранее известной периодичностью (например, времена года, лунные циклы). Циклическая компонента описывает длительные периоды относительного подъема и спада, состоит из циклов переменной длительности и амплитуды (например, некоторые эпидемии имеют длительный циклический характер). Случайная составляющая ряда отражает воздействие многочисленных факторов случайного характера и может иметь разнообразную структуру.
|
|
Анализ всех компонентов временного ряда и прогнозирование на их основе задача нетривиальная и требует специальной подготовки.
|
| Поделиться: |

 (69)
(69)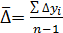 где
где 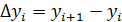
 средний абсолютный прирост уровней ряда
средний абсолютный прирост уровней ряда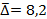

 , (70)
, (70)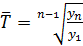 – средний темп роста в прошлом (71)
– средний темп роста в прошлом (71)