
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ качественных признаков на основе логлинейной моделиСодержание книги
Поиск на нашем сайте
Весьма распространенной проблемой в медицинских исследованиях является анализ качественных номинальных признаков, которые, как правило, представляются в виде кодов (например, цвет кожных покровов: розоватый 1, желтый 2, пунцовый 3 и т.д.). Интерес представляет частота встречаемости признаков в различных группах, а также сила и направление влияния одних признаков на другие. Нами уже были рассмотрены таблицы сопряженности 2×2, которые используются для анализа совместного распределения двух признаков, имеющих по две градации. Задачу можно сформулировать другими словами – оценка взаимного влияния двух двухуровневых факторов. Однако, встречаются более сложные случаи – многомерные таблицы сопряженности, например, нужно выяснить зависит ли срок госпитализации от возраста пациента и тяжести его состояния при поступлении в стационар (в каждую ячейку вводится число случаев
Таблица 75. Влияние двухуровневых факторов
В данном примере фактор А «срок госпитализации» имеет три уровня (i =1,2,3), фактор В «возраст» два уровня (j =1,2), и фактор С –«тяжесть состояния» три уровня (k =1,2,3). Один из способов решения подобных задач – построение логлинейной модели вида:
где λ логарифмы эффектов различных сочетаний факторов А, В, и С на различных уровнях (интерпретируется как вклад факторов и их сочетаний в частоту). Переходя от логарифмов к натуральным значениям, получают теоретические (ожидаемые) частоты Рассмотрим пример реализации логлинейного анализа в ППП STATISTICA с последующей интерпретацией результатов. Задача состоит в оценке факторов риска развития артериальной гипертензии. Анализировалась частота встречаемости следующих признаков (факторов)
Таблица 76. Факторы риска
Исходные данные представляются в виде матрицы n×m, где n количество обследованных, m число признаков. Фрагмент этой матрицы показан в таблице 77. Общий объем выборки составил 607 человек.
Таблица 77. Данные к примеру
Если какието ячейки таблицы сопряженности окажутся пустыми – не встречается данное сочетание факторов, то программа автоматически вставляет в эту ячейку величину 0,5, что никак не влияет на конечные результаты. Анализ проводится в модуле Nonlinear Estimation, для запуска которого надо в меню Statistics выбрать команду Advanced Linear/Nonlinear Models (линейные/нелинейные модели). В открывшемся меню выбрать команду Nonlinear Estimation (нелинейная оценка), а затем опцию LogLinear analysis of Frequency Tables (логлинейный анализ) – «ОК». В открывшемся окне необходимо указать форму задания исходных данных input file Raw Data, и выбрать переменные из списка, щелкнув кнопкой Variables: в нашем примере отмечаем все признаки (факторы). Нажмите ОК. В открывшемся окошке LogLinear model specification вы увидите, что фактор курения имеет код 1, потребление алкоголя 2, потребление соли 3, наследственный фактор 4, наличие гипертонии (АГ) – 5. Нажмите на кнопку Tests of Marginal and Partial Association (проверка общих и частных взаимосвязей), появятся две таблицы. Первая из них «Results of Fitting all KFactor Interactions», показывает результаты проверки нулевой гипотезы о независимости числа случаев от факторов и их сочетания. Проверка осуществляется по критерию максимального правдоподобия и по критерию хиквадрат Пирсона (таблица 78).
Таблица 78. Результаты статобработки
При К =1 и 2 р <0,05, т.е. влияние самих факторов и их попарных сочетаний статистически значимо, а сочетания по 3, 4 и 5 факторов – незначимо. Во второй таблице «Tests of Marginal and Partial Association» представлены данные о связи факторов и их сочетаний с ожидаемыми частотами наблюдений (рассчитанными по логлинейной модели) (таблица 79). Из нее видно, что статистически значимыми являются 9 эффектов (р<0,05 по критерию максимального правдоподобия и по критерию хиквадрат Пирсона).
Таблица 79. Результаты статобработки
Так как нас интересует фактор наличия артериальной гипертонии (код 5) и связь его с другими изучаемыми факторами из данной таблицы выберем статистически значимые взаимодействия – это 35 и 45. О степени влияния того или иного фактора судят по отношению
Таблица 80. Результаты статобработки
Т.е. на 49% развитие артериальной гипертензии зависит от наследственных факторов, на 4% от излишнего потребления соли и на 47% от других факторов, которые не рассматриваются в данном исследовании. Вернитесь в окошко LogLinear model specification и нажмите ОК. Появятся результаты автоматического поиска оптимальной модели для ожидаемых частот наблюдения (таблица 81).
Таблица 81. Результаты статобработки
Оптимальной оказалась модель, включающая взаимодействия 21, 53, 42, 54. Значимость модели проверяется по критериям максимального правдоподобия и по критерию хиквадрат Пирсона. Нулевая гипотеза заключается в равенстве наблюдаемых и рассчитанных по модели ожидаемых частот. Т.к. р =0,8 (т.е.>0.05) нулевая гипотеза принимается и модель считается адекватной. Более содержательный разбор наблюдавшихся частот можно провести, рассматривая таблицы 2×2 для попарного сочетания уровней факторов. Для этого нажмите кнопку Observed table (наблюдаемые частоты) и в появившемся окошке выберем, например, АГ и наследственный фактор. Появится 8 таблиц, первая из них (таблица 82)
Таблица 82. Результаты статобработки
Среди тех кто не курит, не пьет, не потребляет излишне соль гипертоники встречаются в 224/78=2,9 раза реже, чем здоровые. Причем среди гипертоников лиц с наследственным фактором в 45,5/35,5=1,3 больше, чем лиц без него. Такой же анализ можно провести относительно других факторов и их сочетания. Для задач прогнозирования используется опция Fitted table (ожидаемые частоты). Аналогично получаем таблицу 83
Таблица 83. Результаты статобработки
Если человек не курит, не потребляет алкоголь, не имеет наследственную отягощенность и не потребляет много соли, то вероятность АГ составляет 22,1/60,9*100%=36%, а его отсутствия 64%.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.29 (0.006 с.) |

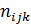 ).
).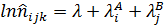 +
+ 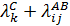 +
+ 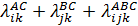 , (78)
, (78)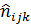 теоретические частоты наблюдений
теоретические частоты наблюдений данного фактора к сумме
данного фактора к сумме  всех факторов (в%) (таблица 80).
всех факторов (в%) (таблица 80).


