
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
СЛУЧАЙ 1. Выборки независимые.Содержание книги
Поиск на нашем сайте
В этом случае нулевая гипотеза Н(0) звучит так: • две генеральные средние равны • или - две выборки извлечены из одной генеральной совокупности • или - две совокупности имеют одинаковое распределение В медицинских задачах гипотеза может быть сформулирована, например, таким образом: содержание гемоглобина у городских и сельских жителей одинаково (подразумевая, что одинаково его распределение). Проверяемый t-критерий вычисляется по формуле
где m1, m2 - стандартные ошибки средних значений сравниваемых выборок.
Находим по таблице tкрит для заданного α и числа степеней свободы f =n1 + n2 – 2 (12)
Если │tвыч │<tкрит то принимается Н(0) (нет аргументов, чтобы ее отвергнуть)
Если │tвыч│≥tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями на соответствующем уровне значимости. Условие равенства двух генеральных дисперсий проверяется по критерию Фишера, который равен отношению большей выборочной дисперсии к меньшей:
Fкрит находится по таблице (Приложение 7) для заданного α и числа степеней свободы f1=n1-1 и f2=n2-1 (14) Если Fвыч≥ Fкрит, то гипотеза о равенстве генеральных дисперсий отвергается
Если Fвыч< Fкрит, то принимается нулевая гипотеза о равенстве.
СЛУЧАЙ 2. Выборки зависимые Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей. Такая задача возникает, когда имеются данные об изменении интересующего признака у каждого пациента. Например, если группа пациентов получала изучаемый метод лечения, и у каждого пациента измерялось значение признака до и после лечения. В данном случае предстоит проверить нулевую гипотезу о равенстве нулю изменений этого признака в результате получения терапии. При подобных исследованиях все наблюдения можно представить в виде n -пар измерений (например, до и после) Для каждой пары вычисляется разность di, где i=1, n Для полученного ряда вычисляется среднее Далее вычисляется значение критерия Стъюдента
Проверка гипотезы производится по таблицам распределения Стьюдента (Приложение 2) для выбранного уровня значимости и числа степеней свободы f= п- 1. Если │tвыч │<tкрит то принимается Н(0)
Если │tвыч│≥tкрит то принимается Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями «до» и «после».
Контрольное задание 5: 1. На каком уровне значимости можно утверждать, что содержание сахара в крови лиц основной и контрольной групп одинаково
Таблица 19. Данные к заданию
2. По данным из таблицы 20 сформулируйте нулевую и альтернативную гипотезы. Какая из гипотез будет принята. Таблица 20. Данные к заданию
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.6.140 (0.01 с.) |

 (11)
(11) – выборочные средние
– выборочные средние (13)
(13)

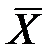 (мг%)
(мг%)
 и среднеквадратичное отклонение
и среднеквадратичное отклонение 
 (15)
(15) (уд/мин)
(уд/мин)
 (уд/мин)
(уд/мин)



