
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Байесовский подход к диагностике и прогнозированию. Последовательный анализ вальдаСодержание книги
Поиск на нашем сайте
Когда к врачу приходит пациент, врач предварительно, основываясь на интуиции и своем опыте или знаниях о распространенности болезни в популяции, имеет некоторое предположение относительно заболевания это априорная, или дотестовая вероятность. Далее, имея уже результаты клинического анамнеза и лабораторных тестов, он выстраивают картину болезни пациента, и увеличивает или уменьшает вероятность своего предположения – это апостериорная вероятность. В свете новых данных (например, по истечении некоторого времени лечения) апостериорная вероятность может быть пересмотрена. Подобный алгоритм положен в основу Байесовского классификатора. Данный подход рассчитывает вероятность того, что гипотеза истинна, путем обновления предшествующих мнений о гипотезе, по мере того как новые данные становятся доступными Метод оперирует вероятностью особого типа, известной как условная вероятность. Это вероятность события при условии, что другое событие уже произошло. Например, распространенность сахарного диабета в Европе составляет 6% (вероятность 0,06), но если у конкретного пациента обнаружено повышенное содержание глюкозы в крови, то вероятность обнаружить у него сахарный диабет резко возрастает. Апостериорная вероятность является фактически условной вероятностью гипотезы, использующей результаты исследования. Теорема Байеса утверждает, что апостериорная вероятность пропорциональна априорной, умноженной на величину, называемую правдоподобием наблюдаемых результатов (которая описывает правдоподобие наблюдаемых результатов, если гипотеза верна). Вероятность того, что событие А произойдет, если событие В уже произошло
Отношение правдоподобия положительного результата теста это шанс положительного результата теста, если пациент имеет заболевание, деленный на шанс положительного результата теста, если он заболевания не имеет. На формуле Байеса основана диагностическая процедура, которая использует метод последовательного статистического анализа А. Вальда. Рассмотрим суть этого метода. Пусть перед нами стоит задача выбора диагноза А или В. Известна распространенность этих заболеваний, т.е. априорные вероятности Р(А) и Р(В). После обнаружения у пациента признака х1
где
Тогда процесс дифференциальной диагностики выражается следующим образом
Т.е., если полученное выражение больше некоторого порогового значения А, то ставится диагноз А,если меньшенекоторого порогового значения В, то ставится диагноз В. Если ни один из порогов не достигнут, то для диагностики привлекается следующий признак х2 и проверяется неравенство
и т.д. Если использована вся имеющаяся в распоряжении информация, и ни один из порогов так и не достигнут, то делается заключение, что информации не достаточно для постановки диагноза. Пороговые значения устанавливаются по следующим формулам
где α – вероятность ошибки первого рода вероятность ложно поставить диагноз В, когда на самом деле верен диагноз А β – вероятность ошибки второго рода вероятность ошибочно поставить диагноз А, когда на самом деле верен диагноз В Вероятности ошибок первого и второго рода устанавливаются самим исследователем, исходя из сути решаемой проблемы. Для удобства вычислений используются не сами отношения шансов, а их десятичные логарифмы, умноженные на число 10, и далее округленные до целых. Полученную величину называют диагностическим коэффициентом
Пороги также выражаются через логарифмы
Тогда алгоритм диагностики имеет следующий вид
Процесс диагностики значительно ускоряется, если использовать признаки в порядке убывания их информационной ценности. Под дифференциальной информативностью признака понимается степень различия его распределения при дифференцируемых состояниях А и В. Удобной мерой для оценки информативности является мера Кульбаха
Если признак имеет диапазоны
Вопрос о минимальной информативности признака еще не нашел своего решения, но некоторые авторы рекомендуют включать в процедуру прогноза признаки с Рассмотрим пример прогнозирования послеродовых осложнений. С этой целью были сформированы две выборки: основная (п =34) это лица, у которых наблюдались послеродовые осложнения, и контрольная (без осложнений), в которую вошли 32 роженицы. Всего исследовано 20 признаков, которые имели от 2 до 3 диапазонов. Результаты всех расчетов приведены в таблице 84.
Таблица 84. Данные к примеру
В таблице 85 приведены первые 7 признаков, расположенные по мере убывания их и информационной ценности
Таблица 85. Информационная ценность признаков
Из этой таблицы видно, что наиболее значимыми признаками послеродовых осложнений являются перенесенные ОРВИ, преждевременное излитие околоплодных вод, сильное шевеление плода и т.д.
Для реализации алгоритма прогноза в данном исследовании были заданы: α – вероятность ошибки первого рода = 0,05 β – вероятность ошибки второго рода = 0,1 К вероятности α более жесткие требования, поскольку речь идет о том, что ошибочно не будут спрогнозированы послеродовые осложнения. Тогда
Т.к. по литературным данным послеродовые осложнения достигают до 26% (априорная вероятность), то
Осуществим прогноз для пациентки со следующими признаками:
Таблица 86. Алгоритм прогнозирования
Уже на четвертом шаге превышается верхний порог и прогнозируются послеродовые осложнения.
ОПРЕДЕЛЕНИЕ РАЗМЕРА ВЫБОРКИ
Методы планирования размера выборки базируются на предположении, что к окончанию наблюдения будет возможно подтвердить или опровергнуть наличие предполагаемых различий между исследуемыми группам. Шанс выявления статистически значимых различий зависит от размера выборки и величины истинного различия сравниваемых показателей. Если в исследование включено небольшое количество пациентов и при этом не выявлен эффект, то встает вопрос, с чем это связано – с недостаточностью данных, или действительным отсутствием разницы. С другой стороны, неоправданное увеличение размера выборки неэффективно с точки зрения финансовых, трудовых и организационных затрат. Для того, чтобы рассчитать оптимальный объем выборки следует определить следующие величины: 1. Мощность критерия – способность критерия обнаружить статистически значимые различия, если они действительно существуют. Планируя исследование необходимо знать мощность используемого критерия. Имеет смысл начинать исследование, когда есть хороший шанс обнаружить клинически значимые различия. И нет смысла тратить ресурсы на 40% вероятность подтверждения эффекта нового лечебного средства. Обычно мощность выбирается на уровне 7080% (β = 0,2 0,3). 2. Уровень значимости α и– задается самим исследователем. В настоящее время для клинических исследований рекомендуют выбирать альфа 0,01 или даже 0,001. 3. Вариабельность наблюдений, например, стандартное отклонение (дисперсия) для количественных признаков. Оценка дисперсии признака до начала исследования представляет собой определенную трудность. В качестве рекомендаций можно посоветовать воспользоваться ранее опубликованными данными по интересующей вас проблеме, или же самостоятельно провести небольшое пилотное исследование.
4. Наименьший клинически значимый эффект – минимальные изменения, которые мы не хотим игнорировать. Выбор его также лежит на исследователе, на его компетентности в сфере решаемой проблемы. Например, изучая реакцию на физическую нагрузку, нужно определить будет ли минимально клинически значимым изменение пульса на 5 уд/мин или же на 10 уд/мин, или же какоето иное значение.
Для сравнения количественного показателя в двух равновеликих независимых группах объем каждой выборки рассчитывается по формуле:
где Δ – минимальная (клинически значимая) величина различий, которую необходимо обнаружить
Таблица 87. Критические значения Z стандартного нормального распределения
Иногда по финансовым, этическим или другим причинам исследователь ограничен в своих возможностях набрать группу достаточной численности (как правило, это касается опытной группы). Если известна фиксированная численность одной выборки n1, то численность другой определяется следующим образом:
Если сравниваются доли p1 и p2, частота встречаемости номинального признака, то объем выборки:
здесь Δ – минимальная клинически значимая разница между долями. p1 и p2 определяется основываясь на подобных исследованиях из литературных источников, или на основе пилотного проекта. Как крайний случай можно выбрать p1 =0,5 и p2 =0,5, при этом численность выборки будет неоправданно завышена. Если доля определена в %, то в выражении вместо 1 берется 100. Такой метод дает достаточно точные результаты при 0,25<p<0,75. В других случаях вводится поправка
При этом объем выборки:
Если объем одной выборки фиксирован, то объем второй
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.55.215 (0.013 с.) |

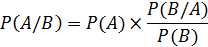 (79)
(79)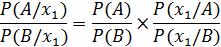 (80)
(80)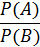 отношение априорных вероятностей
отношение априорных вероятностей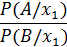 отношение апостериорных вероятностей при условии обнаружения признака х1
отношение апостериорных вероятностей при условии обнаружения признака х1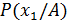 вероятность (отн. частота встречаемости) признака х1 при диагнозе А
вероятность (отн. частота встречаемости) признака х1 при диагнозе А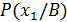 вероятность (отн. частота встречаемости) признака х1 при диагнозе В
вероятность (отн. частота встречаемости) признака х1 при диагнозе В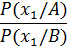 отношение правдоподобия
отношение правдоподобия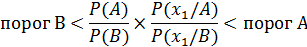 (81)
(81) (82)
(82)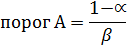 (83)
(83) (84)
(84)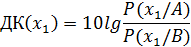 (85)
(85)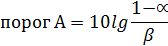 (86)
(86)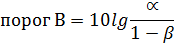 (87)
(87) (88)
(88) (89)
(89)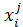 (например, возраст имеет диапазоны дети, взрослые, пожилые), то информационная ценность всего признака
(например, возраст имеет диапазоны дети, взрослые, пожилые), то информационная ценность всего признака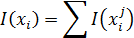 (90)
(90)

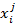

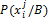
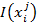

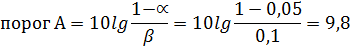
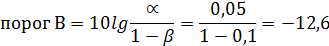
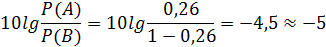
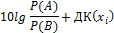
 (91)
(91) и
и  – дисперсии признака в обеих группах
– дисперсии признака в обеих группах и
и 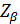 – критические значения нормального стандартного распределения для заданных α и β (односторонний или двусторонний тест, в зависимости от формулировки альтернативной гипотезы), определяются по таблицам (таблица 87).
– критические значения нормального стандартного распределения для заданных α и β (односторонний или двусторонний тест, в зависимости от формулировки альтернативной гипотезы), определяются по таблицам (таблица 87).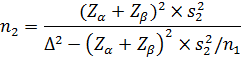 (92)
(92)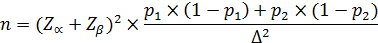 (93)
(93)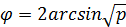 (94)
(94)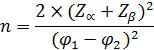 (95)
(95) (96)
(96)


