
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение трансцендентных уравнений методом секущих.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Еще одна модификация метода Ньютона связана с приближенным вычисление производной
Подставляя это выражение в формулу Ньютона (2.15), приходим к формуле
которая определяет метод секущих. Название метода связано с его геометрической интерпретацией (см. рис. 2.10). Секущая, проведенная через точки Для того, чтобы начать итерационный процесс в методе секущих необходимо задать два начальных приближения: нулевое На практике, как правило, поступают следующим образом: нулевое приближение выбирают аналогично выбору начального приближения в методе Ньютона, а в качестве первого приближения выбирают величину Затем, значения
По алгоритму метод секущих близок к методу хорд, однако в отличие от последнего начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны; кроме того при уточнении корня не проверяются знаки функции
2.4.6 Метод простых итераций Теперь рассмотрим более общий итерационный метод уточнения корней. Представим исходное уравнение
О том как преобразовать исходное уравнение к виду (2.21) буден рассказано ниже. Пусть нам известно начальное приближение к корню
Оказывается, что при определенных свойствах функции Решение трансцендентных уравнений методом простых итераций. Исходное уравнение (3.1) преобразуем к эквивалентному уравнению:
Пусть известно начальное приближение (полученное, например, на этапе отделения корней): x = x 0. Подставим его в правую часть (3.8) и получим новое приближение: x 1 = xk = В качестве условия окончания вычислительного процесса можно взять выполнение неравенства: ½ xk - xk-1 ½ < Значение x k, удовлетворяющее ему, и есть корень уравнения (3.1).Геометрическая интерпретация этого метода приведена на рис.3.8, 3.9. Здесь x * - истинное, искомое значение корня; x 0 - начальное приближение к корню; x 1, x 2, x 3 - очередные итерации. При использовании этого метода возникает вопрос о его сходимости. Дело в том, что при некоторых условиях расстояние между истинным корнем и приближениями к нему может возрастать с каждой новой итерацией, как это показано на рис.3.10, 3.11. Условием сходимости метода простых итераций является выполнение в окрестности искомого корня неравенства:
Это условие является достаточным, т.е. если оно выполняется, то процесс обязательно сходится; если же условие (3.9) не выполняется или выполняется не во всех точках x 0, x 1, x 2,..., x k,..., то заранее сказать что-либо конкретное о сходимости нельзя. Итак, для решения уравнения F (x) = 0методом простых итераций надо преобразовать его к уравнению вида x = 3.8 3.10
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.170.80 (0.006 с.) |

 в окрестности точки
в окрестности точки  по формуле
по формуле .
. ,
,  , (2.20)
, (2.20) и
и  , пересекает ось абсцисс в точке
, пересекает ось абсцисс в точке  , значение которой определяется формулой (2.20).
, значение которой определяется формулой (2.20). и первое
и первое  .
. , где e – заданная погрешность. Эти значения используются для нахождения последующего (второго) приближения
, где e – заданная погрешность. Эти значения используются для нахождения последующего (второго) приближения  по формуле (2.20).
по формуле (2.20). и
и  используют для определения третьего приближения
используют для определения третьего приближения 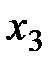 и т.д. Альтернативно, в качестве нулевого и первого приближений могут быть выбраны границы отрезка локализации корня, если они известны. В этом случае первая итерация метода секущий даст результат, аналогичный методу хорд. Для завершения итерационного процесса можно воспользоваться условием (2.14). Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной
и т.д. Альтернативно, в качестве нулевого и первого приближений могут быть выбраны границы отрезка локализации корня, если они известны. В этом случае первая итерация метода секущий даст результат, аналогичный методу хорд. Для завершения итерационного процесса можно воспользоваться условием (2.14). Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной  и поэтому оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной
и поэтому оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной  затруднено или невозможно, например, если функции
затруднено или невозможно, например, если функции  получена в ходе численных расчетов, а не задана аналитически.
получена в ходе численных расчетов, а не задана аналитически. .
. в виде
в виде . (2.21)
. (2.21) (
( ). Подставив его в правую часть уравнения (2.21) получим новое приближение
). Подставив его в правую часть уравнения (2.21) получим новое приближение  , затем аналогичным образом получим
, затем аналогичным образом получим  и так далее.
и так далее. ,
, 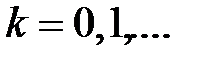 . (2.22)
. (2.22) последовательность
последовательность  , определяемая по формуле (2.22), сходится к корню уравнения
, определяемая по формуле (2.22), сходится к корню уравнения  . Необходимо установить при каких условиях итерационный процесс (2.22) будет сходящимся.
. Необходимо установить при каких условиях итерационный процесс (2.22) будет сходящимся. (x).
(x).
 .
. (x)½ < 1
(x)½ < 1
 (x)½ < 1. Сходимость к истинному корню будет тем быстрее, чем ближе к единице значение
(x)½ < 1. Сходимость к истинному корню будет тем быстрее, чем ближе к единице значение 




