
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение одношаговых методов для решения ОДУ высоких порядковСодержание книги
Поиск на нашем сайте
Преобразуем дифференциальное уравнение (7.1) n -го порядка к системе n дифференциальных уравнений 1-го порядка
Запись уравнения (7.1) в виде системы (7.16) называется формой Коши. Начальные условия (7.1') при таком преобразовании выглядят так:
Для примера преобразуем к форме Коши уравнение Бесселя:
Обозначим искомую функцию y (x) через z 1(x), а ее первую производную - z 2(x). Тогда получим систему уравнений первого порядка, эквивалентную исходному уравнению:
Вычислительный алгоритм "усовершенствованного" метода Эйлера для задачи Коши (7.16,7.16') выглядит аналогично (7.8):
где i =1,2,..., n; Вычислительный алгоритм "модифицированного" метода Эйлера для задачи Коши (7.16,7.16') выглядит аналогично (7.12):
где i =1,2,..., n; Вычислительная схема метода Рунге-Кутта четвертого порядка для задачи Коши (7.16,7.16') имеет вид:
Вопросы по 10 баллов Различие между прямыми и итерационными методами численного решения задач. Примеры. Создание мощных компьютеров существенно ослабило значение различия между методами (в таких характеристиках, как объём требуемой памяти, количество арифметических операций). В этих условия наиболее предпочтительными становятся те методы, которые не очень отличаются от лучших по скорости и удобству реализации на компьютерах, позволяют решать широкий класс задач как хорошо, так и плохо обусловленных и давать при этом оценку точности вычислительного решения. Правильность результатов может подтвердить построенный график, который в точности отображает функцию. Были исследованы два математических метода решения уравнений, к каждому из которых были представлены блок-схемы, полный текст программ и результаты машинного тестирования. Два этапа численного решения трансцендентных уравнений. В большинстве же случаев аналитическую запись корней уравнения найти очень слож-но или в принципе невозможно (такие уравнения называются трансцендентными), и поэто-му приходится решать уравнение численным способом.
Цель и сущность этапа отделения корней при решении трансцендентных уравнений. Отделение корней: На данном этапе определяются те интервалы области изменения переменной x, в каждом из которых расположен один и только один корень уравнения (3.1). По сути дела на этом этапе определяются грубые приближения значений x с погрешностью, определяемой длиной каждого найденного интервала. Полностью автоматизировать процесс отделения корней, пожалуй, невозможно, так как в нем обязательно присутствует элемент субъективного, интуитивного подхода к решению задачи. Иногда, например, интервал, в котором расположен корень, удается получить из физической сущности решаемой задачи. При выполнении этого этапа с использованием ЭВМ обычно проводится "табулирование " функции F (x, a 1, a 2,..., a k), т.е. построение таблицы ее значений при различных значениях x, следующих друг за другом с некоторым шагом h:
где x i+1 = x i + h; F i = F (x i); i = 1,2,...,n-1. Например, таблица значений функции x 2 - 12 ln½ x ½ + 6 sin x на промежутке [1,10] c шагом h = 1 имеет вид:
В качестве границ искомых интервалов выбираются такие соседние значения x, в которых соответствующие значения F (x) имеют разные знаки, так как изменение знака функции на некотором интервале означает в силу ее непрерывности, что где-то в пределах этого интервала график функции пересекает ось абсцисс, т.е. уравнение F (x) = 0 имеет корень. В частности, на основании данных из приведенной выше таблицы можно сделать вывод, что уравнение x 2 - 12 ln½ x ½ + 6 sin x = 0 на промежутке [1,10] имеет по крайней мере два корня: в интервале (2,3) и в интервале (5,6).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.25 (0.012 с.) |

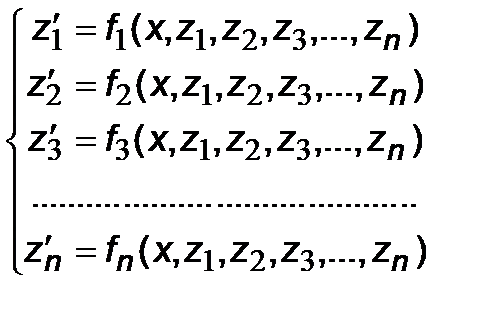
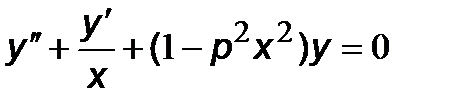 .
.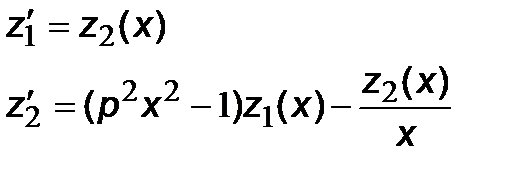
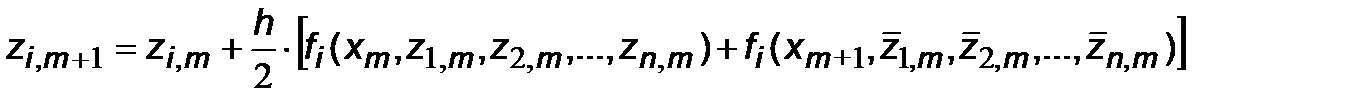
 ; k =1,2,..., n.
; k =1,2,..., n.
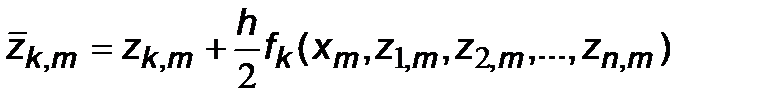 ; k =1,2,..., n.
; k =1,2,..., n.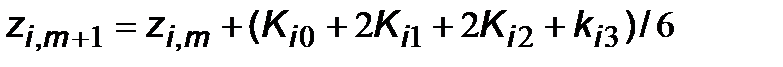 ,
,



