
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип построения аппроксимирующей функции при использовании метода наименьших квадратовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод построения аппроксимирующей функции Наиболее распространен способ выбора функции
где с 0, с 1, …, сm - коэффициенты, определяемые при минимизации величины Q. Математически минимум величины Q достигается при равенстве нулю частных производных от Q по всем коэффициентам с 0, с 1, …, сm:
Эта система линейных алгебраических уравнений относительно неизвестных с 0, с 1, …, сm называется системой нормальных уравнений, а матрица ее коэффициентов имеет следующий вид:
Элементы матрицы (5.14) являются скалярными произведениями базисных функций
Так как
Матрица (5.16) называется матрицей Грама. Расширенная матрица системы (5.13) получается добавлением справа к (5.16) столбца свободных членов
где При обработке экспериментальных данных, полученных с погрешностью Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции f (x), таких, как периодичность, экспоненциальный или логарифмический характер, симметричность, наличие асимптот и т.д. Различные варианты базисов рассматриваются достаточно подробно в [1]. Здесь рассмотрим лишь частный случай, когда аппрксимирующая функция представлена двумя базисными функциями, т.е.
Система уравнений для нахождения коэффициентов A, B выглядит так:
Решим систему (1) по правилу Крамера:
или окончательно получаем: 1.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.5.216 (0.006 с.) |

 (x) из условия минимума величины Q называется методом наименьших квадратов (далее - МНК).
(x) из условия минимума величины Q называется методом наименьших квадратов (далее - МНК). (x) = с 0
(x) = с 0  ;
;



 .
.

 , то матрицу (5.14) можно переписать в виде
, то матрицу (5.14) можно переписать в виде
 ,
,
 - скалярные произведения. аналогичные (5.15).
- скалярные произведения. аналогичные (5.15). в каждой узловой точке, обычно начинают с аппроксимации функцией
в каждой узловой точке, обычно начинают с аппроксимации функцией 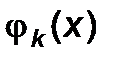 , представленной одной-двумя базисными функциями. После определения коэффициентов с k вычисляется величина Q по формуле (5.11). Если окажется, что
, представленной одной-двумя базисными функциями. После определения коэффициентов с k вычисляется величина Q по формуле (5.11). Если окажется, что  , то необходимо расширить базис добавлением новых базисных функций
, то необходимо расширить базис добавлением новых базисных функций  .
.


 ;
;
 ,
,  ;
;
 ,
,  .
.



 ,
,  .
. ,
,
 /
/
 (12)
(12) - заданные матрица и вектор и
- заданные матрица и вектор и  - искомый вектор.
- искомый вектор.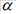 меньше единицы, т.е. для сходимости
меньше единицы, т.е. для сходимости
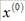 - произвольно) достаточное условие есть
- произвольно) достаточное условие есть (13)
(13)
 (14)
(14) при
при  , то
, то

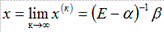 (15)
(15)



