
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный полином НьютонаСодержание книги
Поиск на нашем сайте
Ньютон предложил следующий вид интерполяционного полинома:
Коэффициенты этого полинома A 0, A 1, A 2,..., A n определяются из условий Лагранжа (5.3). Полагаем x = x 0. Тогда в (5.6) все слагаемые, кроме A 0, обращаются в нуль, следовательно, A 0 = f 0. Затем полагаем x = x 1, тогда из (5.3) имеем: f 0 + A 1(x 1- x 0)= f 1, откуда находим коэффициент A 1: A 1 = Величина f 01 = При x = x 2 полином (5.6) принимает вид: P n(x)= f 0+ f 01(x - x 0)+ A 2(x - x 0)(x - x 1), откуда с учетом (5.3) получаем: f 2 = f 0+ f 01(x 2- x 0)+ A 2(x 2- x 0)(x 2- x 1) или f 2 - f 0- f 01(x 2- x 0) = A 2(x 2- x 0)(x 2- x 1), следовательно, коэффициент A 2: A 2= где окончательно получаем выражение для A 2: A 2 = f 012 . Аналогично, при x = x 3, находим коэффициент A 3:
где Методом математической индукции можно получить для любого A k (k=0,...,n) следующее выражение:
Полученные результаты сведены в представленной ниже таблице. Следует отметить, что добавление новых узлов в исходных данных не изменяет уже вычисленные коэффициенты; таблица будет лишь дополняться новыми строками и столбцами. В интерполяционный полином Ньютона входят только диагональные элементы данной таблицы, а остальные являются промежуточными данными. Для вычисления любого элемента этой таблицы необходимы: диагональный элемент предыдущего столбца и предыдущий элемент данной строки. Поэтому в программе, реализующей данный алгоритм,
Метод наименьших квадратов Последовательность действий при аппроксимации экспоненциальной зависимостью (5.21) выглядит так: 1) вычисление логарифмов значений аппроксимируемой функции 2) вычисление коэффициентов 3) вычисление коэффициентов c и d, по формулам (5.24); 4) вычисление значений В практике обработки экспериментальных данных могут быть ситуации, когда применение лагранжевой аппроксимации (полиномиальной или сплайновой) не оправдано или в принципе невозможно. Первым примером такой ситуации могут служить случаи, когда набор экспериментальных данных был получен со значительной погрешностью, либо на измеряемую (зависимую) величину влияли некоторые дополнительные, не учитываемые факторы. Для демонстрации этой ситуации на рис.5.5 представлены экспериментальные точки, истинная неизвестная кривая f(x) и аппроксимирующая кривая В этих условиях требуется проводить аппроксимирующую кривую, которая не обязательно проходит через узловые точки, но в то же время отражает исследуемую зависимость и сглаживает возможные выбросы, возникшие из-за погрешности эксперимента.
Как и в описанных выше методах аппроксимации считаем известными значения экспериментальных данных в узлах f (x i) = f i и через
Метод построения аппроксимирующей функции Наиболее распространен способ выбора функции
где с 0, с 1, …, сm - коэффициенты, определяемые при минимизации величины Q. При обработке экспериментальных данных, полученных с погрешностью Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции f (x), таких, как периодичность, экспоненциальный или логарифмический характер, симметричность, наличие асимптот и т.д. Различные варианты базисов рассматриваются достаточно подробно в [1]. Здесь рассмотрим лишь частный случай, когда аппрксимирующая функция представлена двумя базисными функциями, т.е.
Рассмотрим частный случай линейной аппроксимации, т.е. когда график аппроксимирующей функции есть прямая линия:
где символ "надчеркивание" обозначает среднее значение:
Если требуется построить аппроксимирующую функцию, имеющую нелинейный характер относительно независимой переменной x, то иногда удается перейти к линейной зависимости. Например, пусть требуется найти аппроксимирующую функцию в виде:
Прологарифмируем значения аппроксимируемой функции f (x) в узловых точках:
и для реализации
Формулы (5.20) выглядят при этом так:
Чтобы теперь осуществить переход от функции
Величину
Методы прямоугольников Данные методы относятся к простейшим из класса методов Ньютона-Котеса. В них подынтегральная функция f(x) на каждом интервале разбиения заменяется полиномом ну-левой степени, т.е. константой. Такая замена является неоднозначной, т.к. константу можно выбрать равной значению f(x) в любой точке данного интервала разбиения.
В любом случае значение частичного интеграла определяется как произведение длины интервала разбиения на выбранную константу, т.е. как площадь прямоугольника. В зависи-мости от способа выбора аппроксимирующей константы различают методы левых, средних или правых прямоугольников (рис.6.4).
Введем следующие обозначения: точку a на оси OX обозначим через x 0, точку b - через x n, а точки разбиения промежутка [ a,b ] - через x 1, x 2,..., x n-1. Предполагается, что длина интервала разбиения постоянна на всем [ a,b ]. Обозначим ее через h:
Тогда в методе левых прямоугольников площадь каждого i -го прямоугольника
а для всего промежутка [ a,b ]: Аналогично, в методе правых прямоугольников
и в методе средних прямоугольников
где Приведенные формулы для S являются вычислительными формулами методов прямоугольников. На рис.6.5. приведена блок-схема вычисления определенного интеграла методом средних прямоугольников.
Рис.6.5. Алгоритм метода средних прямоугольников Алгоритмы для методов левых и правых прямоугольников отличаются от изображенного на рис.6.5 лишь одним блоком (он выделен жирной линией). Для метода левых прямоугольников здесь должно стоять X=A, для метода правых прямоугольников должно быть X=A+h. Оценим точность этих методов. В методе средних прямоугольников для каждого интервала разбиения получаем c учетом выражения для S i в (6.4):
Для оценки R i разложим функцию f (x) в ряд Тейлора около средней точки
В малой окрестности точки
Подставим пределы интегрирования:
или, так как
Все члены полученного при интегрировании ряда, имеющие (x - x i) в четной степени, обращаются в нуль. Поэтому получаем:
Сравнивая (6.5) и (6.7), можно записать выражение для погрешности R i:
При малой величине шага интегрирования h основной вклад в значение R i дает первое слагаемое, которое называется главным членом погрешности вычисления интеграла на интервале [ x i, x i+1] и обозначается R 0i:
Главный член полной погрешности для интеграла на всем промежутке [ a,b ] определится как сумма:
Здесь использован тот же метод средних прямоугольников, но для функции Степень шага h, которой пропорциональна величина R 0, называется порядком метода интегрирования. Как видно из (6.9 ), метод средних прямоугольников имеет второй порядок. Аналогично проведем оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора в окрестности точки x = x i:
Интегрируя это разложение почленно на интервале [ x i, x i+1] получаем
Здесь первое слагаемое есть приближенное значение интеграла, вычисленное по методу левых прямоугольников (см. формулу (6.2)), а второе слагаемое является главным членом погрешности:
Тогда на всем промежутке интегрирования [ a,b ] главный член погрешности R 0 получается суммированием частичных погрешностей R 0i:
т.е. метод левых прямоугольников имеет первый порядок. Метод правых прямоугольников также имеет первый порядок. Сравнение (6.9) и (6.11) показывает, что метод средних прямоугольников имеет меньшую погрешность по сравнению с методом левых или правых прямоугольников и за счет коэффициента в знаменателе (24 > 2), и за счет интеграла от производной, т.к. для большинства функций выполняется неравенство
Следовательно, использование метода средних прямоугольников является предпочтительным, но использовать его удается не всегда. Если значения f (x) определяются из эксперимента в дискретном наборе узлов, то метод средних прямоугольников напрямую применить нельзя из-за отсутствия значений f (x) в срединных точках. В этой ситуации приходится применять либо какие-нибудь средства интерполяции, что приводит к дополнительным расходам машинного времени и памяти, либо другие методы численного интегрирования. Метод трапеций В этом методе подынтегральная функция f (x) на интервале [ x i, x i+1] заменяется полиномом первой степени, т.е. наклонной прямой линией. Обычно эта прямая проводится через значения f (x) на границах интервала (рис.6.6). В этом случае приближенное значение частичного интеграла определяется площадью трапеции:
Блок-схему алгоритма метода трапеций предлагается студентам разработать самим. Оценим погрешность R i. Для этого разложим функцию f (x) в ряд Тейлора около точки x i:
Тогда
С помощью разложения (6.14) вычислим подынтегральную функцию в точке x i+ h:
откуда
Подставляя произведение (6.16) в выражение (6.15), получим
Сравнивая (6.12) и (6.17), получаем выражение для главного члена погрешности частичного интеграла
Тогда главный член полной погрешности метода трапеций имеет вид
т.е. метод трапеций имеет также второй порядок, но его погрешность в два раза больше, чем в методе средних прямоугольников, поэтому, если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка использовать метод средних прямоугольников.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1050; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.134.54 (0.011 с.) |

 или A 1 = f 01.
или A 1 = f 01.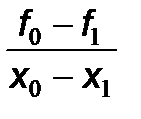 называется разделенной разностью первого порядка. При малом расстоянии между x 0 и x 1 эта величина близка к первой производной от функции f (x), вычисленной в точке x = x 0.
называется разделенной разностью первого порядка. При малом расстоянии между x 0 и x 1 эта величина близка к первой производной от функции f (x), вычисленной в точке x = x 0. =
=  =
=  =
=  ,
, . Обозначая
. Обозначая  ,
, ;
; 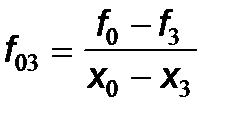 .
. .
.







 Рис.5.4. Алгоритм интерполяции
полиномом Ньютона
Рис.5.4. Алгоритм интерполяции
полиномом Ньютона
 ;
; и
и  по формулам (5.23);
по формулам (5.23); по формуле (5.21).
по формуле (5.21). (x), полученная одним из методов лагранжевой аппроксимации. Второй пример, представленный на рис.5.6, демонстрирует ситуацию, когда экспериментальные замеры в каждом узле проводились неоднократно и, вследствие погрешности измерительных приборов либо каких-либо других факторов, дали разные результаты. В этом случае применение лагранжевой аппроксимации в принципе невозможно, так как каждому узлу xi соответствует несколько разных значений fi.
(x), полученная одним из методов лагранжевой аппроксимации. Второй пример, представленный на рис.5.6, демонстрирует ситуацию, когда экспериментальные замеры в каждом узле проводились неоднократно и, вследствие погрешности измерительных приборов либо каких-либо других факторов, дали разные результаты. В этом случае применение лагранжевой аппроксимации в принципе невозможно, так как каждому узлу xi соответствует несколько разных значений fi. Рис.5.5.
Рис.5.5.
 Рис.5.6.
Рис.5.6.
 (x) обозначим непрерывную аппроксимирующую функцию. В узлах значения функций f (x) и
(x) обозначим непрерывную аппроксимирующую функцию. В узлах значения функций f (x) и  (x) будут отличаться на величину
(x) будут отличаться на величину  i = f (x i) -
i = f (x i) -  =
=  .
.
 (x) = с 0
(x) = с 0  ;
;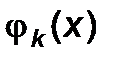 , представленной одной-двумя базисными функциями. После определения коэффициентов с k вычисляется величина Q по формуле (5.11). Если окажется, что
, представленной одной-двумя базисными функциями. После определения коэффициентов с k вычисляется величина Q по формуле (5.11). Если окажется, что  , то необходимо расширить базис добавлением новых базисных функций
, то необходимо расширить базис добавлением новых базисных функций  .
.
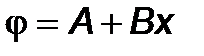 . В этом случае базисные функции имеют вид:
. В этом случае базисные функции имеют вид:  ,
,  . Тогда из (5.19) получаем:
. Тогда из (5.19) получаем: ,
,  ,
,




 .
.
 по формулам (5.20) найдем линейную аппроксимирующую функцию
по формулам (5.20) найдем линейную аппроксимирующую функцию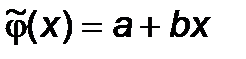
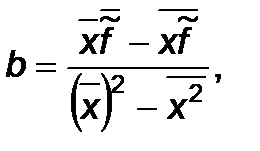
 .
.
 к функции
к функции  , надо пропотенцировать обе части равенства (5.22):
, надо пропотенцировать обе части равенства (5.22):
 обозначим
обозначим  .
.
 Левые
Левые
 Средние
Средние
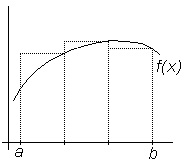 Правые
Правые
 ; x i = x i-1 + h, i =1,2,..., N.
; x i = x i-1 + h, i =1,2,..., N.
 .
.
 ), i = 0,1,2,..., n -1;
), i = 0,1,2,..., n -1;  ,
,
 , i = 0,1,2,..., n -1.
, i = 0,1,2,..., n -1.
 .
.

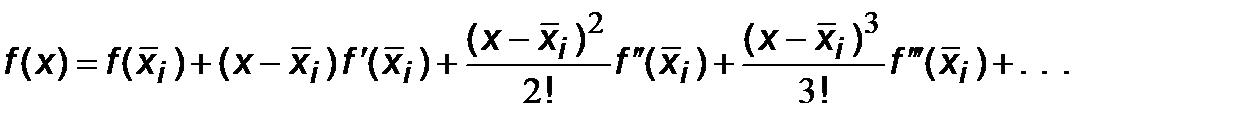
 этот ряд с высокой точностью представляет функцию f (x) при небольшом количестве членов разложения. Поэтому, подставляя под знак интеграла вместо f (x) ее тейлоровское разложение (6.6) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью. T.е. точное значение интеграла на интервале [ x i, x i+1] равно:
этот ряд с высокой точностью представляет функцию f (x) при небольшом количестве членов разложения. Поэтому, подставляя под знак интеграла вместо f (x) ее тейлоровское разложение (6.6) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью. T.е. точное значение интеграла на интервале [ x i, x i+1] равно:

 :
:
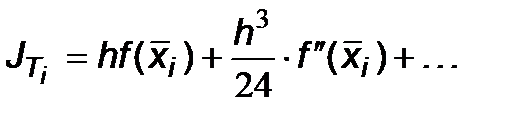

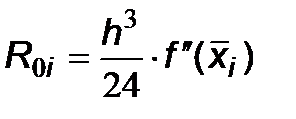 .
.
 .
.
 .
.

 .
.
 ,
,
 .
. Рис.6.6. Геометрическая
интерпретация метода
трапеций
Рис.6.6. Геометрическая
интерпретация метода
трапеций
 ,
т.е.
,
т.е. 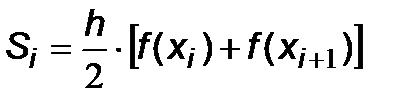 ,
а численное значение интеграла на всем [ a,b ]
,
а численное значение интеграла на всем [ a,b ]
 .
Это вычислительная формула метода трапеций.
.
Это вычислительная формула метода трапеций.



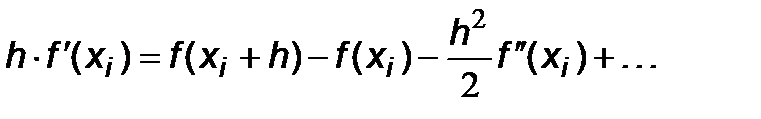

 .
. ,
,



