
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных алгебраических уравнений методом Гаусса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Блок-схема решения СЛАУ методом Гаусса
Вначале рассмотрим выполнение алгоритма метода Гаусса на примере системы 3-го порядка
Из первого уравнения (4.1’) выразим x 1:
а само это уравнение запишем в виде:
где
Подставим (4.2) с учетом (4.4) во второе и третье уравнения (4.1’) и получим систему:
где т.е. на данном этапе прямого хода из второго и третьего уравнений системы исключено неизвестное x 1. Из второго уравнения преобразованной системы (4.5) выразим x 2:
а само это уравнение запишем в виде:
где
Подставим (4.6) с учетом (4.8) в третье уравнение (4.5) и получим систему:
где т.е. на данном этапе прямого хода из третьего уравнения системы исключено x 2. Из третьего уравнения (4.9) выразим x 3: x 3 = или x 3 = Теперь система приобретает вид:
На этом заканчивается прямой ход метода Гаусса. Матрица коэффициентов полученной системы имеет вид:
Вычисление определителей методом Гаусса. При выполнении прямого хода метода Гаусса при решении СЛАУ вычисление по формулам (4.15), (4.16) производится для j=1,..., n+1, т.е. преобразованию подлежат как коэффициенты при неизвестных x 1,..., x n, так и свободные члены системы. Аналогичный алгоритм, но для j=1,...,n, может быть применен для вычисления определителя любой квадратной матрицы порядка n. Подставляя (4.15) в (4.16), получим:
где k = 1,..., n-1 - номер шага преобразования матрицы; i = k+1,...,n; j = 1,2,...,n. Так как i изменяется от k+1, то это означает, что первая строка матрицы не изменяется. Преобразование исходной матрицы по формуле (4.17) приводит к треугольной матрице, у которой элементы, расположенные ниже главной диагонали, равны нулю:
Преобразование (4.17) является линейным и поэтому не приводит к изменению определителя матрицы; но так как преобразованная матрица - треугольная, то ее определитель равен произведению элементов главной диагонали. В отличие от решения СЛАУ здесь не требуется выполнение обратного хода. Для получения максимальной точности результата надо стремиться, как и при решении СЛАУ, к тому, чтобы на каждом k-ом шаге преобразования на месте элемента а kk находился максимальный по модулю элемент из тех, что стоят в k-ом столбце ниже k-ой строки. Это достигается процедурой выбора главного элемента, поэтому при вычислении определителя надо учитывать, что перестановка любых двух строк матрицы приводит к изменению знака определителя на противоположный.
8. Обращение матриц Матрица X является обратной по отношению к заданной квадратной матрице A, если их произведение дает единичную матрицу E:
В единичной матрице элементы главной диагонали равны 1, а все остальные элементы равны 0. Как известно, произведение двух квадратных матриц A и X порядка n дает квадратную матрицу C того же порядка, элементы которой вычисляются по формуле:
Алгоритм обращения матриц, т.е. вычисления элементов матрицы X, удовлетворяющих матричному уравнению (4.18), рассмотрим на примере матриц третьего порядка:
Уравнение (4.18) с учетом формулы (4.19) для этих матриц имеет вид:
Фактически здесь записаны три СЛАУ третьего порядка:
Их особенностью является то, что все три системы имеют одну и ту же матрицу коэффициентов при неизвестных, а именно матрицу А. Итак, чтобы найти матрицу X, обратную к заданной матрице А порядка n, надо решить n систем линейных уравнений, матрицей коэффициентов которых является исходная матрица А, а вектор-столбцами свободных членов являются столбцы единичной матрицы E. При использовании метода Гаусса решения этих n систем прямой ход можно осуществить одновременно для всех систем. Расширенная матрица при этом будет иметь порядок n х 2n; ее левая половина есть матрица А, правая - матрица E.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.26.8 (0.007 с.) |


 x 2 +
x 2 +  x 3 =
x 3 =  ,
,
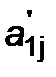 = a 1j / a 11, j = 2,3,4.
= a 1j / a 11, j = 2,3,4.
 x 2
x 2
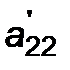 x 2
x 2
 x 3
x 3

 x 2
x 2
 x 3
x 3
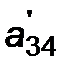
 = a ij - a i1 .
= a ij - a i1 .  ,
,
 x 3 =
x 3 =  ,
,
 =
=  /
/  x 2
x 2
 x 3
x 3

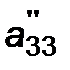 x 3
x 3

 =
=  -
-  , j = 3,4,
, j = 3,4, .
.
 ,
,










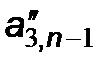





 ;
;
 ;
;




