
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородное дифференциальное уравнение 1 порядка решается при помощи подстановкиСодержание книги
Поиск на нашем сайте y= Общим решением уравнения . Частным решением уравнения
Общим решением уравнения .
Общий вид линейного дифференциального уравнения 1 порядка есть:
Линейным дифференциальным уравнением 1 порядка является уравнение: . Линейное дифференциальное уравнение решается при помощи подстановки . Общим решением уравнения
Общим решением уравнения
Общим видом уравнения Бернулли является:
Уравнением Бернулли является уравнение . Общим решением уравнения
Общим решением уравнения
Замена
Общим решением уравнения
К дифференциальному уравнению вида
Общим решением дифференциального уравнения
Замена
К дифференциальному уравнению вида
Общим решением уравнения
Общим решением уравнения
Дифференциальное уравнение
. Линейным однородным дифференциальным уравнением 2 порядка с постоянными коэффициентами называется уравнение: .
К линейному однородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:
Общим решением дифференциального уравнения
Общим решением дифференциального уравнения . Общим решением дифференциального уравнения
Общим решением дифференциального уравнения . Общим решением дифференциального уравнения
Линейным неоднородным дифференциальным уравнением 2 порядка с постоянными коэффициентами называется уравнение: . К линейному неоднородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:
Частное решение дифференциального уравнения
Частное решение дифференциального уравнения . Частное решение дифференциального уравнения
Решение дифференциального уравнения Решение дифференциального уравнения
Частное решение дифференциального уравнения .
К линейному неоднородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:
. Линейной неоднородной является система
. В уравнении колебаний струны
Уравнением свободных колебаний струны является
Решением уравнения
. Линейной системой второго порядка является
.
Линейной системой второго порядка является
.
Линейная система дифференциальных уравнений
называется однородной, если:
Однородной линейной системой первого порядка является
Неоднородной линейной системой является
Частное решение требуется найти в системе
.
Решением дифференциального уравнения
Решением дифференциального уравнения . Решением дифференциального уравнения
Решением дифференциального уравнения . Решением дифференциального уравнения
Дифференциальным уравнением с разделяющимися переменными является: . Решением дифференциального уравнения
Решением дифференциального уравнения . Решением дифференциального уравнения . Решением дифференциального уравнения . Задачу Коши требуется решить в уравнении
Задачу Коши требуется решить в уравнении
Частным решением уравнения Частным решением уравнения .
Частным решением уравнения . Частное решение следует искать в уравнении .
Однородным уравнением первого порядка является . Решением уравнения . Решением уравнения
Решением уравнения
Линейным дифференциальным уравнением является
Линейным дифференциальным уравнением является .
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |


 является:
является:
 при начальном условии y(1)=0 является:
при начальном условии y(1)=0 является: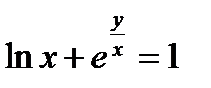
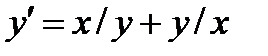 является:
является:
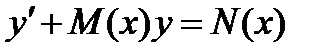


 является:
является:
 является:
является:


 является:
является: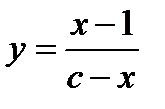
 является:
является:
 применяется в уравнении
применяется в уравнении
 является:
является:
 относится уравнение
относится уравнение
 является:
является: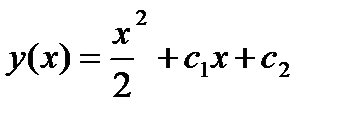
 применяется в уравнении
применяется в уравнении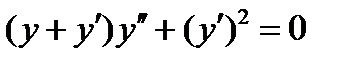
 относится уравнение
относится уравнение
 является:
является:
 является:
является:
 относится к виду
относится к виду


 является:
является:
 является:
является: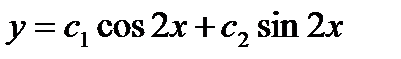
 является:
является:
 является:
является:
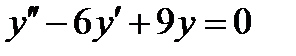 является:
является:

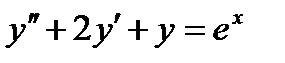
 ищется в виде:
ищется в виде:
 ищется в виде:
ищется в виде: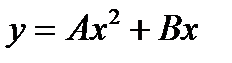
 ищется в виде:
ищется в виде: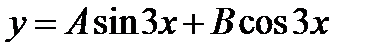
 ищется в виде
ищется в виде 
 ищется в виде
ищется в виде  , где
, где
 ищется в виде:
ищется в виде:
 Решение дифференциального уравнения
Решение дифференциального уравнения  ищется в виде
ищется в виде

 В уравнении колебаний струны
В уравнении колебаний струны  a2 равно
a2 равно
 равно
равно

 ,
, 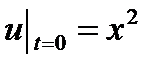 ,
,  является
является











 x(0)=2
x(0)=2 y(0)=0
y(0)=0 является:
является:
 является:
является:
 является:
является: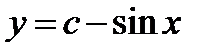
 является:
является:
 является:
является:

 является:
является:
 является:
является:
 является:
является:
 является:
является:


 при условиях у(0)=0,
при условиях у(0)=0,  является
является 
 , если y(1)=2 является
, если y(1)=2 является
 , если
, если  является
является
 ;
; 

 является
является
 является
является
 является
является





