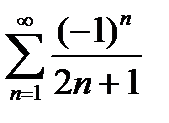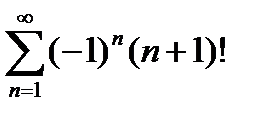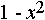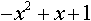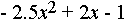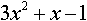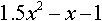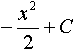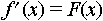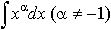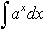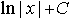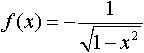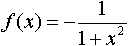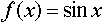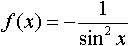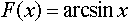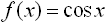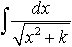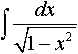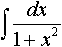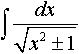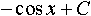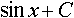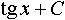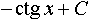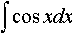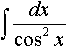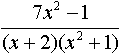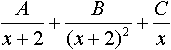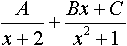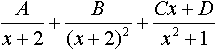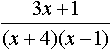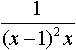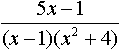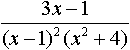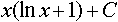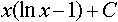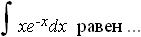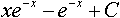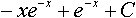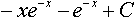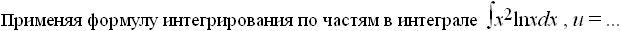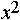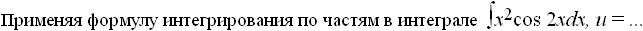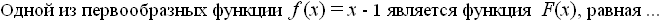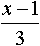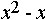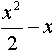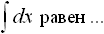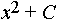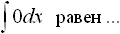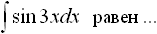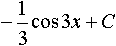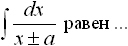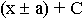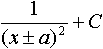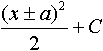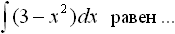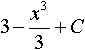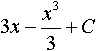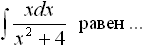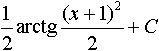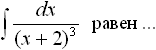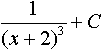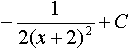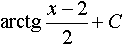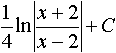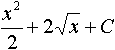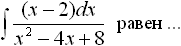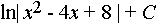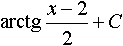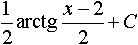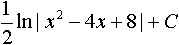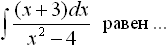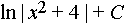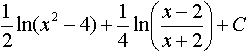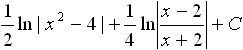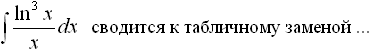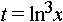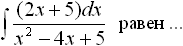Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Имеет производную в каждой точкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Не существует Условием сходимости для ряда Необходимым
S – конечное число
Ряд Сходится Ряд Расходится
Ряд D < 1 Ряд
Сходится Ряд
Расходится Исследовать ряд
Сходится Исследовать ряд Расходится Исследовать ряд
Сходится
Знакочередующийся ряд
Сходится
Ряд
Радиус R сходимости ряда
Радиус R сходимости ряда
Интервал сходимости степенного ряда
(- R; R)
R – радиус сходимости степенного ряда
[ a - R; a + R ]; (a - R; a + R). 6.3.3.3/1 Область сходимости степенного ряда (- 1; 1]
Степенной ряд для функции
называется рядом:
Тейлора
Степенной ряд для функции
называется рядом:
Маклорена
Ряд Маклорена
ex
Ряд Маклорена
sin x
Ряд Маклорена
cos x Функциональный ряд вида Фурье
Функция f (x), чётная в интервале (-
Косинусам Функция f (x), нечётная в интервале (-
Синусам Ряд
(-
i – мнимая единица. Тогда i 2 равно:
- 1
Комплексное число z = - 2 + 3 i, Re z – действительная часть z – равна:
- 2 Комплексное число z = - 2 i, Re z – действительная часть z – равна:
Комплексное число z = - 2 + 3 i, Im z – мнимая часть z – равна: 3 2
Комплексное число z = 3 + 2 i, комплексно сопряжённое число 3 - 2 i
Комплексное число z = - i, комплексно сопряжённое число i Комплексное число z = 3 + 4 i, произведение Комплексное число z = 4 + 3 i, модуль | z | комплексного числа равен: Комплексное число
Комплексное число z = 1 + i, аргумент j = arg z комплексного числа равен:
Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа
Комплексные числа z 1 = 3 + 2 i и z 2 = - 1 - i. Тогда сумма z 1 + z 2 равна: 2 + i Комплексные числа z 1 = 4 + 3 i и z 2 = - 3 + 2 i. Тогда разность z 1 - z 2 равна: 7 + i Комплексные числа z 1 = 3 + i и z 2 = 2 - i. Тогда произведение z 1 × z 2 равно: 7 - i Комплексные числа z 1 = 1 - i и z 2 = 1 + i. Тогда частное - i Комплексное число z = 1 + i. Тогда степень z 8 равна: Комплексное число
Значение функции f (z) = - z 2 - 3 i в точке z 0 = 1 - 2 i равно:
3 + i Значение функции f (z) = 2 z 2 - i в точке z 0 = 1 - 3 i равно:
- 16 - 13 i Значение функции f (z) = - 2 z 2 + i в точке z 0 = 1 + 3 i равно:
16 + 13 i Значение функции
¥
0 - ¥
Для непрерывной функции f (z) в точке z 0 выполняется:
Производной функции f (z) называется функция f¢ (z), равная:
Если функция f (z) = 5 z 2 - 7 i, то значение производной этой функции в точке z 0 = 3 - 3 i равно: 30 - 30 i Если функция f (z) = 2 z 2 - 5 i, то значение производной этой функции в точке z 0 = 5 - i равно: 20 - 4 i Если функция f (z) = 3 z 2 - 4 i, то значение производной этой функции в точке z 0 = 4 + i равно: 24 + 6 i Для того, чтобы функция f (z) = u (x, y) + iv (x, y) имела производную в точке необходимо и достаточно, чтобы в этой точке выполнялись условия:
Однозначная функция называется аналитической в некоторой области при выполнении условия:
Имеет производную в каждой точке Функция f (z) = u (x, y) + iv (x, y), тогда интеграл
Ряд
Рядом Лорана Вычетом функции f (z) относительно изолированной точки однозначного характера (ИОТОХ-а) z = a является
Вычетом функции f (z) относительно ИОТОХ-а z = a называется коэффициент cn разложения f (z) в ряд Лорана по степеням (z - a), равный c -1 Вычет функции Вычет функции
Дифференциальным уравнением второго порядка является уравнение: .(1-x2) Общим решением уравнения (1+x2)dy+ydx=0 является: . ln|y|=-arctgx+C
Дифференциальным уравнением с разделенными переменными является уравнение:
. Общим решением уравнения
Общий вид дифференциального уравнения с разделенными переменными есть: . M(x)dx+N(y)dy=0 Общим решением уравнения x2dx- . Общим решением уравнения sinxdx+e-3ydy=0 является: . 3cosx+ Общий вид дифференциального уравнения с разделяющимися переменными есть: .M1(x)N1(y)dx+M2(x)N2(y)dy=0
Дифференциальным уравнением с разделяющимися переменными является уравнение:
Общим решением уравнения 2y=2x+C Общим решением уравнения sin y sin xdy = cosycosxdx является: Csinxcosy=1 Общим решением уравнения
Решить задачу Коши требуется в уравнении: . Частным решением уравнения
Частным решением уравнения
Частным решением уравнения y= Частным решением уравнения . 2y2-4x2=1 Однородным дифференциальным уравнением 1 порядка является уравнение: . I
Значение y(x) при x=2, где y(x) - решение задачи Коши Если y(x) решение задачи Коши
Если y(x) решение задачи Коши
Значение y(x), при x=2, где y(x) - -решение задачи Коши Значение y(x), при x=1, где y(x) - решение задачи Коши
Если y(x) решение задачи Коши
e Значение y(x) при x=2, где y(x) - решение задачи Коши (1+x)dy+ydx=0,y(0)=1,) равно...
1/3 Значение y(x) при x=2, где y(x) - решение задачи Коши
Общее решение дифференциального уравнения
Общее решение дифференциального уравнения
Общее решение уравнения
Если 16+40i Если f(z)=4z2-10i, тогда значение производной этой функции в точке z0=1-3i равно... I Если f(z)=3z2-9i, тогда значение производной этой функции в точке z0=5+7i равно... 30+42i Если f(z)=5z2-7i, тогда значение производной этой функции в точке z0=3-3i равно... I Установите соответствие между знакопеременными рядами и видами сходимости.
абсолютно сходится условно сходится расходится
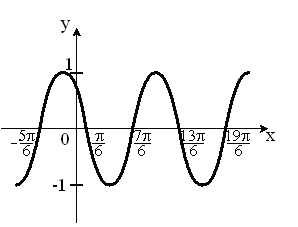
Если f(z) =6z2–i,тогда значение производной этой функции в точке z0 = l + 2i равно... 12+24i Если f(z)=2z2+15i, тогда значение производной этой функции в точке z0=1-4i равно... I Укажите вид графика периодической функции...
Если f(z)=4z2-9i, тогда значение производной этой функции в точке z0=1-i равно... I Если f(z)=4z2-i, тогда значение производной этой функции в точке z0=1+5i равно... 8+40i
Дисциплина: "Математический анализ" Дидактическая единица: "ДЕ_01_Дифференциальное и интегральное исчисление. Неопределенный интеграл_(у;пэб;;)" Уровень: 1 Код: 489899/138418 (копия/оригинал)
Уровень: 2 Код: 489905/138428 (копия/оригинал)
Уровень: 2 Код: 489901/138422 (копия/оригинал)
Уровень: 2 Код: 489904/138427 (копия/оригинал)
Уровень: 2 Код: 489903/138426 (копия/оригинал)
Уровень: 1 Код: 489896/138415 (копия/оригинал)
Уровень: 1 Код: 489900/138419 (копия/оригинал)
Уровень: 1 Код: 489902/138425 (копия/оригинал)
Уровень: 2 Код: 489917/138441 (копия/оригинал)
Уровень: 2 Код: 489977/138421 (копия/оригинал)
Уровень: 2 Код: 489976/138420 (копия/оригинал)
Уровень: 2 Код: 489970/138456 (копия/оригинал)
Уровень: 2 Код: 489918/138443 (копия/оригинал)
Уровень: 2 Код: 489969/138442 (копия/оригинал)
Уровень: 2 Код: 489948/138479 (копия/оригинал)
Уровень: 4 Код: 489947/138478 (копия/оригинал)
Уровень: 4 Код: 489932/138461 (копия/оригинал)
Уровень: 4 Код: 489931/138460 (копия/оригинал)
Уровень: 1 Код: 489930/138457 (копия/оригинал)
Уровень: 2 Код: 489972/302387 (копия/оригинал)
Уровень: 2 Код: 489971/302353 (копия/оригинал)
Уровень: 2 Код: 489907/138430 (копия/оригинал)
Уровень: 1 Код: 489916/138440 (копия/оригинал)
Уровень: 1 Код: 489915/138439 (копия/оригинал)
Уровень: 2 Код: 489956/138487 (копия/оригинал)
Уровень: 2 Код: 489933/138462 (копия/оригинал)
Уровень: 2 Код: 489922/138447 (копия/оригинал)
Уровень: 2 Код: 489937/138466 (копия/оригинал)
Уровень: 4 Код: 489929/138454 (копия/оригинал)
Уровень: 2 Код: 489926/138451 (копия/оригинал)
Уровень: 4 Код: 489935/138464 (копия/оригинал)
Уровень: 4 Код: 489934/138463 (копия/оригинал)
Уровень: 4 Код: 489936/138465 (копия/оригинал)
Уровень: 3 Код: 489923/138448 (копия/оригинал)
Уровень: 3 Код: 489942/138472 (копия/оригинал)
Уровень: 4 Код: 489973/138476 (копия/оригинал)
Уровень: 2 Код: 489928/138453 (копия/оригинал)
Уровень: 4 Код: 489945/138475 (копия/оригинал)
Уровень: 2 Код: 489909/138432 (копия/оригинал)
Уровень: 2 Код: 489955/138486 (копия/оригинал) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 условие
условие 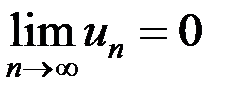 является:
является: – последовательность частичных сумм ряда
– последовательность частичных сумм ряда 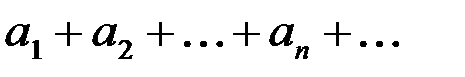 . Тогда ряд сходится, если предел
. Тогда ряд сходится, если предел 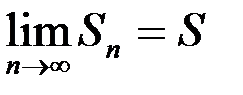 равен:
равен: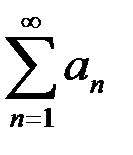 сходятся, а члены ряда
сходятся, а члены ряда 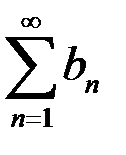 , bn £ an. Тогда ряд
, bn £ an. Тогда ряд 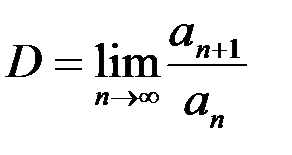 :
: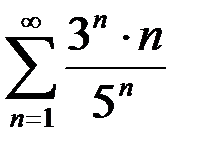 :
: :
: на сходимость по интегральному признаку:
на сходимость по интегральному признаку: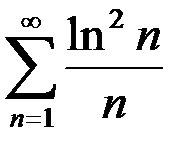 на сходимость по интегральному признаку:
на сходимость по интегральному признаку: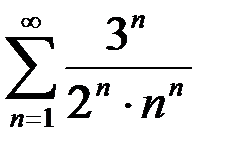 на сходимость по радикальному признаку Коши:
на сходимость по радикальному признаку Коши: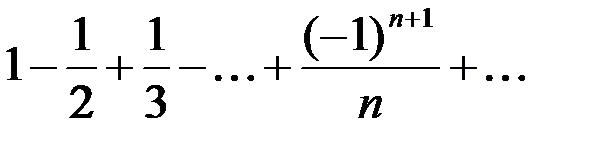 :
: сходится абсолютно, если сходится ряд:
сходится абсолютно, если сходится ряд: ;
;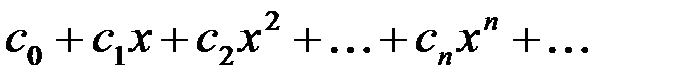 определяется по формуле:
определяется по формуле: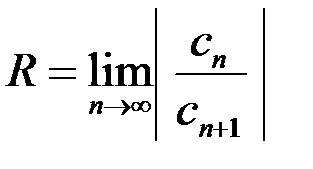 ;
; определяется по формуле:
определяется по формуле: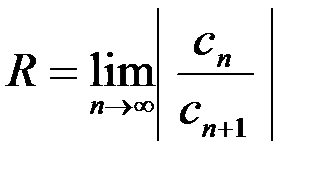 .
.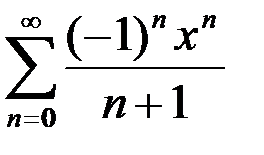 :
: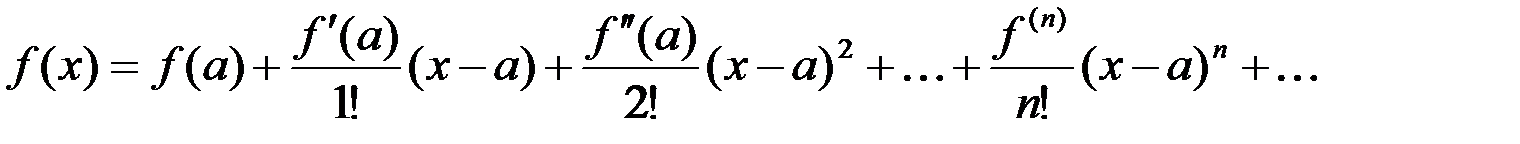
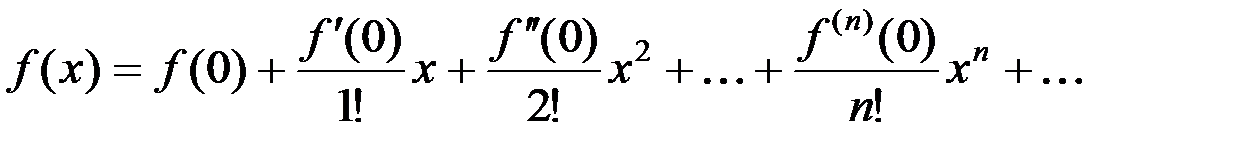
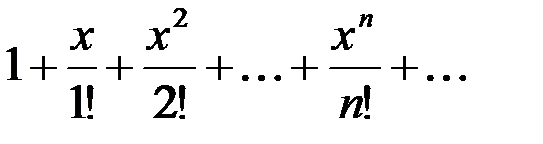 является разложением в ярд функции:
является разложением в ярд функции: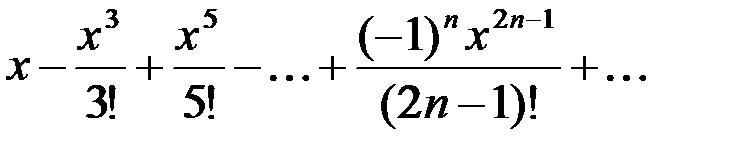 является разложением в ярд функции:
является разложением в ярд функции: является разложением в ярд функции:
является разложением в ярд функции: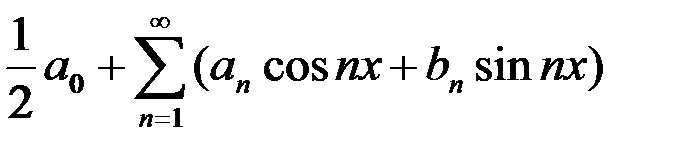 в интервале (- p; p) называется рядом:
в интервале (- p; p) называется рядом: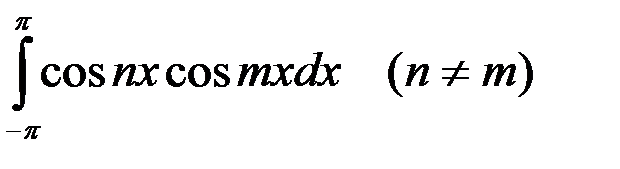 равен:
равен: равен:
равен: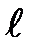 ;
; 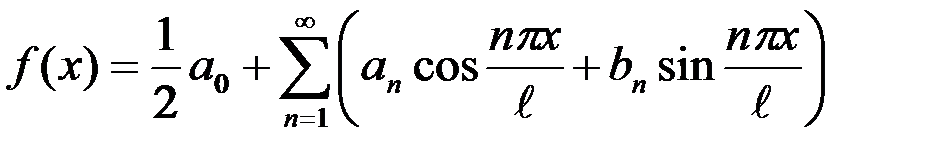 является рядом Фурье для функции f (x) в интервале:
является рядом Фурье для функции f (x) в интервале: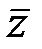 равно:
равно: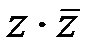 равно:
равно: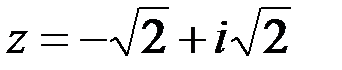 , модуль | z | комплексного числа равен:
, модуль | z | комплексного числа равен:
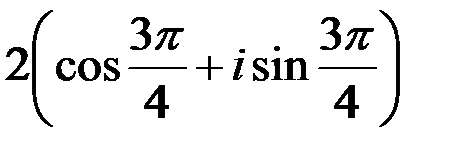 ;
; :
: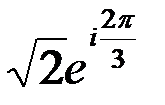
 равно:
равно: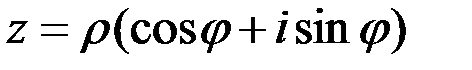 . Тогда
. Тогда 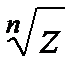 равен:
равен: ;
;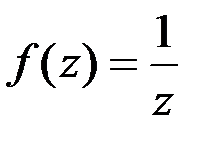 в точке z 0 = 2 i равно:
в точке z 0 = 2 i равно: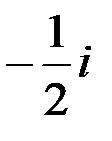
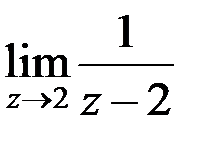 равен:
равен: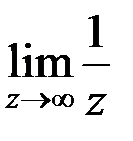 равен:
равен:
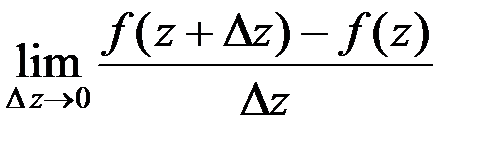
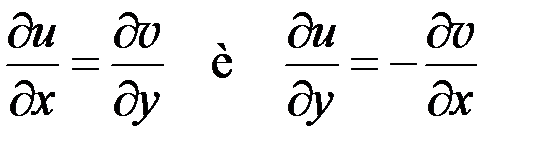
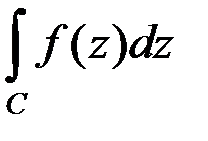 равен:
равен: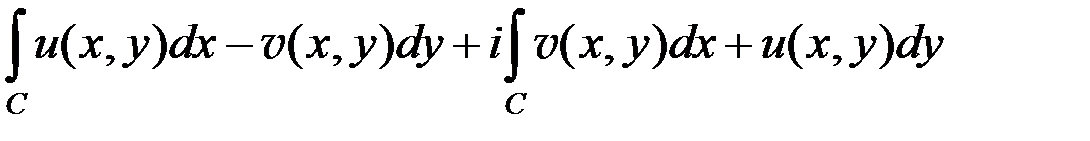
 называется:
называется: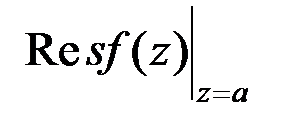 , равный:
, равный: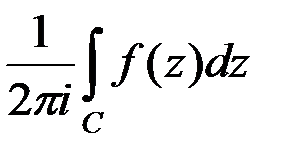
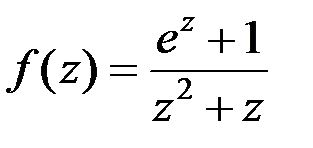 относительно точки z = 0 равен:
относительно точки z = 0 равен: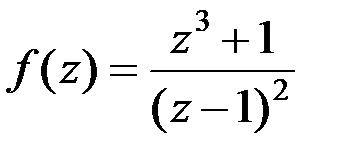 относительно точки z = 1 равен:
относительно точки z = 1 равен: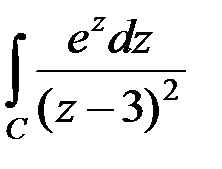 , где C: | z | = 2 равен:
, где C: | z | = 2 равен: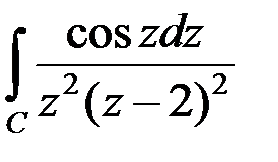 , где C: | z | = 1 равен:
, где C: | z | = 1 равен: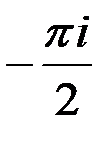
 -x
-x 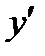 =2
=2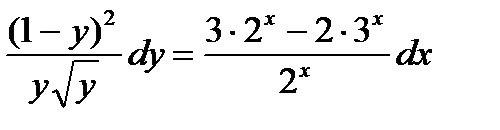
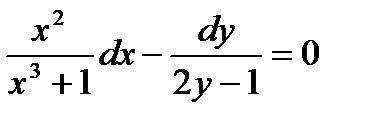 является:
является:
 =0 является:
=0 является: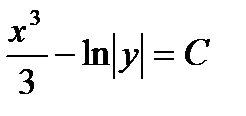

 (y+1)sinx
(y+1)sinx =2x-y является:
=2x-y является: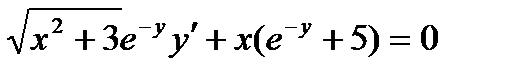 является:
является:

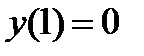
 при начальном условии у(1)=0 является:
при начальном условии у(1)=0 является: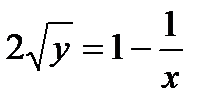
 при начальном условии у(1)=0 является
при начальном условии у(1)=0 является
 при начальном условии у(1)=0,5 является:
при начальном условии у(1)=0,5 является: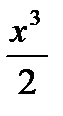
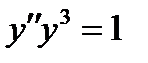 при начальных условиях у(
при начальных условиях у(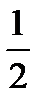 )=
)=  является:
является:
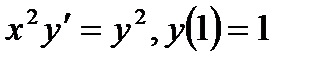 , равно...
, равно...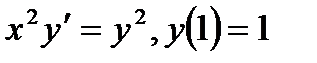 , то y(2) равно...
, то y(2) равно...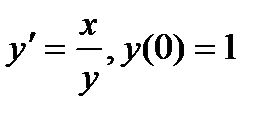 , то y(1) равно...
, то y(1) равно...
 равно...
равно... равно...
равно...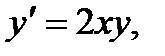 y(0)=1, то y(1)...
y(0)=1, то y(1)...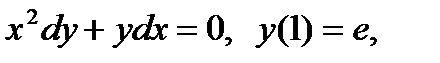 равно...
равно...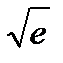
 , имеет вид...
, имеет вид...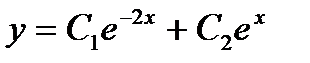
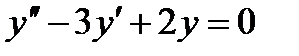 , имеет вид...
, имеет вид...
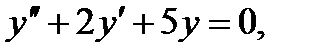 имеет вид...
имеет вид...
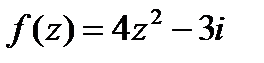 , тогда значение производной этой функции в точке
, тогда значение производной этой функции в точке 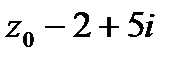 равно...
равно...