
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции в точке и на интервале. Свойства непрерывных функций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ответ: Непрерывность функции в точке. Пусть функция f (x) определена в некоторой окрестности O (x 0) точки x 0 (включая саму точку x 0). Функция f (x) называется непрерывной в точке x 0, если существует
Lim f (x), равный значению функции f (x) в этой точке:
Замечание. Равенство (1) можно записать в виде:
т.е. под знаком непрерывной функции можно переходить к пределу. Пусть Δ x = x − x 0 — приращение аргумента, Δ y = f (x) − f (x 0) — соответствующее приращение функции. Необходимое и достаточное условие непрерывности функции в точке Функция y = f (x) непрерывна в точке х0 тогда и только тогда, когда
Непрерывность функции на интервале. Определение: Пусть f - некоторая функция, D(f)- ее область определения и Свойства непрерывных функций Теорема 1. Сумма непрерывных функций есть функция непрерывная. Доказательство. Пусть функции
Согласно свойству пределов функций существование пределов функций
что и требовалось доказать. Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная. Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция. Теорема 2. Произведение непрерывных функций есть функция непрерывная. Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль. Теорема 4. Любая элементарная функция непрерывна в области своего определения. Для доказательства этой теоремы нужно показать, что для любого числа a из области определения элементарной функции
Продемонстрируем справедливость теоремы на некоторых конкретных примерах.
Первый член в правой части этого равенства представляет собой бесконечно малую функцию при x → a и, следовательно,
Теорема 5. Пусть функция Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами,
Первый замечательный предел. 1 замечательный предел. Возьмем круг радиуса 1, обозначим радианную меру угла MOB через Х. Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда Разделим все на Т.к. Понятие предела функции на бесконечности. Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство | f(x) – b | < e. Запись этого факта:
Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство | f(x) – b | < e. Записывается это так:
Второй замечательный предел Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами: Если x→∞, то n→∞, тогда По признаку о существовании пределов:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.94 (0.01 с.) |

 - некоторый (открытый) интервал (может быть
- некоторый (открытый) интервал (может быть  или
или  ) Назовём функцию
) Назовём функцию  непрерывной на интервале
непрерывной на интервале  , если
, если  , то есть для любого
, то есть для любого  (в сокращённой записи:
(в сокращённой записи: 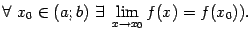
 и
и  непрерывны в точке a. Тогда
непрерывны в точке a. Тогда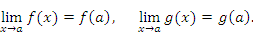


 , где n – целое положительное число. Тогда
, где n – целое положительное число. Тогда
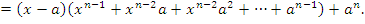
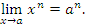
 является непрерывной в каждой точке a. Действительно,
является непрерывной в каждой точке a. Действительно,


 .
.
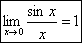

 и получим:
и получим:
 , то по признаку существования пределов следует
, то по признаку существования пределов следует  .
.








