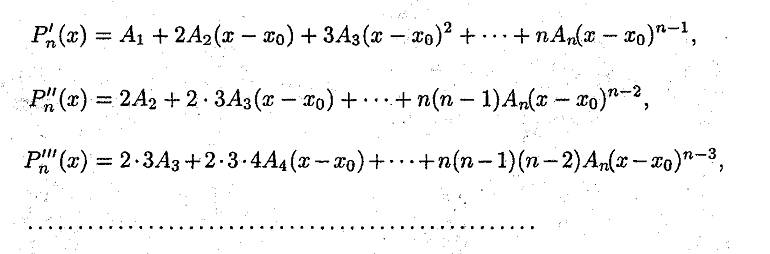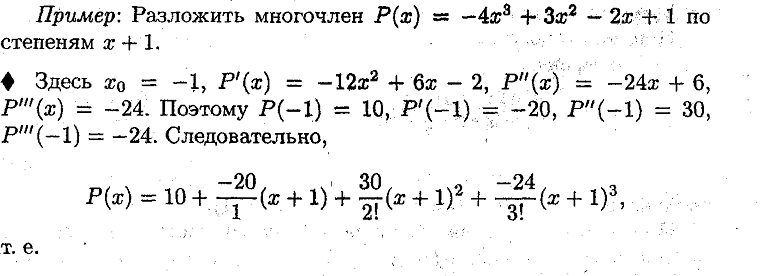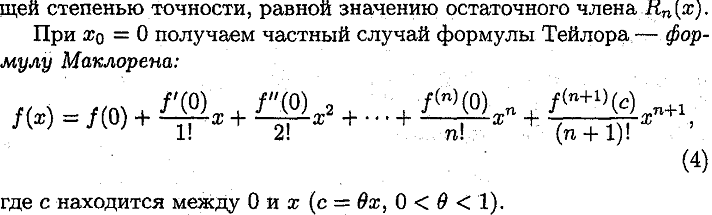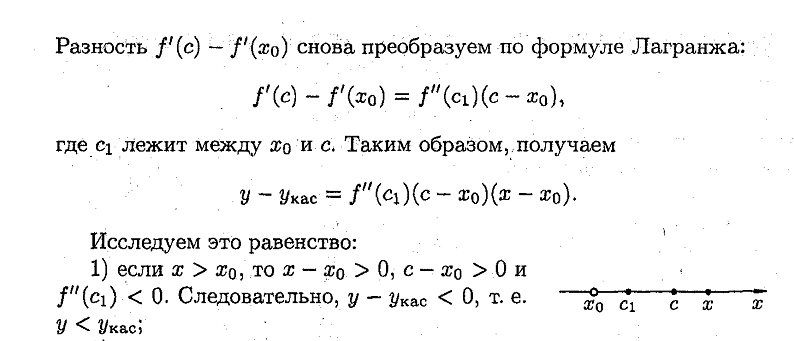Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 3. Дифференциальное исчисление.Содержание книги Поиск на нашем сайте
Раздел 3. Дифференциальное исчисление. 1. Понятие функции. Способы задания. Графики функции в декартовой системе координат. Ответ: Определение функции
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменная
Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций. Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции. Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. 3.Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений. 4.Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. Циклоида. Цикло́ида — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса, катящейся без скольжения по прямой
Вывод параметрического уравнения циклоиды. Параметрическое уравнение окружности: x = R sin(t) y = R cos(t) параметрическое уравнение прямой (горизонтальной): x = k*t y = const причем в нашем случае, y = R, тк центр окружности должен быть поднят на R над осью Ox а k должен быть равен периметру окружности (2*Pi*R) при прохождении окружностью полного цикла (2*Pi). делим одно на другое и получаем k = R. то есть уравнение прямой получилось: x = R*t y = R теперь с окружностью, В нашем случае она должна крутиться по часовой стрелке, а не против, то есть: x = -R sin(t) y = -R cos(t) Складываем эти согласованные уравнения и получаем x = R*t- R sin(t) y = R - R cos(t) Параметрическое уравнение циклоиды Понятие приращения функции, монотонность функции. Понятие функции ограниченной, четной, нечетной, периодической. Ответ: Одним словом определяет области возрастания и убывания функции Ограниченная функция. Пусть задана функция y=f(x), определенная на некотором множестве D значений аргумента. Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D. Понятие сложной функции. Понятие обратной функции. Ответ: Понятие о сложной функции Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у). Понятие обратной функции. Функция, принимающая каждое свое значение в единственной точке области определения, называется обратимой. Таким образом, функция f(x) = kx + b обратима, а функция f(x) = x2 не является обратимой. Если между величинами х и у существует функциональная зависимость, то, вообще говоря, безразлично, какую из этих величин считать аргументом, а какую – функцией. Пусть задана функция y = f(x), где y является зависимой переменной, x – аргументом. Очевидно, в этом случае x и y можно поменять ролями, т. е. x будет функцией, а y – аргументом. Тогда рассматриваемая функциональная зависимость между x и y запишется так: x = Y(y). Функция x = Y(y) называется обратной по отношению к функции y = f(x). Чтобы найти обратную функцию, нужно решить уравнение Теоремы о пределах. Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x).
Теорема 3. Предел постоянной равен самой постоянной
Доказательство. f(x)=с, докажем, что Возьмем произвольное e>0. В качестве d можно взять любое положительное число. Тогда при
Теорема 4. Функция не может иметь двух различных пределов в одной точке. Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при, то и произведение имеет предел при Теорема 7. Если функции f(x) и g(x) имеют предел при Х стремящийся к А, то и их частное имеет предел при Х стремящийся А, причем предел частного равен частному пределов. Второй замечательный предел Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами: Если x→∞, то n→∞, тогда По признаку о существовании пределов: Доказательство Необходимость. Предположим: функция дифференцируема в точке x 0, т.е. Δ y = A ·Δ x +α(Δ x)·Δ x. Разделив обе части данного равенства на Δ x, получим: Δ x Δ y = A +α(Δ x). Из определения производной функции в точке: y /(x 0)=limΔ x →0Δ x Δ y =limΔ x →0(A +α(Δ x))= A. Т.е. получили, что существует конечная производная функции в точке x 0 и y /(x 0)= A. Достаточность. Пусть существует конечная производная y /(x 0)∈ R. Покажем дифференцируемость функции. y /(x 0)=limΔ x →0Δ x Δ y.
Сложная функция.
Обратная функция.
Примеры:
ых Частного функций. Ответ:
Доказательство Пусть Следовательно
2. Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример:
Геометрический смысл.
23. Многочлены Маклорена, Тейлора порядка N для функции имеющей производные N+1 порядка в данной точке. Примеры. Ответ:
Точки перегиба. Ответ:
Раздел 3. Дифференциальное исчисление. 1. Понятие функции. Способы задания. Графики функции в декартовой системе координат. Ответ: Определение функции
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменная
Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций. Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции. Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. 3.Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений. 4.Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |


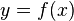 относительно Х. Если оно имеет более чем один корень, то функции обратной к
относительно Х. Если оно имеет более чем один корень, то функции обратной к  не существует.
не существует.



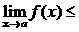
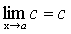
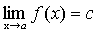

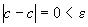
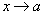 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 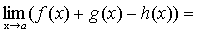
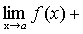
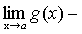
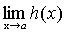














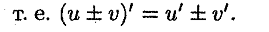





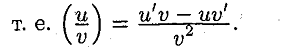
 - точка минимума. Тогда при
- точка минимума. Тогда при 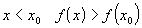 . Значение выражения
. Значение выражения  . Значит,
. Значит, 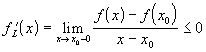 . Рассмотрим теперь
. Рассмотрим теперь  , при этом также
, при этом также  , и выражение
, и выражение  . Значит, правая производная
. Значит, правая производная  .
. . Теорема доказана.
. Теорема доказана.
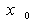 ,
,  - точка минимума, но
- точка минимума, но 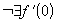 .
. , но точка 0 - не экстремум.
, но точка 0 - не экстремум.