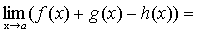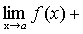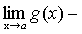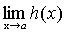Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие четной и нечетной функции.Содержание книги Поиск на нашем сайте Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
Периодическая функция- функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (пери́ода функции). Говоря более формально, функция периодична, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство Все тригонометрические функции являются периодическими.
Понятие сложной функции. Понятие обратной функции. Ответ: Понятие о сложной функции Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у). Понятие обратной функции. Функция, принимающая каждое свое значение в единственной точке области определения, называется обратимой. Таким образом, функция f(x) = kx + b обратима, а функция f(x) = x2 не является обратимой. Если между величинами х и у существует функциональная зависимость, то, вообще говоря, безразлично, какую из этих величин считать аргументом, а какую – функцией. Пусть задана функция y = f(x), где y является зависимой переменной, x – аргументом. Очевидно, в этом случае x и y можно поменять ролями, т. е. x будет функцией, а y – аргументом. Тогда рассматриваемая функциональная зависимость между x и y запишется так: x = Y(y). Функция x = Y(y) называется обратной по отношению к функции y = f(x). Чтобы найти обратную функцию, нужно решить уравнение Основные элементарные функции и их графики. (представить конспект) «Каждый из вас перепишете в тетради элементарные функции и изобразите их график. Может попадется на экзамене чтоб показали тетрадь.» 6. Понятие бесконечно малых функций, свойства бесконечно малых функций. Ответ: Функция f(x) называется бесконечно малой величиной при х, стремящемся к х0, если для любого числа, даже сколь угодно малого положительного числа
Свойства: 1.Сумма конечного числа бесконечно малых — есть величина бесконечно малая. 2.Произведение бесконечно малой последовательности на ограниченную функцию — есть величина бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая. 3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая. Понятие предела функции. Основные теоремы о пределах. Ответ: Число А называется пределом функции f(x) при Теоремы о пределах. Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x).
Теорема 3. Предел постоянной равен самой постоянной
Доказательство. f(x)=с, докажем, что Возьмем произвольное e>0. В качестве d можно взять любое положительное число. Тогда при
Теорема 4. Функция не может иметь двух различных пределов в одной точке. Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при, то и произведение имеет предел при Теорема 7. Если функции f(x) и g(x) имеют предел при Х стремящийся к А, то и их частное имеет предел при Х стремящийся А, причем предел частного равен частному пределов.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

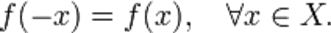
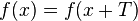
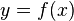 относительно Х. Если оно имеет более чем один корень, то функции обратной к
относительно Х. Если оно имеет более чем один корень, то функции обратной к  не существует.
не существует. , найдется такое положительное число
, найдется такое положительное число  , что для всех Х не равных Х0, и удовлетворяющие условию
, что для всех Х не равных Х0, и удовлетворяющие условию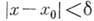 будет верно неравенство
будет верно неравенство 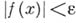
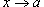 если для каждого
если для каждого  существует такое число
существует такое число  , что
, что 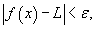 при условии
при условии 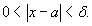




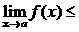
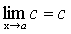
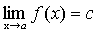

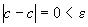
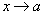 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при