
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие дифференциала функцииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ДИФФЕРЕНЦИАЛ ФУНКЦИИ Понятие дифференциала функции
Пусть функция y = f (x) дифференцируема на отрезке [ a; b ]. Производная функции в некоторой точке х 0 Î [ a; b ] определяется равенством
Итак, приращение дифференцируемой функции y = f (x) может быть представлено в виде суммы двух слагаемых, из которых первое (при f' (х) ≠ 0) линейно относительно D х и при D х ® 0 является бесконечно малой того же порядка малости, что D х. Поэтому говорят, что первое слагаемое является главной частью приращения, линейной относительно Δ x. Второе слагаемое – бесконечно малая величина более высокого порядка, чем Δ x. Дифференциалом функции f (x) в точке х называется главная линейная часть приращения функции. Обозначается d y или df (x). Из определения следует, что dy = f ¢(x)D x. Таким образом, если функция y = f (x) имеет производную f' (x) в точке x, то произведение производной f ' (x) на приращение Δ x аргумента называют дифференциалом функции. Найдем дифференциал функции y = x. В этом случае y ' = (x)' = 1 и, следовательно, dy = dx = Δ x. Значит, дифференциал dx независимой переменной x совпадает с ее приращением Δ x. Поэтому можем записать: dy = f ¢(x) dx. Можно также записать: Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной. Замечание. Из дифференцируемости функции в точке следует существование дифференциала в этой точке. Справедливо и обратное утверждение: для функции y = f (x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)= А. Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.
Геометрический смысл дифференциала
Рассмотрим функцию y = f (x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M (x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δ x, тогда функция получит приращение Δ y = NM 1. Значениям x +Δ x и y + Δ y на кривой y = f (x) будет соответствовать точка M 1(x +Δ x; y +Δ y). Из Δ MNT находим NT = MN ·tg α. Т.к. tg α = f' (x), а MN = Δ x, то NT = f '(x)·Δ x. Но, по определению дифференциала, dy = f '(x)·Δ x, поэтому dy = NT. Таким образом, дифференциал функции f (x), соответствующей данным значениям x и Δ x, равен приращению ординаты касательной к кривой y = f (x) в данной точке х.
Свойства дифференциала.
Если u = f (x) и v = g (x) – функции, дифференцируемые в точке х, то непосредственно из определения дифференциала и таблицы производных следуют следующие свойства: 1) d (u ± v) = (u ± v) ¢dx = u¢dx ± v¢dx = du ± dv. 2) d (uv) = (uv) ¢dx = (u¢v + v¢u) dx = vdu + udv. 3) d (Cu) = Cdu. 4) 4. Дифференциал сложной функции. Инвариантная форма записи дифференциала Найдем выражение для дифференциала сложной функции. Пусть y=f (u), u=g (x) или y = f (g (x)). Тогда по правилу дифференцирования сложной функции: Мы доказали следующую теорему. Теорема. Дифференциал сложной функции y = f (u), для которой u = g (x), имеет тот же вид dy=f '(u) du, какой он имел бы, если бы промежуточный аргумент u был независимой переменной. Иначе говоря, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала. Однако, если х – независимая переменная, то dx = D x, но если х зависит от t, то D х ¹ dx. Таким образом, форма записи dy = f ¢(x)D x не является инвариантной. Примеры.
ФОРМУЛА ТЕЙЛОРА
Теорема Тейлора. 1) Пусть функция f (x) имеет в точке х = а и некоторой ее окрестности производные порядка (n+1) включительно (т.е. все производные функции до порядка n непрерывны и дифференцируемы в этой окрестности). 2) Пусть х – любое значение из этой окрестности, но х ¹ а. Тогда между точками х и а найдется такая точка
Это выражение называется формулой Тейлора, а выражение: Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д. Если в формуле Тейлора положить а = 0, то она запишется в виде
Этот частный случай формулы Тейлора называют формулой Маклорена (Колин Маклорен (1698-1746) шотландский математик)
ПРАВИЛО ЛОПИТАЛЯ Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей. Теорема (правило Лопиталя). Пусть функции f (x) и g (x) определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a; g¢(x) ≠ 0 в этой окрестности и пусть Коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных. Замечание. Формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует. Например, найти Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности0/0 или ∞/∞, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
ПРИЗНАКИ ЭКСТРЕМУМА ФУНКЦИИ
Рассмотрим график непрерывной функции y = f (x), изображенной на рисунке. Значение функции в точке x 1 будет больше значений функции во всех соседних точках как слева, так и справа от x 1. В этом случае говорят, что функция имеет в точке x 1 максимум. В точке x 3 функция, очевидно, также имеет максимум. Если рассмотреть точку x 2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x 2 минимум. Аналогично для точки x 4. Функция y = f (x) в точке x 0 имеет максимум, если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f (x) < f (x 0). Функция y = f (x) имеет минимум в точке x 0, если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f (x)> f (x0). Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции. Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка. Отметим, что точки экстремума носят локальный характер, т.е. если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x 1 имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x 1. В частности, f (x 1) < f (x 4) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близких к точке максимума. Теорема 1. (Теорема Ферма, Необходимое условие существования экстремума.) Если дифференцируемая функция y = f (x) имеет в точке x= x 0 экстремум, то ее производная в этой точке обращается в нуль. ► Пусть для определенности в точке x 0 функция имеет максимум. Тогда при достаточно малых приращениях Δ x имеем f (x 0+ Δ x) < f (x 0), т.е.
Переходя в этих неравенствах к пределу при Δ x → 0 и учитывая, что производная f '(x 0) существует: Так как f ' (x 0) определяет число, то эти неравенства совместны только в том случае, когда f ' (x 0) = 0.◄ Геометрический смысл теоремы Ферма состоит в том, что если в точке x 0 дифференцируемая функция имеет экстремум, то в точке Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры. Пример. Следствие. Таким образом, из приведенного примера и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Обратное утверждение неверно: Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х 3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются стационарными (лат. стоящий, неподвижный) или критическими точками. Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема. Теорема 2. (I достаточный признак экстремума.) Если непрерывная функция b) минимумом, если знак меняется с минуса на плюс: f ' (x) < 0 при x < x 0 и f ' (x) > 0 при x > x 0. ►По условию, Если f ' (х) > 0 при x < x 0 и и f ' (х) < 0 при x > x 0, то это означает, что слева от точки Аналогично доказывается вторая часть теоремы о минимуме.◄
Исследование функции на экстремум может выполняться и с помощью производных высших порядков. Теорема 3. (II достаточный признак экстремума.) Если функция Если f ¢¢(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование. Максимизация прибыли. Пусть Q – количество реализованного товара, R(Q) – функция дохода, C(Q) – функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организация инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой П(Q) = R(Q) – C(Q). В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, необходимо, чтобы предельный доход и придельные издержки были равны. Этот принцип можно записать в виде R '(Q) = C '(Q). Действительно, из необходимого условия экстремума для функции П (Q) следует, что П '(Q) = 0, откуда и получается основной принцип. Пример. Найти максимум прибыли, если доход и издержки определяются следующими формулами: R (Q) = 100 Q – Q 2, C (Q) = Q 3 – 37 Q 2 + 169 Q + 4000. Решение. Прибыль П (Q) = – Q 3 + 36 Q 2 – 69 Q – 4000. Приравнивая производную функцию прибыли к нулю, получаем уравнение Q 2 – 24 Q + 23 = 0. Корни этого уравнения Q 1 = 1, Q 2 = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23; П max =1290.
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат. Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном графике функции Термин асимптота введен древнегреческим ученым Аполлонием Пергским при изучении гиперболы и происходит от греческого слова «асимтотос», означающего «несовпадающий». Хотя кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую. Следует отметить, что не любая кривая имеет асимптоту. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой. Различают три вида асимптот: вертикальные, горизонтальные и наклонные. Вертикальные асимптоты Вертикальной асимптотой графика функции Вертикальные асимптоты следует искать в точках разрыва функции или на концах её области определения, если концы не равны График непрерывной на всей числовой прямой функции вертикальных асимптот не имеет. Горизонтальные асимптоты Если Наклонные асимптоты Поскольку асимптота – это прямая, то если кривая Теорема. Прямая y = kx + b служит наклонной асимптотой при x → ∞ для графика функции Замечание 1. Теорема показывает, что для нахождения наклонных асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая наклонных асимптот не имеет. Замечание 2. Горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0. Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот. При отыскании асимптот, как правило, рассматривают лишь два случая: вертикальные и наклонные. Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
ДИФФЕРЕНЦИАЛ ФУНКЦИИ Понятие дифференциала функции
Пусть функция y = f (x) дифференцируема на отрезке [ a; b ]. Производная функции в некоторой точке х 0 Î [ a; b ] определяется равенством
Итак, приращение дифференцируемой функции y = f (x) может быть представлено в виде суммы двух слагаемых, из которых первое (при f' (х) ≠ 0) линейно относительно D х и при D х ® 0 является бесконечно малой того же порядка малости, что D х. Поэтому говорят, что первое слагаемое является главной частью приращения, линейной относительно Δ x. Второе слагаемое – бесконечно малая величина более высокого порядка, чем Δ x. Дифференциалом функции f (x) в точке х называется главная линейная часть приращения функции. Обозначается d y или df (x). Из определения следует, что dy = f ¢(x)D x. Таким образом, если функция y = f (x) имеет производную f' (x) в точке x, то произведение производной f ' (x) на приращение Δ x аргумента называют дифференциалом функции. Найдем дифференциал функции y = x. В этом случае y ' = (x)' = 1 и, следовательно, dy = dx = Δ x. Значит, дифференциал dx независимой переменной x совпадает с ее приращением Δ x. Поэтому можем записать: dy = f ¢(x) dx. Можно также записать: Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной. Замечание. Из дифференцируемости функции в точке следует существование дифференциала в этой точке. Справедливо и обратное утверждение: для функции y = f (x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)= А. Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

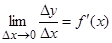 . Тогда по свойству предела можно записать:
. Тогда по свойству предела можно записать:  , где a ® 0, при D х ® 0 т.е. является бесконечно малой,
, где a ® 0, при D х ® 0 т.е. является бесконечно малой,  остается постоянной величиной при D х ® 0. Следовательно:
остается постоянной величиной при D х ® 0. Следовательно: .
. .
.
 .
. . Следовательно, по определению
. Следовательно, по определению 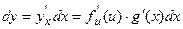 , но g '(x) dx = du, поэтому dy= f '(u) du.
, но g '(x) dx = du, поэтому dy= f '(u) du.

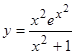
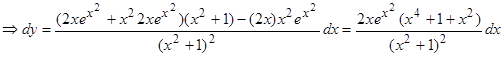
 , что справедлива формула:
, что справедлива формула:
 называется остаточным членом в форме Лагранжа.
называется остаточным членом в форме Лагранжа. ,
, 
 или
или  . Тогда предел отношения функций при х® а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует
. Тогда предел отношения функций при х® а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует 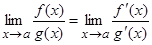 (1)
(1) . Этот предел существует
. Этот предел существует  . Но отношение производных (1 + cos x) / 1 = 1 + cos x при x → ∞ не стремится ни к какому пределу.
. Но отношение производных (1 + cos x) / 1 = 1 + cos x при x → ∞ не стремится ни к какому пределу. . Но тогда
. Но тогда

 , а следовательно предел, стоящий слева, не зависит от того как Δ x → 0, получаем: при Δ x → – 0 f' (x 0) ≥ 0, а при Δ x → + 0 f' (x 0) ≤ 0.
, а следовательно предел, стоящий слева, не зависит от того как Δ x → 0, получаем: при Δ x → – 0 f' (x 0) ≥ 0, а при Δ x → + 0 f' (x 0) ≤ 0. касательная к графику функции y = f (x) параллельна оси абсцисс. Теорема неверна, если функция рассматривается на отрезке.
касательная к графику функции y = f (x) параллельна оси абсцисс. Теорема неверна, если функция рассматривается на отрезке. y = | x |. Функция не имеет производной в точке x = 0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y (0) = 0, а при всех x ≠ 0 y > 0.
y = | x |. Функция не имеет производной в точке x = 0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y (0) = 0, а при всех x ≠ 0 y > 0. дифференцируема в некоторой окрестности стационарной точки
дифференцируема в некоторой окрестности стационарной точки 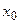 и при переходе через неё (слева направо) производная имеет противоположные знаки, то
и при переходе через неё (слева направо) производная имеет противоположные знаки, то 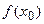 является экстремумом функции, причем: а) максимумом, если знак меняется с плюса на минус: f ' (x) > 0 при x < x 0 и f ' (x) < 0 при x > x 0;
является экстремумом функции, причем: а) максимумом, если знак меняется с плюса на минус: f ' (x) > 0 при x < x 0 и f ' (x) < 0 при x > x 0; в точке x 0 функция имеет максимум.
в точке x 0 функция имеет максимум. ,
, 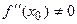 , то в этой точке функция имеет экстремум, причем максимум, если
, то в этой точке функция имеет экстремум, причем максимум, если  , и минимум, если
, и минимум, если  .
. Прямая называется асимптотой графика функции
Прямая называется асимптотой графика функции  . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.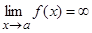 хотя бы при одном из условий x → а – 0 или x → а + 0.
хотя бы при одном из условий x → а – 0 или x → а + 0. .
. , то
, то  – горизонтальная асимптота кривой
– горизонтальная асимптота кривой 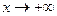 , левая при
, левая при 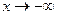 и двусторонняя, если пределы при
и двусторонняя, если пределы при  равны).
равны).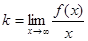 ,
,  .
.


