
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление.Содержание книги Поиск на нашем сайте Дифференциальное исчисление. Производная. Пусть функция у=f(x) определена в некоторой окрестности V(x0) точки х0. Дадим значению аргумента х0 приращение ∆х=х-х0 такое, что Dх≠0 и точка х=х0+DхÎV(x0). Тогда функция получит приращение Dу=f(x)-f(x0) или Dу=f(х0+Dх)-f(x0) – приращение функции. Рассмотрим предел отношения приращения функции к приращению аргумента при приближении точки х к х0. Определение. Если существует предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, то этот предел называется производной функции в точке х0:
Или Обозначения: Если предел Пример. Найдем по определению производную функций: 1) f(x)=С, f¢(x)=0. 2) f(x)=cos x
= 3) f(x)=sin x
=
4) f(x)=xn (nÎN) 1. Случай n=1. f(x)=x 2. n=2,3,… Воспользуемся формулой бинома Ньютона:
=
(xn)¢=nxn-1. 5) f(x)=ax
Введем замену, t=a∆x-1→0 при ∆х→0. Тогда а∆х=t+1; ∆x=loga(t+1)= Получаем: = Т.о. 6) f(x)=logax
В силу непрерывности функции f(x)=logax f(x)=logax имеем
Т.о.
1) f(x)=sign x= В точке х0=0 нет производной f(0+Dx)-f(0)=
2) f(x)=êхê- в точке х0=0 нет производной (в положительной полуплоскости f¢(x)=х, в отрицательной - f¢(x)=-х). (График) f(0+Dx)-f(0)= Геометрический смысл производной. Задача о касательной к кривой. Пусть на плоскости задана непрерывная кривая L, описываемая уравнением у=f(x). Требуется найти уравнение касательной к ней в точке М0(х0,у0). Определение. Касательной к кривой L в точке х0 называется предельное положение секущей М0М, проходящей через точку М0 и некоторую другую точку М, лежащую на кривой L, когда точка М вдоль кривой произвольным образом стремиться к совпадению с точкой М0, т.е. при Δх→0. Дадим аргументу х0 приращение Δх такое, что Dх≠0 и перейдем на кривой от точки М0(х0,f(x0)) к точке М(х0+Δx, f(x0+Δx)) или М(х0+Δx,у0+Δу) (Dу=f(x0+Δx)-f(x0), у0=f(x0)) и проведем секущую М0М. Она имеет уравнение у-у0=k(Dх)(x-x0) (1) Угловой коэффициент секущей М0М можно найти из ∆ М0МN:
Равенство (2) справедливо при любом расположении кривой L и при любом Расположении точки М относительно точки М0 (справа или слева). При Dх→0 расстояние êМ0Мê→0. Действительно, в силу непрерывности функции f(x) в точке х0 будет Тогда угловой коэффициент касательной
Т.о., если у функции f(x) в точке x0, то уравнение касательной к графику функции y=f(x) в точке М0(х0,у0) будет иметь вид: у-у0= Т.о. получили геометрический смысл производной: производная Если у функции у=f(x) в точке х0 существует бесконечная производная, т.е.
Запишем уравнение секущей М0М у-у0=k(Dх)(x-x0) в виде: Переходя в этом соотношении к пределу при Dх→0, получим: х-х0=0Þ х=х0 (4) (4) -уравнение касательной к графику функции у=f(x) в точке М0 в случае, когда
Односторонние производные. 1) Пусть функция y=f(x) определена в точке х0 и некоторой правосторонней окрестности этой точки u+(x0). Если существует конечный или бесконечный (определенного знака) предел
то этот предел называется соответственно конечной или бесконечной правосторонней производной функции f(x) в точке х0 и обозначается 2) Пусть функция y=f(x) определена в точке х0 и некоторой левосторонней окрестности этой точки u-(x0). Если существует конечный или бесконечный (определенного знака) предел
то этот предел называется соответственно конечной или бесконечной левосторонней производной функции f(x) в точке х0 и обозначается Об односторонних производных функции y=f(x) в точке х0 можно говорить и в случае, когда эта функция определена в точке х0 и в некоторой окрестности u(x0) точки х0 (т.е. f(x) определена одновременно и в u+(x0), и в u-(x0)). Для функции y=f(x), определенной в u(x0), справедливо следующее утверждение: Для того, чтобы у функции f(x) в точке х0 существовала обычная (т.е. двусторонняя) производная, необходимо и достаточно, чтобы в точке х0 существовали одновременно В случае, если у функции y=f(x) в точке х0 существуют одновременно Пример. f(x)=êхê, х0=0. Dу=f(x0+Dx)-f(x0)=f(0+Dx)-f(0)=ê0+Dxê-ê0ê=êDxê Если Dx>0, то Dу=Dx, следовательно Если Dx<0, то Dу=-Dx, следовательно
Дифференцируемые функции. Пусть функция y=f(x) определена в некотором промежутке Х и точка х0ÎХ. Дадим значению аргумента х0 приращение Δх такое, что Δх≠0 и х0+ΔхÎХ. Пусть Δу=f(х0+Δх)-f(х0) – приращение функции. Определение. Функция y=f(x) называется дифференцируемой в точке х0, если приращение Δу этой функции в точке х0 может быть представлено в виде Δу=А×Dх+a×Dх (1) Где А – некоторое число, не зависящее от Δх, а a - функция аргумента Δх такая, что a(Δх)→0 при Δх→0 (т.е. б.м. при Δх→0). В точке Δх=0 функция a(Δх) может принимать любое значение. Для определенности можно, например, положить a(0)=0. Пример. f(x)=х2. f(х0+Δх)-f(х0)=(х0+Δх)2-х02=2х0Dх+(Dх)2 А=2х0, a(Δх)=(Dх)2→0 при Δх→0 d(f(x0))=2x0. Теорема. Для того, чтобы функция y=f(x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы она имела в этой точке конечную производную. Доказательство. Необходимость. Пусть функция y=f(x) дифференцируема в точке х0. Докажем, что существует конечная производная Т.к. y=f(x) дифференцируема в точке х0, то приращение Dу этой функции в точке х0, соответствующее приращению аргумента Dх, можно представить в виде: Δу=А×Dх+a×Dх, где a(Δх)→0 при Δх→0. Предположим, что Dх≠0 и разделим обе части равенства на Dх: Переходя к пределу при Δх→0, находим А это и означает, что существует конечная Достаточность. Пусть функция y=f(x) имеет в точке х0 конечную производную. Покажем, что f(x) дифференцируема в точке х0. Т.к. существует конечная Положим Полученное выражение для Δу совпадает с представлением Δу=А×Dх+a×Dх, если обозначить через А не зависящее от Dх число Замечание. Из теоремы следует, что дифференцируемость функции у=f(x) в точке х0 равносильна существованию в этой точке конечной производной Правила дифференцирования. Пусть функции U=U(x), V=V(x) дифференцируемы в точке х0, тогда функции U±V, UV, CU, U/V также дифференцируемы в этой точке и справедливы равенства: 1. 2. 3. 4. Доказательство. 2) Дадим х приращение Dх. Тогда функции u(x) и v(x) получат соответственно приращения Du и Dv, их новыми значениями будут u(x)+Du и v(x)+Dv (т.к. Du=u(x+Dx)-u(x), Dv=v(x+Dx)-v(x)) Пусть y=u±v, тогда Dy=[(u(x)+Du)±(v(x)+Dv)]-[u(x)±v(x)]=u(x)+Du±v(x)±Dv-u(x) 3. Приращение функции у=UV: у+∆у=(u(x)+∆u)(v(x)+∆v)-uv=u(x)v(x)+∆uv(x)+u(x)∆v+∆u∆v-u(x)v(x)= =∆uv(x)+u(x)∆v+∆u∆v Рассмотрим отношение приращений функции и аргумента:
Т.к. функция u=u(x) дифференцируема в точке х, то она непрерывна, следовательно (или Т.о. Доказательство 4. Представим функцию у=
Тогда Следствие 1. Постоянный множитель можно выносить за знак производной.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведения производной каждого из сомножителей на все остальные, например:
Таблица производных. 1. С¢=0 (С=const) 2. 3. 4. 5. 7. 9. 11. Пример. Вывод производной функции у=tg x и у=ctg x, используя правило 4. Пример. Дифференцирование степенной функции. Покажем, что хα=
Производная степенно-показательной функции у=f(x)g(x). Рассмотрим логарифмическую производную, т.е. производную логарифмической функции: Тогда ln y=g(x)lnf(x). Дифференцируя, получим
Т.к. у=f(x)g(x), получаем Т.е. для того, чтобы найти производную степенно-показательной функции надо сначала дифференцировать ее как степенную, а потом как показательную функцию и полученные результаты сложить. Пример. Найти производную функции у=хх. Дифференциал функции. Подход к дифференциальному исчислению связан с аппроксимацией (приближением) функций. Пусть функция y=f(x) определена в некотором промежутке Х и точка х0ÎХ. Дадим значению аргумента х0 приращение Δх такое, что Δх≠0 и х0+ΔхÎХ. Пусть Δу=f(х0+Δх)-f(х0) – приращение функции в точке х0, соответствующее приращению Dх аргумента. Если функция f(x) имеет в точке х0 конечную производную Δу= где α(Dx)→0 при Dx→0. Если Т.к. в этом случае Второе слагаемое a(Dх)×Dх правой части (1) при Dx→0 является бесконечно малой более высокого порядка, чем Dх, т.к. Определение. Д ифференциалом функции у=f(х) в точке х0 называется произведение производной, вычисленной в этой точке, на приращение Dх аргумента: dy= Пример. Найти дифференциал функции у=х. dy=dx=(x)¢×Dx=Dx. Т.о. полагают, что дифференциал независимой переменной равен ее приращению, т.е. dx=Dx. (это своего рода соглашение). Тогда вместо равенства (2) можно записать dy=
Рассмотрим формулу Δу= Если
Значит в случае, когда Приближенное равенство (5) тем точнее, чем меньше Dх. Формулой (5) пользуются в приближенных вычислениях, т.к. структура дифференциала функции dy проще структуры ее приращения Dу. Пример. у=х3. Dу=(х+Dх)3-х3=3х2×Dх+3х×(Dх)2+(Dх)3, а dy=3х2 Dх Если взять х=2, Dх=0,01, то Dу=3×4×0,01+3×2×0,0001+0,000001=0,120601, а dy=3×4 0,01=0,12. Т.о. абсолютная ошибка údy-Dуú=0,000601, относительная ошибка
Пример. Найти производную функции
Чтобы найти Тогда В рассмотренном примере Аналогично, считая, что функция
Находим
Дифференциальное исчисление. Производная. Пусть функция у=f(x) определена в некоторой окрестности V(x0) точки х0. Дадим значению аргумента х0 приращение ∆х=х-х0 такое, что Dх≠0 и точка х=х0+DхÎV(x0). Тогда функция получит приращение Dу=f(x)-f(x0) или Dу=f(х0+Dх)-f(x0) – приращение функции. Рассмотрим предел отношения приращения функции к приращению аргумента при приближении точки х к х0. Определение. Если существует предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, то этот предел называется производной функции в точке х0:
Или Обозначения: Если предел Пример. Найдем по определению производную функций: 1) f(x)=С, f¢(x)=0. 2) f(x)=cos x
= 3) f(x)=sin x
=
4) f(x)=xn (nÎN) 1. Случай n=1. f(x)=x 2. n=2,3,… Воспользуемся формулой бинома Ньютона:
=
(xn)¢=nxn-1. 5) f(x)=ax
Введем замену, t=a∆x-1→0 при ∆х→0. Тогда а∆х=t+1; ∆x=loga(t+1)= Получаем: = Т.о. 6) f(x)=logax
В силу непрерывности функции f(x)=logax f(x)=logax имеем
Т.о.
1) f(x)=sign x= В точке х0=0 нет производной f(0+Dx)-f(0)=
2) f(x)=êхê- в точке х0=0 нет производной (в положительной полуплоскости f¢(x)=х, в отрицательной - f¢(x)=-х). (График) f(0+Dx)-f(0)=
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |

 (1)
(1) (2)
(2) ,
,  ,
,  ,
,  .
. конечен, то производная называется конечной, если он бесконечен, то производная называется бесконечной. Процесс вычисления производных функций называется дифференцированием; точка х0, в которой вычисляется производная, называется точкой дифференцирования.
конечен, то производная называется конечной, если он бесконечен, то производная называется бесконечной. Процесс вычисления производных функций называется дифференцированием; точка х0, в которой вычисляется производная, называется точкой дифференцирования. =
=  =
=  =
= =-2sin x0·
=-2sin x0·  =-sin x0. Т.о.
=-sin x0. Т.о. 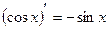
 =
= 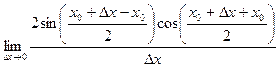 =
= =-2×
=-2× 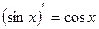


 =
= →
→  при Dх→0,
при Dх→0, 

 =
=  =
= 

 =
= 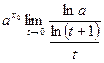 =
=  =
= =
=  =
= 
 в частности,
в частности, 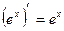
 =
= 


 Примеры функций, не имеющих производную.
Примеры функций, не имеющих производную.
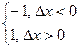
 =
=  - нет предела при Dх→0
- нет предела при Dх→0 ,
,  ,
, 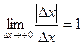 Þ нет предела при Dх→0
Þ нет предела при Dх→0 =tgφ=
=tgφ=  (2)
(2) =0. Тогда êМ0Мê=
=0. Тогда êМ0Мê= 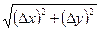 →0 при Dх→0 и точка М по кривой будет стремиться к совпадению с точкой М0, секущая М0М будет стремиться принять свое предельное положение М0Т, tgj→tga, Dx→0
→0 при Dх→0 и точка М по кривой будет стремиться к совпадению с точкой М0, секущая М0М будет стремиться принять свое предельное положение М0Т, tgj→tga, Dx→0 k=
k=  =
=  =
=  =¥.
=¥.



 ,
, .
.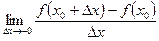 ,
, .
. .
. .
.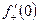 ≠
≠ 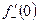 , значит обычной производной у функции f(x)=êхê в точке 0 нет.
, значит обычной производной у функции f(x)=êхê в точке 0 нет. =0. Следовательно,
=0. Следовательно, 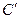 =0, где С=const
=0, где С=const
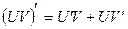
 (V≠0)
(V≠0) 
 v(x)=Du±Dv
v(x)=Du±Dv =
= 
 , т.е.
, т.е.  =0.
=0. =0)
=0) =
=  ч.т.д.
ч.т.д. в виде у=u
в виде у=u  и сведем к предыдущему случаю.
и сведем к предыдущему случаю. =
=  =-
=-  =
= 

 ч.т.д.
ч.т.д.
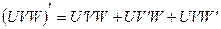
 =nxn-1
=nxn-1 


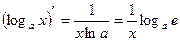

 8.
8. 
 10.
10. 
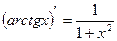 12.
12. 

 =eαlnx
=eαlnx = eαlnx
= eαlnx  =xα·α·
=xα·α·  =αxα-1 ч.т.д.
=αxα-1 ч.т.д. (относительная скорость изменения функции или темп изменения функции).
(относительная скорость изменения функции или темп изменения функции). .
.
 , то приращение Δу этой функции в точке х0 может быть представлено в виде
, то приращение Δу этой функции в точке х0 может быть представлено в виде

 (4)
(4) Þ
Þ  =1/
=1/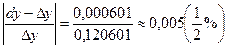
 циклоида
циклоида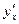 =
= 
 замечаем, что функция
замечаем, что функция  , где ψ1(t)=
, где ψ1(t)=  или ψ1(t)=
или ψ1(t)=  .
. =
=  =
= 

 , где ψ2(t)=
, где ψ2(t)=  =
=  =
=  и т.д.
и т.д.



