
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл дифференциала.Содержание книги
Поиск на нашем сайте
Пусть графиком функции y=f(x), хÎХ является кривая L. Пусть значению аргумента х0 соответствует некоторая точка М0. Проведем к кривой L в точке М0 касательную М0Т. Для углового коэффициента касательной справедлива формула При переходе от х0 к х0+Dх ордината касательной получит приращение NK=Dx×tg a= Т.о., dy – это это приращение ординаты точки, лежащей на касательной к кривой L в точке М0, при переходе от х0 к х0+Dх. Замена приращения функции Dу дифференциалом dy равносильна переходу от заданной функциональной зависимости у от х (y=f(x)) к линейной зависимости у от х в достаточно малой окрестности точки х0. Полученная при такой замене погрешность оказывается бесконечно малой более высокого порядка, чем приращение аргумента. Основные свойства и правила дифференцирования. Т.к. дифференциал dy функции y=f(x) получается умножением производной этой функции Рассмотрим формулу
Аналогичным образом получим остальные формулы: 1) dС=0 2) d(cu)=cdu 3) d(u±v)=du±dv 4) d(uv)=vdu+udv 5) d 6) d(xr)=rxr-1dx 7) 9) 11) 13) 15) 17) 19) 21) 23) Дифференциал сложной функции. Рассмотрим сложную функцию у=f(j(x)). Пусть даны функции f и φ: Пусть функция u=j(x) имеет конечную производную Т.к. у=f(j(x)) – функция независимой переменной х, определенная на промежутке Х, то, по определению дифференциала: dy= По правилу дифференцирования сложной функции
Подставляя это выражение для dy= По определению дифференциала: du= Окончательно получаем: dy= Сравнивая соотношения (*) и (**) заметим, что дифференциал сложной функции у=f(j(x)) через промежуточную переменную u выражается в той же форме, как и через независимую переменную х.
В этом состоит свойство инвариантности (неизменяемости) формы дифференциала. Пример. у= Положим х=sin t, tÎ Тогда dx=cos t×dt, dy=-sin t×dt
Производные высших порядков. Пусть функция у=f(x) определена в некотором промежутке Х и в каждой точке этого промежутка имеет конечную производную Назовем Если существует производная от Вторая производная Производная от второй производной называется производной 3-го порядка (третьей производной): Аналогично вводятся четвертая, пятая и т.д. производные от функции у=f(x). Обозначения производной n–го порядка: Пример. 1) y=ln x, xÎ(0,+¥)
Допустим, что тогда Т.о. 2) y=sin x, хÎ(-¥,+¥)
Допустим, что Тогда Т.о. 3. Пусть функции u(x) и v(x) в некотором промежутке Х имеют конечные производные всех порядков до n включительно. Рассмотрим функцию у(х)=u(x)±v(x).
Допустим, что Тогда Т.о. Формула Лейбница для производной n-го порядка от произведения двух функций. Теорема. (б/д)Пусть функции u(x) и v(x) в некотором промежутке Х имеют конечные производные всех порядков до n включительно. Тогда функция у(х)=u(x)×v(x) имеет в промежутке Х конечные производные всех порядков до n включительно, причем (Доказывается, аналогично выводу формулы Пример. у=х2ех. Вычислить у(100). Здесь u(x)=ех, v(x)= х2. у(100)=(ех×х2)(100)= =(ех)(100)×х2+100×(ех)(99)×
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.7 (0.009 с.) |


 .
.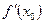 ×Dx=dy.
×Dx=dy. на дифференциал независимой переменной dx (dy=
на дифференциал независимой переменной dx (dy=  ×dx), то операции на вычисление производной и дифференциала, с точки зрения техники вычислений, почти не отличаются друг от друга. Это позволяет из формул для производных получить соответствующие формулу для дифференциалов.
×dx), то операции на вычисление производной и дифференциала, с точки зрения техники вычислений, почти не отличаются друг от друга. Это позволяет из формул для производных получить соответствующие формулу для дифференциалов.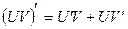 . Умножим обе части на dx, получим:
. Умножим обе части на dx, получим: или
или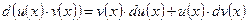 d(u±v)=du±dv
d(u±v)=du±dv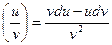
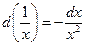 8)
8) 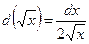
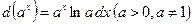 10)
10) 
 12)
12) 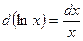
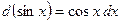 14)
14) 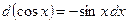
 16)
16) 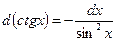
 18)
18) 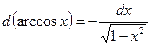
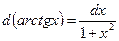 20)
20) 
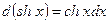 22)
22) 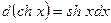
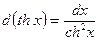 24)
24) 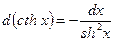
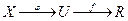 . Т.е. функция y=f(u) определена в промежутке U, а функция u=j(х) определена в промежутке Х и если хÎХ, то j(х)ÎU. Тогда для хÎХ имеет смысл выражение у=f(j(x)) – сложная функция.
. Т.е. функция y=f(u) определена в промежутке U, а функция u=j(х) определена в промежутке Х и если хÎХ, то j(х)ÎU. Тогда для хÎХ имеет смысл выражение у=f(j(x)) – сложная функция. на промежутке Х, а функция у=f(u) имеет конечную производную
на промежутке Х, а функция у=f(u) имеет конечную производную  на промежутке U.
на промежутке U. dx (*)
dx (*)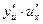
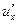 dx
dx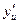 du (**)
du (**)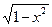 , xÎ(-1,1)
, xÎ(-1,1)  .
.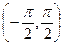 . Тогда у=
. Тогда у=  .
.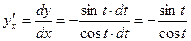 - получили лишь другое выражение для вычисленной выше производной.
- получили лишь другое выражение для вычисленной выше производной.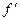 (х). Тогда производная сама является функцией от х на промежутке Х.
(х). Тогда производная сама является функцией от х на промежутке Х.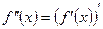 ,
, 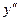 ,
,  .
.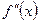 также может иметь производную на промежутке Х.
также может иметь производную на промежутке Х.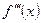 ,
, 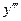 ,
,  .
. ,
, 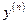 ,
,  .
.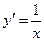 ,
, 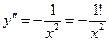 ,
, 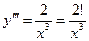
 ,
,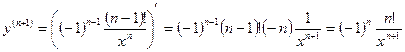
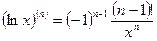 верна
верна 
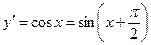 ,
, 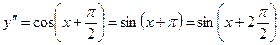
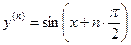

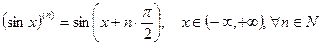
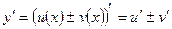
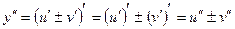

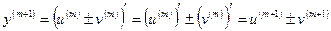

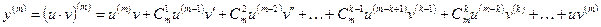 , m=1,2,…,n
, m=1,2,…,n ).
).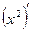 +
+ 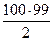 ×(ех)(98)×
×(ех)(98)× 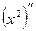 +0= ех×х2+200ех×х+9900 ех.
+0= ех×х2+200ех×х+9900 ех.


