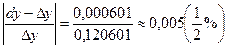Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная обратной функции.Содержание книги Поиск на нашем сайте Если у=f(х) – взаимно однозначное отображение, т.е. является инъекцией ( Можно определить новую функцию: f-1:B→A, x=f-1(y)–обратная функция, относительно f. Пусть функцияу=f(x) определена в промежутке áa,bñ и является там строго монотонной и непрерывной. Тогда у функции у=f(x) существует обратная функция х=j(у), определенная в промежутке áp,qñ, причем эта функция в промежутке áp,qñ также строго монотонна и непрерывна. (áp,qñ - множество значений, принимаемых функцией у=f(x) на промежутке áa,bñ). Теорема. Пусть 1) функцияу=f(x) определена в промежутке áa,bñ и является там строго монотонной и непрерывной; 2)функцияу=f(x) имеет конечную ненулевую производную в точке х0Îáa,bñ. Тогда обратная функция х=j(у)=f-1(у) также имеет производную в соответствующей точке у0=f(x0)Îáp,qñ и справедлива формула: Если у=f(x) имеет ненулевую производную в каждой точке, то Доказательство. По условию Придадим у0 приращение Dу≠0 такое, что точка у0+DуÎáp,qñ. Тогда функция х=j(у) получит приращение Dх=j(у0+Dу)-j(у0). В силу строгой монотонности функции х=j(у) Dх≠0, если Dу≠0. В силу непрерывности функции х=j(у) Dх®0, если Dу®0. Имеем очевидное равенство Т.к. по условию Геометрический смысл формулы
Пример. 1) у=arcsin x, хÎ(-1,1) (уÎ Эта функция является обратной для функции x=sin y, которая для уÎ Тогда функция у=arcsin x дляхÎ(-1,1) имеет конечную производную, причем
2) у=arcоs x, хÎ(-1,1) (уÎ(0,p)) Эта функция является обратной для функции x=соs y, которая для уÎ(0,p) имеет конечную отличную от нуля производную. Тогда функция у=arccos x дляхÎ(-1,1) имеет конечную производную, причем
3) у=arctg x, хÎ(-¥,+¥) (уÎ Эта функция является обратной для функции x=tg y, которая для уÎ Тогда функция у=arctg x дляхÎ(-¥,+¥) имеет конечную производную, причем
3) у=arcсtg x, хÎ(-¥,+¥) (уÎ(0,p)) Эта функция является обратной для функции x=сtg y, которая для уÎ(0,p) имеет конечную отличную от нуля производную. Тогда функция у=arcсtg x дляхÎ(-¥,+¥) имеет конечную производную, причем
Дифференцирование функций, заданных неявно. Рассмотрим функцию F(x,y)=0 Для нахождения ее производной дифференцируют обе части тождества, рассматривая у как функцию от х. Получим тождество Φ(х,у, Пример. Найти производную функции хlny-ylnx=9 Дифференциал функции. Подход к дифференциальному исчислению связан с аппроксимацией (приближением) функций. Пусть функция y=f(x) определена в некотором промежутке Х и точка х0ÎХ. Дадим значению аргумента х0 приращение Δх такое, что Δх≠0 и х0+ΔхÎХ. Пусть Δу=f(х0+Δх)-f(х0) – приращение функции в точке х0, соответствующее приращению Dх аргумента. Если функция f(x) имеет в точке х0 конечную производную Δу= где α(Dx)→0 при Dx→0. Если Т.к. в этом случае Второе слагаемое a(Dх)×Dх правой части (1) при Dx→0 является бесконечно малой более высокого порядка, чем Dх, т.к. Определение. Д ифференциалом функции у=f(х) в точке х0 называется произведение производной, вычисленной в этой точке, на приращение Dх аргумента: dy= Пример. Найти дифференциал функции у=х. dy=dx=(x)¢×Dx=Dx. Т.о. полагают, что дифференциал независимой переменной равен ее приращению, т.е. dx=Dx. (это своего рода соглашение). Тогда вместо равенства (2) можно записать dy=
Рассмотрим формулу Δу= Если
Значит в случае, когда Приближенное равенство (5) тем точнее, чем меньше Dх. Формулой (5) пользуются в приближенных вычислениях, т.к. структура дифференциала функции dy проще структуры ее приращения Dу. Пример. у=х3. Dу=(х+Dх)3-х3=3х2×Dх+3х×(Dх)2+(Dх)3, а dy=3х2 Dх Если взять х=2, Dх=0,01, то Dу=3×4×0,01+3×2×0,0001+0,000001=0,120601, а dy=3×4 0,01=0,12. Т.о. абсолютная ошибка údy-Dуú=0,000601, относительная ошибка
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

 х1≠х2
х1≠х2  f(x1)≠f(x2)) и сюръекцией (отображение «на») (f(A)=B или
f(x1)≠f(x2)) и сюръекцией (отображение «на») (f(A)=B или 
 такое, что y=f(x)). (f:X→Y; φ= f-1:Y→X)
такое, что y=f(x)). (f:X→Y; φ= f-1:Y→X) . или
. или 
 или
или 
 0.
0. . Перейдем в этом равенстве к пределу при Dу®0. Получим:
. Перейдем в этом равенстве к пределу при Dу®0. Получим: 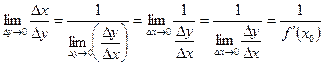
 . Тогда существует и
. Тогда существует и  . Ч.т.д.
. Ч.т.д. является тангенсом угла α наклона касательной к кривой у=f(x) к оси Ох, то
является тангенсом угла α наклона касательной к кривой у=f(x) к оси Ох, то  - тангенс угла наклона β той же касательной к оси Оу.
- тангенс угла наклона β той же касательной к оси Оу.
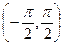 )(График)
)(График)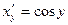 .
.
 (перед радикалом взят знак «+», т.к. cos y>0 для уÎ
(перед радикалом взят знак «+», т.к. cos y>0 для уÎ  , хÎ(-1,1).
, хÎ(-1,1).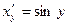 .
.
 (перед радикалом взят знак «+», т.к. sin y>0 для уÎ (0,p)). Т.о.
(перед радикалом взят знак «+», т.к. sin y>0 для уÎ (0,p)). Т.о.  , хÎ(-1,1).
, хÎ(-1,1). .
.
 . Т.к. tg y=x, то получаем
. Т.к. tg y=x, то получаем 
 , хÎ(-¥,+¥).
, хÎ(-¥,+¥). .
.
 . Т.к. сtg y=x, то получаем
. Т.к. сtg y=x, то получаем 
 , хÎ(-¥,+¥).
, хÎ(-¥,+¥).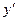 )=0, из которого получаем производную
)=0, из которого получаем производную  , то приращение Δу этой функции в точке х0 может быть представлено в виде
, то приращение Δу этой функции в точке х0 может быть представлено в виде

 (4)
(4) Þ
Þ  =1/
=1/