
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 11. Производная и дифференциал.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МАТЕМАТИКА
Тема 11. Производная и дифференциал. Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица неопределенных интегралов. Тема 13. Определенный интеграл, его свойства. Формула Ньютона – Лейбница. Тема 14. Несобственные интегралы. Несобственные интегралы с бесконечными пределами интегрирования. Несобственные интегралы от разрывных функций. Тесты. Литература
Тема 11. Производная и дифференциал. Приращение аргумента, приращение функции.  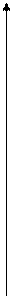 Пусть функция у= f(х) определена в точке х0 и некоторой ее окрестности, придадим точке х0 приращение Δх и получим точку х0+Δх, значение функции в этой точке – f(х0+Δх). Разность значений f (х0+Δх) – f(х0) называется приращением функции, обозначается приращение функции Δf или Δу, т.е. Δf=f(х0+Δх) – f(х0). Рис. 1 Пусть функция у= f(х) определена в точке х0 и некоторой ее окрестности, придадим точке х0 приращение Δх и получим точку х0+Δх, значение функции в этой точке – f(х0+Δх). Разность значений f (х0+Δх) – f(х0) называется приращением функции, обозначается приращение функции Δf или Δу, т.е. Δf=f(х0+Δх) – f(х0). Рис. 1
у Рис.1
Δу
х0 х0 + Δх Производная функция у = f(х), в точке х0 определяется как предел отношения приращения функции Δу к приращению аргумента Δх, при стремлении Δх к нулю. f `(x0) = lim (Δf/Δx). Этот предел будет иметь конечное значение, если только и числитель стремиться к нулю (приращение функции Δf→0). Производная имеет смысл скорости изменения какого – либо показателя. Дифференциал определяется как главная линейная часть приращения функции. Дифференциал показывает, как изменялась бы величина, если бы скорость ее изменения была бы постоянной. Дифференциал для функции у=f(х) обозначается через dy или df. Вычисляется он по формуле dy=f `(x)dx, где f ` (x) – производная функция f(x), а dx – число равное приращению независимой переменной (аргумента) ∆х. Для вычисления производной выведены правила нахождения производной и таблицы производных элементарных функций. Функция, имеющая производную в точке х, называется дифференцируемой в этой точке. Если функция имеет производную в каждой точке интервала, то она называется дифференцируемой в интервале. Правила дифференцирования функций. Пусть U(х) и V(х) дифференцируемы в точке х. 1. (U(x) + V(x))` = U`(x) + V`(x) 2. (U(x) * V(x))` = U`(x) * V`(x) + V`(x) * U`(x) 3. (C*U(x))` = CU`(x), C - const
4. (U(x) / V(x))` = [U`(x) * V(x) - V`(x) * U(x)]/ V2(x) Таблица производных. 1. C` = 0, C – const. 2. x` = 1 3. (xα)` = α xα – 1, α Є R 4. (ax)` = ax lnx, a>0, a≠1 5. (ln x)` = 1/x 6. (sin x)` = cos x 7. (cos x)` = - sin x 8. (tg x)` = 1/(cos x)2 9. (ctg x)` = - 1/(sin x)2 10. (arcsin x)` = 1/ 11. (arccos x)` = - 1/ 12. (arctg x)` = 1/(1 + x2) 13. (arcctg x)` = - [1/(1 + x2)] правила для нахождения дифференциала можно написать самим, умножив соответствующее правило взятия производной на dx. Например: d sinx = (sinx)`dx = cosx dx. Пример 1. Найти приращение функции f(x) = x2, если х = 1, ∆х = 0,1 Решение: f(х) = х2, f(х+∆х) = (х+∆х)2 Найдем приращение функции ∆f = f(x+∆x) – f(x) = (x+∆x)2 – x2 = x2+2x*∆x+∆x2 – x2 = 2x*∆x + ∆x2/ Подставим значения х=1 и ∆х= 0,1, получим ∆f = 2*1*0,1 + (0,1)2 = 0,2+0,01 = 0,21 Пример 2. Найти производную функции f(x) = x2, в произвольной точке х по определению производной, т.е. не используя таблицу производных.
Из первого примера ∆f = 2x*∆x+∆x2, подставим, получим
Пример 3. у = 1-х, Найти ∆у при х=2, ∆ = 0,1 Решение: у(х) = 1-х, у(х+∆х) = 1 – (х+∆х), ∆у = у (х+∆х) – у(х) = 1-х - ∆х – (1 – х) = 1-х - ∆х – 1 + х = - ∆х при х = 2, ∆х = 0,1 ∆у = -∆х = -0,1. Пример 4. Найти производную от функции у=3х4 – 2х2 + 1. Решение у` = 3*4х3 – 2*2х + 0 = 12х3 – 4х. Пример 5. Найти производную от функции у = x2 *℮х. Решение: у` = (x2)` *℮х + x2 *(℮х)` = 2x ℮х + x2 *℮х ln℮ ln ℮ = log℮℮ = 1. y` = 2x℮x + x2 * ℮x Пример 6. У = х/(х2+1). Найти у`. Решение у` = [1*(х2+1) – х*2х] / (х2+1)2 = [х2+1 – 2х2] / (x2 +1)2 = (1-x2) / (x2+1)2 Производные от сложных функций. Формула для нахождения производной от сложной функции такова: [f (φ(х))]` = fφ`(φ(x)) * φ`(x) Например: у = (1-х2)3; у`= 3(1 –х2)2 * (-2х) или у = sin2х; у` = 2sinx * cosx. Пример 7. Найти dy, если у = sin 3х Решение dy = у` * dx = (sin3x)` dx = (cos3x) * 3dx = 3 cos3x dx. Пример 8. Найти dy, если у = 2х^2/ Решение: dy = y` * dx = (2x^2)` * dx = 2x^2 ln2 * 2xdx
Производные высших порядков. Пусть мы нашли от функции у = f(х) ее производную у` = f `(х). Производная от этой производной и называется производной второго порядка от функции f(х) и обозначается у`` или f `` (х) или (d2y) / (dx2). Аналогично определяются и обозначаются: производная третьего порядка у``` = f ```(x) = (d3y) / (dx3). производная четвертого порядка уIV = f IV(x) = (d4y) / (dx4).
производная n-oго порядка у(n) = f (n)(x) = (d n y) / (dxn). Пример: у = 5х4 – 3х3 + 2х – 2. Найти у``. Решение. Находим в начале первую производную: у` = 20х3 – 9х2 +2, потом вторую от первой производной: у`` = 60х2 – 18х. Пример. y=хsinx. Найти у```. Решение. y` = sinx + xcosx y`` = cosx + cosx – x sinx = 2cosx – x sinx y``` = -2sinx – sinx – x cosx = -3sinx – x cosx. Таблица неопределенных интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Пример 1. Вычислить Решение. Воспользуемся свойствами 4 и 5 неопределенных интегралов и первой табличной формулой. = 2(x2/2) – 3[(х3/2 *2)/3] – x + C = x2 - 2 Пример 2. = 2[(x1/2 *2)/1] – ln │x│ - 4 cosx +C = 4 Для вычисления неопределенных интегралов применяют следующие методы: метод непосредственного интегрирования, метод подстановки(метод замены переменной), метод интегрирования по частям. Существуют элементарные функции первообразные которых элементарными функциями не являются. По этой причине соответствующие неопределенные интегралы называются «неберущимися» в элементарных функциях, а сами функции не интегрируемыми в элементарных функциях. Например, Формула Ньютона - Лейбница. Понятие интегральной суммы. Пусть на отрезке [a, в] задана функция у = f(x). Разобьем отрезок на п элементарных отрезков точками деления а = х0, х1, х2, …, хп = в. На каждом элементарном отрезке [xi-1, xi] выберем произвольную точку Сi и положим
Эту сумму будем называть интегральной суммой для функции у=f(x) на отрезке [а, в]. Интегральная сумма зависит как от способа разбиения отрезка [a, в] на п частей так и от выбора точек С1, С2, …, Сп на каждом элементарном отрезке разбиения. Тесты к тема 2 1. Аксиома – составная часть дедуктивной системы. Это …? 1: Определение основных понятий данной науки. 2: Утверждение, требующее доказательства. 3: Утверждение, принимаемое без доказательств. 4: Некоторое логическое рассуждение. 2. Внутри дедуктивной системы не могут быть решены два вопроса. Какие из представленных? 1: Нужны ли доказательства аксиом? и Являются ли теоремы составной частью дедуктивного метода? 2: О смысле основных понятий. и Об истинности аксиом. 3:Можно ли определить в данной науке основные понятия? и Являюся ли доказательства составной частью дедуктивного метода? 3. Что представляет собой книга «Начала» Евклида? 1: Философское учение греческого философа и ученого Евклида. 2: Аксиоматическое построение геометрии. 3: Мифы Древней Греции. 4: Учение о параллельных прямых. 4 Кто из математиков почти одновременно с Н.И. Лобачевским подошел к созданию неевклидовой геометрии? 1: Гаусс, Бойяй 2: Лагранж, Ферма 3: Пуассон, Эйлер 4: Коши, Буняковский
5. В каком году был построен Императорский Казанский Университет? 1; 1804 2: 1800 3: 1850 4: 1900. Тесты к теме 3. 1 Что представляет собой мнимая единица? 1: корень кв. из -1, 2: –1 3: (i)^2 4: (-1)^2
2. Найти корни квадратного уравнения х*х-х+1=0 1: Х1=1/2; Х2=3/2 2: Корней нет 3: Х1,2=1/2+-3/2i 4: Х1=2, Х2=-1
3. Произвести действия: Если Z1=1-2i, Z2= -2+3i, Найти Z1+Z2. 1: Z=1-i 2: Z= -1+i 3: Z=2+3i 4: Z=1+2i
4. Произвести действия: Если Z1=1-2i, Z2= -2+3i, Найти Z1*Z2. 1:Z= 4 2: Z=-8+3i 3: Z= -2+6i 4: Z=4-i
5. Найти Z”, если Z=2-i. 1: Z= -2-i 2: Z= -2+i 3: Z= 2+i 4: Z= 2
6. Представить число Z = -3 в виде комплексного числа. Указать его вещественную и мнимую части. 1: Z=3-3i, Re Z=3, Im Z= -3 2: Z=-3+iо, Re Z=-3, Im Z=0 3: Z=3i, Re Z=-0, Im Z=3 4: Z=3*i*i Re Z=0, Im Z=3
7. Найти корни квадратного уравнения х^2+4=0 1: Х=2 2: Корней нет 3: Х1,2=+-2i 4: Х= -2
8. Дано комплексное число Z= -3+2i. Найти координаты точки на плоскости хоу ему соответсвующие. 1; (-3;2) 2: (3,2) 3: (3, -2) 4: (-3,0)
9. Выделить вещественную и мнимую части числа Z=1-3i/5-i. 1: Z=1/5-3i 2: Z=4/13 – 7/13i 3: Z=1/26-3i 4: Z=1-i Тесты к теме 4. 1. Даны точки М1(3,1); М2(2,3); М3(6,0); М4(-3,-1). Определить какая из точек лежит на прямой 2х-3у-3=0 1: М1(3,1); 2: М2(2,3); 3: М3(6,0); 4: М4(-3,-1). 2. Дана прямая х-3у+2=0, точка М(1,у) лежит на этой прямой. Найти ордин ату этой точки. 1: у=-1, 2: у=0, 3: у=1, 4: у=5. 3. Дана прямая х-3у+2=0, точка Р(х,2) лежит на этой прямой. Найти абциссу этой точки. 1: х=0, 2: х=4, 3: х=1, 4: х= -4. 4. Даны точки А(-3,2) и В(1,6). Найти расстояние между ними АВ. 1: АВ=2. 2: АВ=4, 3: АВ=8, 4: АВ=4 * корень кв. из 2, 5. Даны четыре пары, указать какие из них являются параллельными прямыми.
6. Даны уравнения линий 1) у^2=х, 2)у=х^2+1, 3)х-у=0, 4)х^2 +у^2=1 Найти среди них уравнение прямой. 1: у^2=х,- 2: х - у=0, 3: у=х^2+1 4: х^2+у^2=1 7. Дано уравнение прямой у-2х+1=0. Записать это уравнение, как уравнение прямой с угловым коэффициентом. Найти отрезок в, отсекаемый прямой от оси ординат. 1: в= -1 2: в=1 3: в=1/2 4: в=0 8. Дана точка М(-1,2). Найти уравнение прямой проходящей через эту точку параллельно прямой 2х - у+3=0 1: х=2у 2: 2х - у=0; 3: х+у - 2=0; 4: 2х - у+4=0; 9. Среди заданных четырех прямых определить две перпендикулярные прямые. 1) х+у-5=0, 2)у=+х+2, 3)3х-3у+1=0, 4)2х=у 1: х+у-5=0, у=+х+2 2: х+у-5=0, 2х=у 3: у=х+2, у=2х 4: у=х+2, 3х-3у+1=0. 10. Дана прямая х+у-5=0. Найти точку А пересечения этой прямой с осью ох. 1: А(1,1); 2: А(-5,0); 3: А(5,0); 4: А(0,5) Тесты к теме 5. 1. Написать уравнение окружности с центром в начале координат, радиусом равным 2. 1: х^2 + у^2 = 4 2: х^2 + у^2 = 2
3: (х – 2)^2 + (у – 2)^2 = 4 4: х^2 = 2 2. Х^2 + у^2 + 2х = 0. Дано уравнение окружности. Указать точку, лежащую на этой окружности: М1 (0, 0), М2 (1, 2), М3 (- 1, 3); М4 (0, 2). 1: М2(1, 2), 2: М1(0, 0), 3: М3(- 1, 3), 4: М4(0, 2), 3. Из четырех уравнений найти уравнение эллипса. 1) х/25 + у/16 = 1, 2) х^2/9 + у^2/4 = 1, 3) у^2 = 1 – х, 4) х^2 + у^2 = 9 1: нет уравнения эллипса 2: х/25 + у/16 = 1 3: х^2/9 + у^2/4 = 1 4: х^2 + у^2 = 9 4. Выделить уравнение гиперболы из четырех уравнений: 1) х/16 - у/9 = 1, 2) х^2 – у^2 = 1, 3) х^2 + у^2 = 1, 4) х^2 + 2у^2 = 1 1: х^2 + 2у^2 = 1 2: х/16 - у/9 = 1, 3: х^2 + у^2 = 1, 4: х^2 – у^2 = 1, 5. Написать уравнение эллипса, зная, что малая полуось в=3, расстояние между фокусами F1 F2= 8. 1: x^2/64+y^2/9=1 2: x^2/16+y^2/9=1 3: x^2/8+y^2/9=1 4: x^2/25+y^2/9=1 6. Написать уравнение эллипса, если большая полуось а=в, эксцентриситет Е=0,5. 1: x^2/6+y^2/2=1 2: x^2/6+y^2/9=1 3: x^2/36+y^2/27=1 4: x^2+y^2=1 7. х^2/18 – y^2/4,5=1 Дано уравнение гиперболы. Написать уравнение асимптот. 1: y=+-х 2: у=+-1/2х; 3: y=+-1/18 х 4: y=1/3х 8. На параболе у^2=6х найти точку с абциссой равной 6 1: М(0,6) 2: М(6,6) 3: М(6,0) 4: М1(6,6) и М2(6,-6) 9. Дана парабола у^2=6х. Найти координаты фокуса F. 1: F(3/2;0) 2: F(3,0) 3: F(0,6) 4: F (0,3) 10. Написать уравнение гиперболы, если а=9, в=4. 1: x/81 - y/4=1 2: x^2/9+y^2/4=1 3: x^2/81 - y^2/16=1 4: x^2 - y^2=9 Тесты к теме 6. 1. Вычислить определитель!2 3! !4 5! 1: -2, 2: 22, 3: 2, 4: 7, 2. Вычислить определитель!2 3! !4 5! 1:-5, 2: 10, 3: 1, 4: 0, 3. Справедливо ли равенство!2 8 10!!1 4 5! !1 3 -1! =2!1 3 –1!? !2 0!1!2 0 1! 1: Нет, 2: Да, 4. Дан определитель!1 5 3! Найти минор М21 к элементу а21 = 6. !6 1 0! !3 0 –1!. 1: М21= 0, 2: М21= -2, 3: М21= 1, 4: М21= 4, 5. Дан определитель!1 5 3! Найти алгеброическое дополнение А21 к !6 1 0! элементу а21 = 6. !3 0 –1!. 1: А21= 2, 2: А21= -2, 3: А21= 1, 4: А21= 4, 6. Если элементы второй строки определителя умножить на соответствующие алгебраические дополнения и произведения сложить, то получим: 1: отрицательное число, 2: ноль, 3: любое число, 4: величину определителя,
2х-3у=1. Имеет ли эта система единственное решение? 1: Да, 2: Нет.
4х-4у=4 1: система не имеет решения, 2: система имеет единственное решение, 3: система неопределенная,
х+у-z =2 3х-у-2z=3 Указать свободные члены: 1:(5, -1, -2); 2: (2, 1, 3); 3: (-3, 1, -1); 4: (1, 2, 3); 10. Может ли определитель иметь три строки и два столбца? 1: Да. 2: Нет, Тесты к теме 7. 1. Выберите правильное утверждение: 1) Матрица может иметь любое число строк и столбцов. 2) Матрица всегда имеет одинаковое число строк и столбцов. 3) Матрица не может состоять из одной строки. 4) Матрица не может состоять из одного столбца. Ответ: 1) Ответ: 2) Ответ: 3) Ответ: 4) 2. Может ли матрица состоять из одного элемента? 1: Да, 2: Нет, 3: Да, если это элемент не равен нулю. 3. Умножить матрицу А=(1, -1, 3, ½) на число (-2): 1: -7 2: (1, -1, 3, -1) 3: (-2, -1, 3, ½) 4: (-2, 2, -6, -1) 4. Можно ли сложить матрицы 2*2 и 3*3? 1: Нет 2: Да. 5. Можно ли перемножить матрицы соразмерности 2*3 и 3*4? 1: Нет. 2: Да. 6. Транспонирование матриц – это: 1) Перестановка местами двух столбцов. 2) изменение знака у всех элементов, 3) Перестановка местами двух строк, 4) перестановка местами строк и столбцов, Ответ: 1) Ответ: 2) Ответ: 3) Ответ: 4) 7. Если размерность исходной матрицы равна 6*7, то транспонированная матрица будет иметь размерность:
1: 6*6 2: 6*7 3: 7*6 4: 7*7 8. Единичная матрица – это: 1: Матрица, у которой все элементы равны 1. 2: Матрица, у которой элементы главной диагонали равны 1, а остальные нули 3: Матрица, определитель которой равен 1. 4: Матрица, содержащая только один элемент. 9. Если А=(1,3, -2), В= (-1) (0) (2), то А*В равно 1: -5 2: (-1 0 –4) 3: (-1)(0)(-4) 4: Перемножить нельзя Тесты к теме 8. 1. N – множество натуральных чисел. Какое из множеств является его подмножеством: А= {2, 4, 6, 8…}, В= (N2, N3, N4,…}; С= {1, 1/2, 1/3, 1/4, …}; Д= {1, 0, 1}? 1: В, 2: А, 3: С, 4: Д, 2. Найти пересечение множеств А= {1, 3, 5, 7, 9} и В= {2, 4, 6, 8}. Ответ: пустое множество, 1: {1} 2: {1,2,3,4,5,6,7,8} 3: {0} 3. Найти объединение множеств А и В, если А = {1,3,5,7,9}; B = {2,4,6,8}. 1: AUB = {0} 2: AUB = 0 3: АUB = {1, 2, 3, 4, 5, 6, 7, 8, 9} 4: AUB = {2,4,6,8} 4. Найти разность множеств А \ В, если А = {1,2,3,4}; B = {0,1,2}. 1: А\B = {3, 4} 2: A\B = {0,3,4} 3: A\B = {0,1,2} 4: A\B = {1,2,3} 5. Если /х/<2, то в виде двух неравенств его можно записать так: 1: -2<x<2 2: -2<=x<=2 3: 0<x<2 4: -2<x<0. 6. Если /х-1/<E, то E – окрестность точки 1 можно записать так: 1: -Е<x<Е 2: 1-Е<x<1+Е 3: 0<x<1+Е 4: -Е<x<0. 7. Если х принадлежит [-1, 3]. Какое из значений может принять х? 1: x<-1 2: -x= -3 3: x=0 4: x=4. 8. Если х не принадлежит (-2, 2). Какое из значений может принять х? 1: x= -1. 2: -x= 0 3: x=2 4: x= -4 9. Если –2<х<=0, то решением является: 1: (-2, 0) 2: (-2, 0] 3: (-2, 2) 4: [-2, 0]. 10. Найти пересечение множеств (-2, 2) и (-3, 1): 1: (-3, 2) 2: [0, 1] 3: (-2, 1) 4: [-2, 0]. Тесты к теме 9. «Функция. Классификация функций». 1. Найти область определения функции у = (х-2) / (х^2 – 9) 1: (0, 2) 2: (-00, -9) U (9, 00).- 3: (2, 3). 4: (-00, -3) U (-3,3) U (3,00). 2 Найти область определения функции у = (х-1)^1/2 1: (-00, 00). 2: (0, 00). 3: [1, 00). 4: x = 0 3. Найти область определения функции у = lg(2+х) 1: (-2, 00). 2: [2, 00). 3: (-00, 00). 4: x = 0 4. Найти значения функции у = х^2/ (х-1) в точке х = 0. 1: у = -1. 2: у = 0. 3: у = 00. 4: у = 2 5. Найти значения функции у = х^2/(х-1) в точке х = 1. 1: у = -1. 2: у = 1. 3: не существует. 4: у = 2 6. Найти значения функции у = х^2/(х-1) в точке х = (а^2) +1. 1: у = не существует. 2: у = ([а^2]+1)/а^2. 3: у = -1. 4: у = [(а^2 + 1)^2]/а^2. 7. Дана функция у = (sinх)^2 +5. К какому классу функций она принадлежит? 1: Трансцендентная. 2: алгебраическая. 8. Написать целую алгебраическую функцию второй степени, в общем виде. 1: у = х^2. 2: у = [(А0)*х^2] + (А1)*х + А2. 3: у = [(А0)х^2]+1. 4: у = (х^2)/(х+1) 9. Указать дробно-рациональную функцию из заданных функций: 1) у=2*х/(1+х+х^2); 2) у=х/(sinх); 3) у=(2)^х/2; 4) у= lg(х+2)/(х-2) Ответ: 1). Ответ: 2). Ответ: 3). Ответ: 4). 10. Дана сложная функция у = [sin (1-х)]^2. Представить ее в виде цепочки простых функций. 1: U = sin x, V = U-1, y = (U-1)^2. 2: U = sin(1-x), y = U^2. 3: U = 1-х, V = sinU, y = V^2. 4 y = [sin(1-x)]^2 – простая функция
Тесты к теме 10.
1: 2 2: 0 3: не существует. 4: 1
1: не существует. 2: 0 3: 2/3 4: 1/2
1: 0 2: 5/6 3: 1/2 4: 1/6
1: 1 2: 0 3: -1 4: 00
1: 1 2: 0 3: не существует. 4: 00
1: не существует. 2: 0 3: 00 4: 5
1: 00 2: 1 3: е 4: не существует
1: е2 2: е 3: 1 4: 00 9. Является ли функция у=х2 непрерывной в точке х=2 1: Нет 2: Да 10. Является ли функция у=1/(2х+1) непрерывной в точке х=1 1: Да 2: Нет Тесты к теме 11. 1. Найти приращение функции у=1/х, если х=1, ∆х=0,1. 1: - 1/11, 2: 0,1, 3: 0,01, 4: - 1, 2. Пользуясь определением производной, найти производную от функции у=х^3. 1: 3х^2∆х, 2: х^2, 3: 3х^2 - 1, 4: 3х^2, 3. Найти производную от функции у=хe^x, в точке х=0. 1: e+e^-1, 2: e^1, 3: 1, 4: 0, 4. Найти производную от функции у=х^5 – ¼x^4 + 3, в точке х. 1: 5x^4 – x^3 + 3, 2: 5х^4 – x^3, 3: 5x^4 – x^4 + 1, 4: 3, 5. Найти производную от функции у=sinx/cosx 1: sinx - cosx, 2:-cosx/sinx, 3: 1/cosx^2, 4: 1, 6. Найти дифференциал функции у=х^3 – 1. 1: 3(dx)^2, 2: 3x^2, 3: 3dx, 4: 3х^2dx, 7. Дана функция у=3х^2 – х + 1. Найти у`` 1: 6x, 2: 6, 3: 1, 4: 6x^2, 8. Найти у```, если у=х^6 – 1/4х^4+1/2x^2+2. 1: 120х^3 – 2x, 2: 120x^3, 3: 120x^3 – 2x +2, 4: 120, 9. Найти у```, если у=(х^2)*e^x. 1: 2e^х + 4xe^x +(x^2)*e^x, 2: 2xe^x+(x^2)*e^x, 3: 2xe^x + e^x, 4: 2e^x, Тесты к теме 12. 1. Найти первообразную для функции у = х. 1: х – 2 2: 2х, 3: 2х^2, 4: (х^2)/2. 2. Даны функции F1 (x) = sinx – 8, F2 = sinx +3. Первообразными для какой функции они являются? 1: х, 2: cosx, 3: -cosx, 4: -х. 3. Найти производную от функции $ln(x^2 +1)dx. 1: 2х/ [(x^2) +1], 2: ln[(х^2)+1]. 3: ln((х^2)+1)dx, 4: 1/((x^2)+1) 4. Найти дифференциал от функции $x arcsin2x dx. 1: x arcsin2x dx. 2: arcsin2х, 3: arcsin2x dx, 4: [arcsin2x +2x/ (1-4(x^2))^1/2]dx. 5. Вычислить $d(2^x^2) 1: (2^х^2) (ln2)2x, 2: (2^х^2)+C. 3: (2^х^2)dx, 6. Вычислить интеграл $(x^2 -3)dx. 1: [(x^3)/3x] – 3x, 2: [(х^3)/3] – 3х +С. 3: (3х^3)+C, 4: [(x^2)-3]+C 7. Справедлива ли формула $U(x) V(x)dx = $U(x)dx*$V(x)dx? 1: Нет 2: Да. 8. Можно ли вынести постоянный множитель за знак интеграла? 1: Да. 2: Нет 9. Указать какие из интегралов является «неберущимися» $sin(x^2) dx, $lnx/x dx, $[1+ (x^1/3)] dx. 1: sin(x^2) dx. 2: $ lnx/x dх, 3: $[1+x^1/3]dx. 10. Указать какие из интегралов является «неберущимися» $(e)^-x^2 dx, $xe^x^2, $x^2 e^-x^2 dx, $xe^-x^2 dx. 1.$xe^-x^2 dx, 2: $ xe^x^2 dх, 3: $e^-x^2 dx 4: $[(x^2) (e^-x^2)] dx. Тесты к теме 13. 1. Вычислить интеграл в пределах (1, 00) от функции dx/(x^2). 1: 1, 2: расходится, 3: 0, 4: -1, 2. Вычислить интеграл в пределах (0, 00) от функции e^-x dx. 1: расходится, 2: 1, 3: 0, 4: -1, 3. Вычислить интеграл в пределах (-00, 00) от функции e^-2x dx. 1: -1, 2: 0, 3: 1, 4: расходится, 4. Вычислить интеграл в пределах (0, 1) от функции dx/x. 1: 2, 2: сходится 3: расходится, 4: 0, Тесты к теме 14. 1. Зависит ли интегральная сумма для функции у=f(x) на отрезке [а, в] от способа разбиения отрезка на 10 частей? 1: Да, 2: Нет, 2. Зависит ли интегральная сумма для функции у=f(х) на отрезке [а, в]от выбора точек Сi на i элементарном отрезке, i = 1,2,…,п?. 1: Нет, 2: Да, 3. Можно ли записать интеграл в пределах (0, 2) от функции (sinx^2 – 3x^1/2)dx = $ в пределах от (0, 2) от функции sinx^2 dx + 3$ в пределах (0, 2) от функции х^1/2 dx? 1: Да, 2: Нет, 4. Можно ли записать интеграл в пределах (0, 2) от функции f(x)dx = интегралу в пределах (0, 1) от функции f(x)dx + интеграл в пределах (1, 2) от функции f(x)dx. 1: Нет, 2: Да, 5. Вычислить интеграл в пределах (4, 3) от функции (x^1/2)dx. 1: 2/3, 2: 19, 3: 38/3, 4: 1, 6. Вычислить интеграл в пределах (0,П/2) от функции (sinx)dx. 1: 1/2, 2: -1, 3: 0, 4: 1, 7. Вычислить интеграл в пределах (1, 3) от функции dx/х^2. 1: -1/3, 2: 2/3, 3: 1, 4: 0, 8. Найти значение интегральной суммы для f(x) = 1 на отрезке [a, в]. 1: в-а, 2: ав, 3: 1/в-а, 4: 2, 9. Верно ли равенство интеграл в пределах (0, 2) от f(x)dx.= - интеграл в пределах (2, 0) от f(x)dx? 1: Нет. 2: Да,
.
МАТЕМАТИКА
Тема 11. Производная и дифференциал. Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица неопределенных интегралов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.76.84 (0.011 с.) |



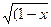 2)
2)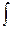 хα dx = [xα+1 / (α +1)] +C, α ≠ -1, α Є R
хα dx = [xα+1 / (α +1)] +C, α ≠ -1, α Є R 2-x2) = (arcsin x/a) + C
2-x2) = (arcsin x/a) + C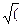 a2 +x2) = ln │x+
a2 +x2) = ln │x+  -1)dx.
-1)dx. 7. Дана система уравнений х+у=3
7. Дана система уравнений х+у=3 8. Дана система уравнений х - у=1
8. Дана система уравнений х - у=1 9. Дана система 2х-3у+5z=1
9. Дана система 2х-3у+5z=1


