Производная функции и ее геометрический смысл.

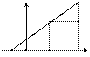
Приращением функции y =f(x) в точке x₀ называется разность

Δу=f(x)-f(x₀)= f(x+Δx)-f(x0)

Производной от функции y=f(x) в точке х0 наз. Предел отношения Δу/Δх, когда Δх→0 (при усл., что этот предел существует)

Написать обозначение производной.

Геометрический смысл производной.

Пусть Г- график функции y=f(x). Рассмотрим на Г т. А(x0,f(x0)) и т. В (x0+Δx,f(x0+Δx))

В

С

y=f(x) А

 

 

Прямая АВ называется секущей. Будем считать, что y=f(x)-непрерывная функция, тогда если Δх→0, то f(x0+Δx)→f(x0), т.е. В→А при Δх→0.

Пусть γ – угол наклона секущей относительно оси ОХ. Если существует предел lim γ=γ0 при Δх→0, то прямая, проходящая через А и образующая с осью ОХ угол γ0, называется касательной к Г в точке А.

Пусть С(f(x0+Δх), f(x0)) – точка, дополняющая отрезок АВ до прямоуг. треугольника АВС. Т.к. АС//ОХ, то tgγ =Δу/Δх. Переходя к пределу, получим: tgγ0=f′(x0)

Т.е. геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x₀))_.

Уравнение касательной.

Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т. А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0, значит, касательная задается след. Ур-м:

y= kx+ f(x0)-kx0= f(x0)+k(х-x0)

Т.к. k= f′(x0), то

y=f(x0)+ f′(x0)(х-х0).

Односторонние производные.

Правой(левой) производной от y=f(x) в точке x₀ называется предел f′(x0)=lim (f(x+Δx)-f(x0))/Δх при Δх→0+0(Δх→0-0).

Если левая и правая производные функции в точке x₀ сущ-т, и они равны, то производная f′(x0) сущ-т и равна им. Если же левая и правая производные функции в точке x₀ не равны, то y=f(x) не имеет производной в точке x_0.

Правила дифференцирования

Теорема. Если функции u=f(x), v=g(x) дифференцируемы в точке х0, то сумма, разность, произведение и частное этих функций также дифференцируемы в точке ч0 и выполняются следующие формулы:

(U+(-)v)′=u’+(-)v’

(uv)’= u’v + uv’

(u/v)’= (u’v - uv’)/v²

Производная сложной и обратной функций.

Теорема. Если функция y=f(x) дифференцируема в точке t0, g(t0)=x0, то сложная функция y=f(g(x)) также дифференцируема в точке t0 и выполняется след. Формула:

f’(g(x))=f’(x0)*g’(t0)

Теорема. Если y=f(x) имеет обратную ф-ю x=g(y) и в точке х0 производная f′(x) не равна 0, то обратная функция g(y) диф-ма в точке y0=f(x0) и

g’(y)=1/f(x0)

 

Производная элементарных функций.

Обл. определения производной f’(x) явл. множество всех точек x₀, в которых y=f(x) имеет конечную производную.

Производная каждой элементарной ф-и явл. элементарной ф-ей.

Производная логарифмической ф-и: (log_ax)’=1/xlna

Производная показательной ф-и: a^x= a^x lna

Производная степенной ф-и: ( x^a)’ = ax^a-1

Производная тригонометрической функции:

(Sinx)’=cosx

(cosx)’=-sinx

(tgx)’=1/cos²x

Производные обратных тригонометрических функций:

(Arcsinx)’=1/(1-x²)^1/2

(Arccosx)’=-1/(1-x²)^1/2

(arctgx)’=1/(1+ x²)

 

Понятие функции, дифференцируемой в точке.

Опр. Функция у= f (x) называется дифференцируемой в точке х₀, если ее приращение в х₀ можно представить в виде ∆у=А∆х+α(∆х)∆х (*), где А – некоторое число, α(∆х) – функция от ∆х, являющаяся бесконечно малой при ∆х→0. Связь между дифференцируемостью функции в точке и существованием производной в этой же точке устанавливает Теорема.

Теорема. Для того чтобы f (x) была дифференцируема в точке х_0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. 1. Необходимость. Пусть функция у= f (x) дифференцируема в х_0. Тогда ее приращение можно представить в виде (*). Следовательно

 

 

Следовательно производная существует и равна А. 2. Достаточность. пусть существует конечная производная f ′ (х₀)=А. Тогда по определению производной, lim_∆х→0(∆у/∆х)=А. положим, что α(0)=0 и α(∆х)= (∆у/∆х) – А, если ∆х≠0. Определеннная так функция α(∆х) является бесконечно малой при ∆х→0. Действительно lim_∆х→0α (∆х)= lim_∆х→0((∆у/∆х) – А)=А – А=0. Кроме того, ∆у=А∆х+α(∆х)∆х. Тем самым доказано, что функция дифференцируема в х_0.

Замечание. Если функция дифференцируема в х₀, то из (*) следует, что ∆у→0, когда ∆х→0, т.е. функция непрерывна в данной точке. Обратное утверждение неверно. Функция может быть непрерывной, но не дифференцируемой в данной точке.

Пусть f (x) дифференцируема в х₀,следовательно, существует производная и коэффициент А из (*) совпадает с производной, как следует из доказательства теоремы. Тогда формулу (*) можно представить

f (x)=f(х₀)+ f ′ (х₀) ∆х +α(∆х)∆х. α(∆х) б.м. функция (∆х→0)

(**)

∆f(х₀)~ f ′ (х₀) ∆х (приращение функции эквивалентно произведению производной на приращение аргумента)