Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые и бесконечно большие функции.Содержание книги
Поиск на нашем сайте
Опр. Функция f (x) наз.бесконечно малой при х →х0, если
Справедливы теоремы. 1.Сумма и произведение двух бесконечно малых функций (при х →х0) снова являются бесконечно малыми функциями (при х →х0). Произведение бесконечно малой функции на ограниченную есть снова бесконечно малая функция. Свойства предела функции. 1. Функция f (x) в точке х0 может иметь только один предел. Доказательство: Пусть (1) и одновременно где a≠b. (2)
Тогда для любой последовательности { хn} сходящейся к х0 (где все хn≠ х0), мы должны иметь два предела
что невозможно, т.к. последовательность { f (хn)} может иметь только один предел. 2.Если f (x) имеет предел в точке, то в некоторой окрестности этой точки функция ограничена. Доказательство. Предположим, что это не так. U1=(х0-ε; х0+ε), ε>0. Ввиду неограниченности f (x) в этой окрестности должна найтись точка х1Î U1, такая что │ f (х1)│>1. Уменьшим вдвое эту окрестность и рассмотрим U2=(х0-ε/2; х0+ε/2), ε>0 окрестность, в ней снова найдется такая точка х2Î U2, такая что │ f (х2)│>2. Продолжив это рассуждение, получим Un=(х0-ε/n; х0+ε/n), f (хn) > n, хn → х0; f (хn)→∞. мы пришли к противоречию. 3.Если для всех точек х некоторой окрестности точки х0 выполняется неравенство f (x) ≥b, то и если такой предел существует. (доказывается по соответствующему свойству предела числовой последовательности).
Арифметические свойства пределов.
Односторонние пределы.
Аналогично определяют предел функции слева: Асимптоты функций. Прямая у=а называется вертикальной асимптотой графика у= f (x), если хотя бы один из пределов
Теорема. Для того чтобы график функции у= f (x) имел х→+∞ наклонную асимптоту, необходимо и достаточно, чтобы существовали два предела Аналогично определяется наклонная асимптота для случая х→-∞.
Монотонные функции. Функция y=f(x) называется возрастающей (убывающей) на некотором множестве Х принадл. R1, если она определена на этом множестве и если для любых значений х1, х2, принадлежащим Х, из условия х1<х2 следует нер-во: f(x1)<f(x2) (f(x1) >f(x2)) Функция y=f(x) называется неубывающей (невозрастающей) на некотором множестве Х принадл. R1, если она определена на этом множестве и если для любых значений х1, х2 принадлежащим Х из условия х1<х2 следует нер-во: f(x1)≤f(x2) (f(x1) ≥f(x2)) Невозрастающие, неубывающие, возрастающие и убывающие ф-и наз. Монотонными. Любая ограниченная монотонная функция имеет предел. Замечательные пределы. 1) lim f(x)sinx/x =1(при х→0) – первый замечательный предел. Док-во. Т.к. ф-я y= sinx – четная, то достаточно показать, что предел при х→0 справа равен 1.
T M tgx
x K A O MK= sinx Видно, что sinx<x<tgx, 1<x/ sinx<1/cosx 1>sinx/x>cosx при х→0 справа имеем lim cosx=1, lim 1=1. Значит получили требуемое равенство. 2) lim (1+1/x)x =e(х→+ (-)∞) – второй замечательный предел. Док-во. Докажем 1)при +∞. Пусть х – любое число. Найдем такое целое n, чтобы выполнялось нер-во: n ≤ x< n+1 (1) Будем считать, что х>1,n>0. Сделав необходимые преобразования, получим: 1+1/ n ≥ 1+1/x> 1+1/(n+1) Зная условие (1), можем получить: (1+1/ n)n+1≥ (1+1/x)x> (1+1/(n+1))n или f(x) ≥(1+1/x)x>g(x). При х→+∞,n →+∞, f(x) и g(x)→е. По св- ву предела ф-и lim (1+1/x)x →е(при х→+∞), что и т.д. 2) при -∞. Пу сть х=-t, где t>0. (1+1/x)x=(1-1/t)-t =((t-1)/t)-t =(t/(t-1))t =(1+1/(t-1))t =(1+1/(t-1))t-1 (1+1/(t-1))x Выражение в правой части →е*1=е при х→-∞, т.е. t →+∞, что и т.д. Формула непрерывных процентов. К0-исходный капитал. Р- номинальная процентная ставка. к- число периодов начисления. Пусть к=1, тогда К=К0*(1+р/100) к=2, К=К0(1+р/2*100)2 … к=360, К=К0(1+р/360*100)360 …,т.е. К=К0(1+р/к*100)к→К0*ер/100 при к →∞(это случай, если начисление процентов производится в течение одного года). Когда начисление процентов производится на протяжении нескольких лет – t, то, разделив промежуток [0;t] на к равных периодов начисления процентов, получим (к→∞): К0lim (1+рt/100*к)к= К0*ерt/100 К=К0*ерt/100 -формула непрерывных процентов.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.128.171 (0.008 с.) |




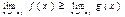 4.Если в некоторой окрестности точки х0 имеем f (x)≥g(x), то и если пределы существуют.
4.Если в некоторой окрестности точки х0 имеем f (x)≥g(x), то и если пределы существуют. 5. Если в некоторой окрестности точки х0 имеем f (x)≥g(x)≥h(x) причем пределы f (x) и h(x) при х→ х0 существуют и равны между собой
5. Если в некоторой окрестности точки х0 имеем f (x)≥g(x)≥h(x) причем пределы f (x) и h(x) при х→ х0 существуют и равны между собой





 Опр.Число а называют пределом функции f (x)в точке х0 справа, если для любой сходящейся к х0 последовательности {хn}, в которой все хn>х0, соответствующая последовательность {f(хn)} сходится к а.
Опр.Число а называют пределом функции f (x)в точке х0 справа, если для любой сходящейся к х0 последовательности {хn}, в которой все хn>х0, соответствующая последовательность {f(хn)} сходится к а.

 Прямая у=кх+b является наклонной асимптотой графика у= f (x) при х→+∞, если f (x) представима в виде f (x)= кх+b+α(х), где
Прямая у=кх+b является наклонной асимптотой графика у= f (x) при х→+∞, если f (x) представима в виде f (x)= кх+b+α(х), где