
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные элементарные функции.Содержание книги
Поиск на нашем сайте
Функция, ОДЗ Пусть заданы 2 множества Х,У функцией или отображением из Х в У называется правило, по которому каждому значению их Х ставится в соотвествие значение из У. Числовые функции характеризуются тем, что оба множества Х и У являются подмножествами множества действительных чисел (или совпадают с ними). Область определения функции - множество возможных значений, которые может принимать аргумент. Графиком функции с областью определения называется множетсво точек Г={(x,f(x)|xÎX}. Свойства функции. 1. Чётность. Если облать определения функции симметричня относительно нуля и f(-x)=f(x) "xÎD(f), то функция у=f(x) называется чётной. Если f(-x)= - f(x) "xÎD(f), то функция у=f(x) называется нечётной. Если не выполняется ни первое, ни второе условие, то функция обшего вида. 2. Монотонность. функция у=f(x) – возрастающая, если для любого х1 и х2 из области определения функции (х1<х2) выполняется неравенство f(x1)<f(x2) Функция у=f(x) – убывающая, если для любого х1 и х2 из области определения функции (х1>х2) выполняется неравенство f(x1)>f(x2). Возрастающие или убывающие функции называются монотонными. 3. Ограниченность. Функция у=f(x) называется ограниченной на некотором промежутке, если существует М>0, MÎR|"xÎданному промежутку |f(x)|£M. Функция у=f(x) называется ограниченной снизу, если существует mÎR |"xÎданному промежутку m£f(x). Функция у=f(x) называется ограниченной сверху, если существует mÎR |"xÎданному промежутку m³f(x). 4. Периодичность. Функция у=f(x) называется периодической с периодом Т не равным нулю, если выволняется условие f(x+ - T)=f(x).
Обратная функция. Пусть Функция у=f(x) задана на множестве Х=D(f) и Y=E(f). Предположим, что различным значениям х1 и х2 соответствуют различные значения функции f(x1) и f(x2). Тогда для любого уÎУ мы сможем поставить в соответсвие хÎХ| y=f(x). Получает отображение f-1: У®Х. Это отображение называется обратным. График прямой и обратной функции симметричен относительно биссектрисы первой и третьей координатной четверти. Сложная функция. Пусть заданы две функции t=h(x), [xÎD(h), T=E(h)] и y=g(t), [tÎT=D(g), Y=E(g)] (область определения одной функции совпадает с областью значений другой функции и наоборот) Тогда справедливо следующее правило: из любого хÎХ по правилу ставится в соответствие y=g(h(x)). Это правило называется сложной функцией.
Основные элементарные функции. 1. Степенная. y=xa, a=const, aÎR. D(f)=(0;+¥). Если aÎNÞD(f)=R.
3. Логарифмическая. y=logax, a>0, a не равно 1. D(f)=(0;+¥), E(f)=R. Если a>1, следовательно, функция возрастает. Если аÎ(0;1), функция убывает. 4. Тригонометрические. 5. Обратные тригонометрические.
Предел функции Опр. Пределом функции у= f (x) в точке х0 (или при х →х0)называют число а, если для любой последовательности { хn} значений аргумента, сходящейся к (при этом все хn≠ х0) последовательность значений функции сходится к пределу а. Это записывают в виде:
(*) Аналогично определяеся предел при х →∞ (случаи когда х0 есть +∞ или -∞). А именно, равенство (*) во всех случаях означает следующее: для любой последовательности { хn}, сходящейся к х0, соответствующая последовательность { f (хn)} сходится к а.
Бесконечно малые и бесконечно большие функции. Опр. Функция f (x) наз.бесконечно малой при х →х0, если
Справедливы теоремы. 1.Сумма и произведение двух бесконечно малых функций (при х →х0) снова являются бесконечно малыми функциями (при х →х0). Произведение бесконечно малой функции на ограниченную есть снова бесконечно малая функция. Свойства предела функции. 1. Функция f (x) в точке х0 может иметь только один предел. Доказательство: Пусть (1) и одновременно где a≠b. (2)
Тогда для любой последовательности { хn} сходящейся к х0 (где все хn≠ х0), мы должны иметь два предела
что невозможно, т.к. последовательность { f (хn)} может иметь только один предел. 2.Если f (x) имеет предел в точке, то в некоторой окрестности этой точки функция ограничена. Доказательство. Предположим, что это не так. U1=(х0-ε; х0+ε), ε>0. Ввиду неограниченности f (x) в этой окрестности должна найтись точка х1Î U1, такая что │ f (х1)│>1. Уменьшим вдвое эту окрестность и рассмотрим U2=(х0-ε/2; х0+ε/2), ε>0 окрестность, в ней снова найдется такая точка х2Î U2, такая что │ f (х2)│>2. Продолжив это рассуждение, получим Un=(х0-ε/n; х0+ε/n), f (хn) > n, хn → х0; f (хn)→∞. мы пришли к противоречию.
3.Если для всех точек х некоторой окрестности точки х0 выполняется неравенство f (x) ≥b, то и если такой предел существует. (доказывается по соответствующему свойству предела числовой последовательности).
Односторонние пределы.
Аналогично определяют предел функции слева: Асимптоты функций. Прямая у=а называется вертикальной асимптотой графика у= f (x), если хотя бы один из пределов
Теорема. Для того чтобы график функции у= f (x) имел х→+∞ наклонную асимптоту, необходимо и достаточно, чтобы существовали два предела Аналогично определяется наклонная асимптота для случая х→-∞.
Монотонные функции. Функция y=f(x) называется возрастающей (убывающей) на некотором множестве Х принадл. R1, если она определена на этом множестве и если для любых значений х1, х2, принадлежащим Х, из условия х1<х2 следует нер-во: f(x1)<f(x2) (f(x1) >f(x2)) Функция y=f(x) называется неубывающей (невозрастающей) на некотором множестве Х принадл. R1, если она определена на этом множестве и если для любых значений х1, х2 принадлежащим Х из условия х1<х2 следует нер-во: f(x1)≤f(x2) (f(x1) ≥f(x2)) Невозрастающие, неубывающие, возрастающие и убывающие ф-и наз. Монотонными. Замечательные пределы. 1) lim f(x)sinx/x =1(при х→0) – первый замечательный предел. Док-во. Т.к. ф-я y= sinx – четная, то достаточно показать, что предел при х→0 справа равен 1.
T M tgx
x K A O MK= sinx Видно, что sinx<x<tgx, 1<x/ sinx<1/cosx 1>sinx/x>cosx при х→0 справа имеем lim cosx=1, lim 1=1. Значит получили требуемое равенство. 2) lim (1+1/x)x =e(х→+ (-)∞) – второй замечательный предел. Док-во. Докажем 1)при +∞. Пусть х – любое число. Найдем такое целое n, чтобы выполнялось нер-во: n ≤ x< n+1 (1) Будем считать, что х>1,n>0. Сделав необходимые преобразования, получим: 1+1/ n ≥ 1+1/x> 1+1/(n+1) Зная условие (1), можем получить: (1+1/ n)n+1≥ (1+1/x)x> (1+1/(n+1))n или f(x) ≥(1+1/x)x>g(x). При х→+∞,n →+∞, f(x) и g(x)→е. По св- ву предела ф-и lim (1+1/x)x →е(при х→+∞), что и т.д. 2) при -∞. Пу сть х=-t, где t>0. (1+1/x)x=(1-1/t)-t =((t-1)/t)-t =(t/(t-1))t =(1+1/(t-1))t =(1+1/(t-1))t-1 (1+1/(t-1))x Выражение в правой части →е*1=е при х→-∞, т.е. t →+∞, что и т.д. Уравнение касательной. Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т. А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0, значит, касательная задается след. Ур-м: y= kx+ f(x0)-kx0= f(x0)+k(х-x0) Т.к. k= f′(x0), то y=f(x0)+ f′(x0)(х-х0). Односторонние производные. Правой(левой) производной от y=f(x) в точке x0 называется предел f′(x0)=lim (f(x+Δx)-f(x0))/Δх при Δх→0+0(Δх→0-0). Если левая и правая производные функции в точке x0 сущ-т, и они равны, то производная f′(x0) сущ-т и равна им. Если же левая и правая производные функции в точке x0 не равны, то y=f(x) не имеет производной в точке x0.
Правила дифференцирования Теорема. Если функции u=f(x), v=g(x) дифференцируемы в точке х0, то сумма, разность, произведение и частное этих функций также дифференцируемы в точке ч0 и выполняются следующие формулы: (U+(-)v)′=u’+(-)v’ (uv)’= u’v + uv’ (u/v)’= (u’v - uv’)/v2 Приближенные вычисления. D f (x0)»f '(x0) Dx f (x0+Dx)- f (x0)» f '(x0) Dx Dx®0 f (x0+Dx)= f (x0)+ f '(x0) Dx
Формула Тейлора. Пусть функция f(x) имеет n производных в точке x0. Многочлен T(x) = f(x0) + ((f’(x0))/1!)(x – x0)1 + (f ”(x0))/2!(x – x0)2 +…+ (f (n)(x0))/n!(x – x0)n Называется n-м многочленом Тейлора функции f(x) в точке x0. Пусть функция f(x) имеет в ε – окрестности точки x0 (n + 1) производных. Тогда для любой точки х из этой окрестности найдется точка с, расположенная между точками х и х0, для которой выполняется следующая формула F(x) = T(x) + (f(n+1)(c) / (n + 1)!)(x – x0)n+1 – формула Тейлора, где Т(x) – n-й многочлен Тейлора функции f(x) в точке х0, rn(x) = (f(n+1)(c) / (n + 1)!)(x – x0)n+1 – остаточный член в формуле Лагранжа. Предположим, что (n+1)-я производная функция f(x) ограничена в окрестности точки х0. Тогда rn(x) является бесконечно малой более высокого порядка, чем (х-х0)n при х ® х0. (lim (rn(x)/(х-х0)n) = lim [((f(n+1)(c))/(n+1)!)(x-x0)] = 0 – в силу Х®Хо Х®Хо Ограниченности f(n+1) (c) в окрестности х0.) Следовательно ошибка в приближенном равенстве f(x)» Tn(x) (*) также является бесконечно малой более высокого порядка, чем (х – х0)n, когда х ® х0. Формула (*) применяется для приближенных вычислений. Используя равенство (*) можно подучить, например следующие формулы (при х®0): 1) (1+x)a» 1 + (a/1!)x + (a(a-1)/2!)x2 +…+ (a(a-1)…(a-n+1)/n!)xn, 2) ex» 1 + x/1! + x2/2! +…+ xn/n!, 3) ln(1+x)» x – x2/2 + x3/3 – x4/4 +…+(-1)n+1xn/n 4) sin x» x – x3/3! + x5/5! – x7/7! +…+(-1)kx2k+1/(2k+1)!, 5) cos x» 1 – x2/2! + x4/4! – x6/6! +…+(-1)kx2k/(2k)!, где в каждом случае ошибка является бесконечно малой относительно хn.
Условия сущ. экстремула Необходимое условие существования экстремума. Для того, чтобы дифференцируемая функция f(x) имела в точке х0 локальный экстремум, необходимо, чтобы в этой точке выполнялось равенство f¢(x0)=0. Доказательство. Поскольку х0 – точка экстремума, то существует такой интервал (х0-e, х0+e), на котором f(x0) – наибольшее или наименьшее значение. Тогда по теореме Ферма f¢(x0)=0. Точки, в которых производная функция обращается в нуль, называются стационарными. Достаточное условие существование экстремума. Если при переходе через точку х0 производная дифференцируемой функции f(x) меняет свой знак с плюса на минус, то точка х0 – точка локального максимума функции f(x), а если с минуса на плюс, то х0 – точка локального минимума.
Доказательство. (для максимума, для минимума – аналогично, то бишь самостоятельно) Пусть f(x) – непрерывная дифференцируемая функция. f¢(x) меняет знак с «+» на «-». Пусть для любого хÎ (х0 -D, х0] f¢(x)>0 Þ по достаточному условию монотонности производная возрастает на данном интервале Þ f(x0)³f(x) "CÎ(x0-D, x0] Пусть для "CÎ[х0,х0+D) f¢(x)<0, следовательно, функция убывает на хÎ[х0,х0+D) Þf(x0)³f(x) для любого хÎ[х0,х0+D). Вывод: для любого х Î (х0-D, х0+D) х0 – точка максимума для функции у=f(x). Ч.т.д. Теорема Ферма Пусть ф-я у = f(x) определена в некотором промежутке [a;b] и во внутренней точке этого промежутка спринимает наибольшее или наименьшее значение. Если в этой точке существует конечная производная, то она = 0. С ¹ a, с ¹ b, f(c) – max. Докажем, что f'(c) = 0. Т.к. f(c) - max, то для всех точек f(x) £ f(c) при xÎ[a;b] f(x) - f(c) £ 0 Т.к. по условию теоремы в точке с ф-я f имеет производную, то можно рассмотреть производную f'(c) = lim (f(x)-f(c))/(x-c) 1) x-c < 0 f’(c)³ 0ü Þ f’(c) = 0 2) x-c > 0 f’(c)£ 0þ Теорема Ролля Эта теорема позволяет отыскать критические точки, а затем с помощью достаточных условий исследовать ф-ю на экстремумы. Пусть 1) ф-я f(x) определена и непрерывна на некотором замкнутом промежутке [a;b]; 2) существует конечная производная, по крайней мере, в открытом промежутке (a;b); 3) на концах промежутка ф-я принимает равные значения f(a) = f(b). Тогда между точками a и b найдется такая точка с, что производная в этой точке будет = 0. Док-во: По теореме о свойстве ф-ий, непрерывных на отрезке, ф-я f(x) принимает на этом отрезке свое max и min значение. f(x1) = M – max, f(x2) = m – min; x1;x2 Î [a;b] 1) Пусть M = m, т.е. m £ f(x) £ M Þ ф-я f(x) будет принимать на интервале от a до b постоянные значения, а Þ ее производная будет равна нулю. f’(x)=0 2) Пусть M>m Т.к. по условиям теоремы f(a) = f(b) Þ свое наименьшее или наибольшее значение ф-я будет принимать не на концах отрезка, а Þ будет принимать M или m во внутренней точке этого отрезка. Тогда по теореме Ферма f’(c)=0. Теорема Лагранжа Пусть 1) ф-я f(x) определена и непрерывна на интервале [a;b] 2) Существует конечная производная, по крайней мере, в открытом интервале (a;b). Тогда между a и b найдется такая точка с, что для нее выполняется следующее равенство: (f(b)-f(a))/(b-a)=f’(c), a < c< b Док-во: Введем вспомогательную ф-ю F(x). F(x) = f(x) - f(a) - [(f(b)-f(a))/(b-a)]*(x-a) Эта ф-я удовлетворяет всем условиям теоремы Ролля: 1) она непрерывна как разность между непрерывной и линейной функциями; 2) в открытом интервале (a;b) существует конечная производная этой ф-ии. F’(x) = f’(x) - (f(b)-f(a))/(b-a) 3) на концах промежутка в точках a и b эта ф-я равна 0 F(a) = f(a) - f(a) - (f(b)-f(a))/(b-a)*(а - а) = 0 F(b) = f(b) - f(a) - (f(b)-f(a))/(b-a)*(b-a) = 0 Þ производная в какой-либо внутренней точке с равна 0. F’(с) = 0 f’(c) - (f(b)-f(a))/(b-a) = 0, отсюда f’(c) = (f(b)-f(a))/(b-a) Геометрическое истолкование CB/AC = (f(b)-f(a))/(b-a) На дуге АВ найдется по крайней мере одна точка М, в которой касательная || хорде АВ. Первообразная. Ф-я F(x) называется первообразной ф-и f(x) на множестве D, если для любого х из D:F’(x)=f(x). Если F(x) первообрзная ф-и f(x) на мн-ве D, то любую другую первообразную этой ф-и можно получить по формуле: Ф(х)=F(x)+c при некотором значение с.
Док-во. Пусть F(x) – первообразная f(x), x принадлежит D: F’(x)=f(x). Пусть Ф(х) – другая первообразная f(x), x принадл. D: Ф’(x)=f(x). Составим ф-ю φ(х)=Ф(х)-F(х) – дифференцируема на мн-ве D → φ'(х)= Ф’(х)-F’(х)=f(x)-f(x)=0. По св-м ф-и, дифференцируемой на D → φ(х)=соnst.=c → Ф(х)-F(х)=с=const → Ф(х)=F(х)+с, что и т.д. Табличные интегралы. Таблица интегралов 1) ∫ 0 dx = C = const 11) ∫dx/(√1-x2 )= arcsin x + C = - arccos x + C 2) ∫dx = x + C 12) ∫dx/(1+x2) = arctg x + C = - arcctg x + C 3) ∫xadx = xa+1/(a+1) + C, 13) ∫tgxdx = - ln |cosx| + C a≠ -1 14) ∫ctgxdx = ln |sinx| + C 4) ∫dx/x = ln|x| + C 15) ∫ dx/(√a2- x2)=arcsinx/a +C=-arccos x/a + C 5) ∫exdx = ex + C 16) ∫dx/(a2+x2) = (1/a)arctg x/a + C=-(1/a)arcctg x/a + C 6) ∫axdx = ax/lnx + C 17) ∫dx/(x2–a2) = (1/2a) ln |(x-a)/(x+a)| + C 7) ∫cosx dx = sinx + C 18) ∫dx/(a2-x2) = (1/2a) ln |(x+a)/(x-a)| + C 8) ∫sinxdx = - cosx + C 19) ∫dx/(√x2+A) = ln |x + (√x2+A)| + C 9) ∫dx/cos2x = tgx + C 20) ∫(√x2+A)dx = (x/2)(√x2+A) + (A/2) ln |x+(√x2+A)|+C 10) ∫dx/sin2x = - ctgx + C 21) ∫ (√a2- x2)dx = (a2/2) arcsin x/a + (x/2) (√a2- x2) + C Неявные функции Пусть переменная u, является функцией переменных х1, х2,…, хn, задается посредством функционального уравнения F (х1, х2,…, хn, u) = 0. В этом случае говорят, что u как функция аргументов х1, х2,…, хn задана неявно, а саму функцию u называют неявной функцией. Неявные функции могут задаваться и посредством системы функциональных уравнений. Производная функции y = y(x), заданной неявно уравнением F(x,y) = 0, где F(x, y) – диффиренцируемая функция переменных x и y, может быть вычислена по формуле: y’ = - F’x / F’y При условии, что F’y ≠ 0. Аналогично частные производные неявной функции двух переменных u = (х1, х2), заданной с помощью уравнения F(х1, х2, u) = 0, где F(х1, х2, u) – дифференцируемая функция переменных х1, х2, u могут быть вычислены по формулам: ∂u / ∂x1 = - F’x1 / F’u, ∂u / ∂x2 = - F’x2 / F’u. Метод наименьших квадратов. (рассмотрим для двух величин, остальные аналогично0Пусть (Х,У) – система двух случайных величин. Задача – исследовать связь между Х и У. М(У/Х=х) – условные математические ожидания случайной величины У при условии, что Х=х (х – фиксированное число) М(У/Х=х)=f(x). Уравнение y=f(x) называется уравнением регрессии СВ У на СВ Ч. Будем приближать функцию y=f(x) к прямой y=kx+b, т.е. попытаемся подобрать k,b так, чтобы y=kx+b как можно лучше апроксимировать функцию y=f(x). В качестве прямой y=kx+b предлагается выбрать ту, на которую лучше всего «ложаться» экспериментальные точки. у1=kx1+b Þ Е21= (y1-(kx1+b))2 характеризует степень удалённости точки (х1,у1) от прямой y=kx+b Е22= (y2-(kx2+b))2 и т.д. Естественный критерий, характеризующий близость всей совокупности точек к прямой y=kx+b К=åni=1E2i. К=к(к,b) – функция двух переменных. Найдём такие к*,b*, которые минимизируют значение К. К(к,b)= åni=1(yi-(kxi+b))2 Необходимое условие экстремума. DК/Dк=0; DК/Db=0 DК/Dк=åni=12(yi-(kxi+b))(-хi)=0 kåni=1 хi2+båni=1 хi =åni=1 хi yi; DК/Db=åni=12(yi-(kxi+b))(-1)=0 åni=1 yi -kåni=1 хi-nb=0. íì kåni=1 хi2+båni=1 хi =åni=1 хi yi î kåni=1 хi+nb=åni=1 yi cистема двух линейных уравнений с двумя неизвестными к и b. 12. Выпуклые функции в Rn и их свойства. Отрезок в Rn с концами a, b Î Rn – это множество точек х (t)= (1-t) a + t b, где t произвольное число из промежутка [0; 1]. Отрезок с концами a, b обозначается [ a, b ]. Отрезок [ a, b ] совпадает с множеством точек в Rn, представимых в виде с = aа + bb, где a,b - произвольные неотрицательные числа такие, что a+b=1. Множество Р Ì Rn называется выпуклым, если вместе с любыми двумя точками a, bÎР оно содержит и весь отрезок [ a, b ]. Функция n переменных f (х), определенная на выпуклом множестве РÌRn, называется выпуклой, если для любых двух точек a, b Î Р и любых двух чисел a,bÎ[0; 1] таких, что a+b=1, выполняется неравенство f (aа + bb) ≤ a f (а) + b f (b) Для непрерывной функции, заданной на выпуклом множестве Р, следующие условия равносильны: 1) f выпукла;
Неравенство из пункта 4 называется неравенством Йесена. выпуклая функция наз. строго выпуклой, если неравенство f (aа + bb) ≤ a f (а) + b f (b) строгое при всех a, b из области определения функции и α,β ≥0 таких, что α+β=1. Функция f наз. (строго) вогнутой, если –f (строго) выпукла, т.е. f (aа + bb) ≥ a f (а) + b f (b) Линейная функция f(x)=(c,x)+c0 одновременно выпукла и вогнута, но не строго. Свойства выпуклых функций. 1. функция с выпуклой областью определения Р Ì Rn выпукла тогда и только тогда, когда выпукло множество Нf ={(х,у):хÎР, у≥ f (x)} (из Rn+1) называемое надграфиком функции f (x). 2. Если f (x) выпукла, то функция α f (x) выпукла при α>0 и вогнута при α<0. 3. Если f (x) выпукла на Р, то множество Uf (α)={х: f (x) ≤ α} выпукло при любом α. (обратное утверждение неверно). 4. Сумма любого числа выпуклых функций на множестве Р Ì Rn выпуклана Р, если при этом хотя бы одна из суммируемых функций строго выпукла, то вся сумма строго выпукла. 5. Пусть Р Ì Rn – выпуклое множество, и для каждого i=1,2,…k пусть l i(x) – линейная функция n переменных, а fi (t) – функция одной переменной, выпуклая на l i(Р). Тогда функция F(х)=f1 (l 1(x))+…+ fК (l К(x)) выпукла на Р. При этом, если все функции fi (t) строго выпуклы и любая точка однозначно определяется набором (l 1(а)+…+ l К(а)), то F(х) строго выпукла. 6. Пусть f выпукла на Р Ì Rn , а φ(t) – возрастающая выпуклая функция на множестве f (Р) ÌR, тогда F(х)= φ(f(x)) выпукла на Р. Если f (x) строго выпукла, то и F(х) строго выпукла. 7. Дифференциируемая функция f (x) выпукла на множестве Р Ì Rn тогда и только тогда, когда (grad f (a), b-a) ≤ f (b)- f (a) для любых a,bÎР 8. Пусть f (x) – функция, непрерывная на отрезке [ a, b ]ÌR и дважды дифференциируемая на (a, b). Для выпуклости функции f (x) на [ a, b ] необходимо и достаточно выполнение неравенства f˝ (x)≥0 для всех tÎ (a, b). Для строгой выпуклости f (x) добавляется условие f˝ (x)≠0 ни на одном интервале, содержащемся в (a, b). 9.
и составим матрицу C=Cij(X). Функция f (x) строго выпукла на множестве D, если в каждой точке хÎ D выполняются следующие неравенства
∆1=с11>0, …, ∆n=det c>0 Опр. 1). Суммой этих рядов наз ряд. Каждый член которого равен сумме соответствующих членов рядов (1) и (2). 2) Ряд, каждый член которого равен произведению соответствующего члена ряда (1) на одно и то же действительное число, наз произведением ряда на действительное число λ. Св-ва. 1)Если ряд (2) сходится, и его сумма равна S, тогда произведение этого ряда на действительное число также сходится, и его сумма будет равна λS. Док-во: Пусть Sk- частичная сумма ряда (2), sk - частичная сумма ряда λ в1+ λ в2+…+λ вк +…, ясно, что λ Sk = sk. Переходя к пределу, получим: Lim sk=lim λSk= λlimSk= λS(k→∞) 2)Если ряды (1) и (2) сходятся, и их суммы соответственно равны S, S’, то ряд из определения 1) (назовем его (3)) также сходится, а его сумма будет равна S+S’. Док-во: Qk=Sk+Tk, где Qk, Sk,Tk – сответственно частич суммы рядо (1), (2), (3). Переходя к пределу при k→∞, получаем, что сущ-т LimQk и Q=S+T 3)Если ряд сходится, то ряд, полученный из данного путем отбрасывания или приписывания конечного числа членов также сходится. Док-во: Рассмотрим, когда отбрасывают первые n членов. Оставшийся ряд аn+1 +аn+2+… наз остатком исходного ряда (1). Пусть Сn- сумма первых n членов, Sk -частичная сумма исх. Ряда,S’k - частичная сумма остатка, при k>n: Sk = Cn+S’k Если сущ-т предел lim Sk k→∞, то сущ-т и предел lim S’k и наоборот. В частности, выполняется равенство: S=S’+Cn 4)Если ряд (1) сходится, то сходится и любой ряд. Полученный из него группировкой слагаемых, причем суммы обоих рядов одинаковы. Необходимое усл-е сходимости. Теорема. Если ряд (1) сходится, то предел его общего члена при к →∞ равен 0. lim ak=0 Док-во. 1){Sk=a1+a2+…+ak {Sk-1=a1+a2+…+ak-1, значит ак=Sk-Sk-1 2)Поскольку ряд сходится, то lim Sk = S, k→∞ 3) k→∞: lim ak= lim Sk- lim Sk-1 = S- lim Sk-1= S-S=0 ((k-1)→∞) Следствие: если lim ak≠0 или не сущ-т, то ряд расходится. Сформулированный признак явл. необходимым усл-м и не явл достаточным, чтобы ряд сходился. Признаки сравнения Пусть заданы два положительных числовых ряда: u1 + u2 + … + un + = n=1S¥ un, un > 0 для " n v1 + v2 + … + vn + = n=1S¥ vn, vn > 0 для " n 1) Если "n Î N: un £ vn и ряд n=1S¥ vn – сходится, то и ряд n=1S¥ un – сходится. Если "n Î N: un £ vn и ряд n=1S¥ un – расходится, то и ряд n=1S¥ vn – расходится. 2) Если $ lim un/vn = k, то ряды либо одновременно сходятся, либо n ® ¥ k = const одновременно расходятся.
Признак сходимости Даламбера. Если n=1S¥ un – положительный ряд, для которого lim un+1/un = L, то n ® ¥ 1) при L < 1 ряд сходится 2) при L > 1 ряд расходится 3) при L = 1 необходимы дополнительные исследования.
Интегральный признак сходимости. Теорема. Пусть n=1S¥un - положительный ряд, для которого 1) un= f(n); 2) y = f(x) определена для " x ³ 1, непрерывна и возрастает, тогда ряд сходится, если сходится несобственный интеграл 1∫+¥f(x)dx, причем если он сходится, то n=1S¥ un = 1∫+¥f(x)dx Условно сходящиеся ряды. Ряд а1+а2+…+аn+… называется условно сходящимся, если он сходится, а ряд, составленный из модулей его членов, расходится. (теорема Римана. Если ряд сходится условно, то в результате перестаноски его членов можно получить ряд, имеющий любую сумму, а также расходящийся ряд.)
Степенные ряды. Опр. Выражение вида а0+а1х+а2х2+…+акхк+…, (*) где а0, а1,а2,… - некоторая числовая последовательность наз степенным рядом. а0,а1,а2,…- коэффициенты степенного ряда. Если х придавать числовые значения, то будем получать числ. Ряды, которые могут сходиться и расходиться. Множество Х, при которых ряд (*) сходится, называется областью сходимости. Теорема Абеля. 1)Если ряд (*) сходится в некоторой точке х0≠0, то этот ряд будет сходится и при всех х, удовлетворяющих условию: |х|<|х0|. 2)Если ряд (*) расходится в т. х1≠0, то этот ряд расходится при всех x: |х|>|х1|. Док-во.1). По усл степенной ряд а0+а1х0+а2х02+…+акх0к+…(**) сходится, поэтому акх0к →0, при к→∞. Значит, сходящаяся последовательность {акх0к} ограничена, т.е. сущ-т константа М такая, что |акх0к|<M для всех к=0,1,2… Рассмотрим |а0|+|а1х0|+|а2х02|+…+|акх0к|+….(***) Пусть |х|<|х0|, тогда |акхк|=|акх0к||х/х0|<М|х/х0|к, причем |х/х0|<1. Поэтому члены ряда (***) не превосходят соответствующих членов сходящегося ряда М+М|х/х0|+М|х/х0|2+…+М|х/х0|к+…- суммы бесконечно убывающей геометрической прогрессии. Поэтому ряд (***) сходится, а ряд (**) сходится абсолютно. 2)Предположим, что ряд(**) расходится при х=х1, но для некоторого х:| х |>х1 По первой части теоремы ряд (**) сходится абсолютно при х=х1, следовательно получили противоречие. Ряд Тейлора. Пусть ф-я f(x) определена в некоторой окрестности точки х=0 и имеет в этой точке произволдные всех порядков. Степенной ряд f(х0)+ (f’(х0)/1!)*(x-х0)+ (f’’(х0)/2!)*(x-х0)2+…+(f(n)(х0)/n!)*(x-х0)n+… называется рядом Тейлора с центром х0 джлдя ф-и f(x). Теорема. Если ф-я разлагается в некоторой окрестности т. х0 по степеням х-х0, то он явл рядом Тейлора с центром х0. Приложения степенных рядов. 1. Вычисление значений показательной ф-и: пусть х=Е(х)+q, где Е(х)-целая часть числа х, q- дробная его часть, тогда ех= еЕ(х)* еq, гденаходят с помомощью умножения, а – с помощью разложения ех=1+х+х2/2!+х3/3!+…+хn/n!+…. При 0≤х<1, этот ряд быстро сходится, поскольку остаток ряда Rn(x) оценивается след образом: 0≤ Rn(x) <хn+1/n!n 2. Вычисление значений логарифмической ф-и: Ln(1+x)= x- х2/2+х3/3-…+(-1)nхn+1/(n+1)+… Заменим х на –х: Ln(1-x)= -x- х2/2-х3/3-…+-хn+1/(n+1)-… вычитая из первого равенства второе получим: Ln(1+x)/(1-х)= 2(x+х3/3+х5/5+…), где |х|<1. 3. Вычисление значений синуса и косинуса: Sinx=x- х3/3!+х5/5!+…+(-1)nх2n+1/(2n+1)!+… Cosx=1- х2/2!+х4/4!+…+(-1)nх2n/(2n)!+… Ряды при больших х сходятся медленно. Но, учитывая периодичность ф-й синуса и косинуса и формулы приведения тригонометрич. Ф-й, достаточно уметь вычислять sinx, cosx для промежутка 0≤х ≤ π/4. 4. Разложение ф-й в степенные ряды исп-ся для приближенного нахождения интегралов, а также при решении дифференциальных уравнений.
Дифференциальные уравнения. Логический рост. Пусть р=р(у) – убывающая функция (dp/dy <0), т.е. с увеличением выпуска будет происходить насыщение рынка и цена будет падать. Проведя аналогичные рассуждения получим уравнение: y¢=kp(y)y,(здесь k=la.) уравнение представляет собой автономное дифференциальное уравнение. Так как k>0, p>0, y>0, то у(t) – возрастающая функция (y¢>0). Исследуем у(t) на выпуклость. Дифференцируя уравнение по t, получим y¢¢=ky¢(dp y +p) или y¢¢=ky¢p(dp * y +1), т.е. y¢¢=ky¢p(1- 1), dy dy p |ey| где ey(p)= dy * p - эластичность спроса. dp y Из этого вытекает, что если спрос эластичен, т.е. |ey|>1, то y¢¢>0, т.е. функция спроса – выпуклая функция. Если спрос неэластичен, т.е. |ey|<1, то y¢¢<0 и функция спроса – вогнутая функция. Пусть, например, р(у)=b-ay (a, b>0), тогда уравнение принимает вид: y¢=k(b-ay)y. Из чего легко получить, что y¢=0, если у=0 или у= b/a, а также, что у¢¢<0 при у= b/2a, и у¢¢>0 при у> b/2a. В данном случае легко получить и явное выражение для y(t). Разделяя переменные в уравнении, находим dy = kdt, или dy (1 + a)= kdt. y(b-ay) b у b-ay Проинтегрировав это соотношение, имеем Ln|y|-ln|b-ay|= kbt+lnC, т.е. y/(b-ay)=Cekbt. Отсюда получим y= Cekbt. 1+Caekbt График этой функции называется логистической кривой. Она также описывает некоторые модели распространения информации, динамику эпидемий, процессы размножения бактерий в ограниченной среде обитания и т.п. Из графика логистической кривой видно, что при малых t логистический рост схож с естественным ростом, однако при больших t характер роста меряется, темпы роста замедляются и кривая асимптоматически приближается к прямой у=b/a. Эта прямая является трационарным решением уравнения y¢=k(b-ay)y и соответственно случаю р(у)=0. Для этого уравнения также существуют решения при у> b/a, имеющие графики. Но так как в этом случае р(у)<0, то эти графики не имеют экономической интерпретации. Более реалистичной является модель, в которой скорость роста зависит не от дохода, а от прибыли. Пусть С(у)= aу+b - издержки (b,a - константы) тогда у¢=k(p(y)y-aу-b). Если p(y)=b-aу,то правая часть уравнения представляет собой квадратный многочлен относительно у с отрицательным коэффициентом перед у2. В этом случае возможны три варианта. 1) D<0. Следовательно, у¢<0. Издержки настолько велики, что это приводит к постоянному падению производства и в конце концов к банкротству. 2) D=0.В этом случае у¢ < 0 и меется одна стационарная кривая у=у* < b/a. При этом интегральные кривые, удовлетворяющие начальному условию у(t0)=y0>y*, будут ассимптотически приближаться к у* на +µ, а интегральные кривые, удовлетворяющие условию у(t0)< у* будут ассимптотически приближаться к у* на -µ. 3) D>0. В этом случае существует два стационарных решения у=у1, у=у2. (0<y1<y2). При этом у¢>0 при y1<у<y2 и у¢<0 при у<y1 или у>у2. 3. Неоклассическая модель роста. Пусть Y=F(K,L) – национальный доход, где К – обьём капиталовложений (фондов), L – величина затрат труда, F(K,L) – линейно-однородная производственная функция (F(tK,tL)=tF(K,L)). Пусть f(k) – производительность труда: F(k)= F(K,L)/L=F(K/L,1)=F(k,1), где k=K/L – фондовооружённость. Как известно, f¢(k)>0, f¢¢(k)<0. Предполагаем, что: 1. происходит естественный прирост трудовых ресурсов, т.е. L¢=aL(a=const); 2. Инвестиции направлены как на увеличение производственных фондов, так и на амортизацию, т.е. L¢=K¢+bK (b - норма амортизации).
Пусть l – норма инвестиций (т.е. I=lY), тогда lY=K¢+bK ÞK¢=lY-bK. Из определения фондовооружённости вытекает ln k=lnK-lnL. Дифференцируем эти соотношения по t, получим k¢/k=K¢/K-L¢L. Подставляя значения для L¢ и K¢, находим k¢ = lY-bK - a, т.е. k¢= lYk – (b+a)k = lYK -(b+a)k k K K kL Учитывая, что f=Y/L, получим K¢=lf(k)- (b+a)k. – уравнение неоклассического роста. Теория вероятностей. Комбинация событий. 1)Сумма событий А и В есть событие С, которое заключается в том, что либо А произошло, либо В, либо А и В произошли вместе. С=А+В 2)Произведение событий А и В есть событие Д, которое заключается в том, что А и В произошли вместе. Д=АВ 3)Противоположное событие. А – исходное событие, Ā – противоположное событие заключается в том, что А не произошло (напр, А – попадание при выстреле, Ā – промах). 4)Равенство между событиями. События А и В считаются равными, если всякий раз, когда наступает одно из них, наступает и другое.
Каждое событие можно истолковать как некоторое множество, а операции А+В, АВ, и Ā над событиями – как операции объединения, пересечения и дополнения для множеств. 5)А и В несовместны, если они не могут произойти вместе в одном опыте. АВ=Æ Геометрические вероятности
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.37.236 (0.018 с.) |

 2. Показательная. y=ax, a>0,a не равно 1. D(f)=R/ E(f)=(0;+¥). Если a>1, следовательно, функция возрастает. Если аÎ(0;1), функция убывает.
2. Показательная. y=ax, a>0,a не равно 1. D(f)=R/ E(f)=(0;+¥). Если a>1, следовательно, функция возрастает. Если аÎ(0;1), функция убывает.


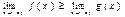 4.Если в некоторой окрестности точки х0 имеем f (x)≥g(x), то и если пределы существуют.
4.Если в некоторой окрестности точки х0 имеем f (x)≥g(x), то и если пределы существуют. 5. Если в некоторой окрестности точки х0 имеем f (x)≥g(x)≥h(x) причем пределы f (x) и h(x) при х→ х0 существуют и равны между собой
5. Если в некоторой окрестности точки х0 имеем f (x)≥g(x)≥h(x) причем пределы f (x) и h(x) при х→ х0 существуют и равны между собой Опр.Число а называют пределом функции f (x)в точке х0 справа, если для любой сходящейся к х0 последовательности {хn}, в которой все хn>х0, соответствующая последовательность {f(хn)} сходится к а.
Опр.Число а называют пределом функции f (x)в точке х0 справа, если для любой сходящейся к х0 последовательности {хn}, в которой все хn>х0, соответствующая последовательность {f(хn)} сходится к а.

 Прямая у=кх+b является наклонной асимптотой графика у= f (x) при х→+∞, если f (x) представима в виде f (x)= кх+b+α(х), где
Прямая у=кх+b является наклонной асимптотой графика у= f (x) при х→+∞, если f (x) представима в виде f (x)= кх+b+α(х), где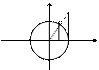
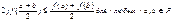


 Пусть D – выпуклое открытое множество в пространстве Rn, f (x)= f (x1,…,хn) – функция, имеющая в D непрерывные частные производные второго порядка. Для каждой точки хÎ D положим
Пусть D – выпуклое открытое множество в пространстве Rn, f (x)= f (x1,…,хn) – функция, имеющая в D непрерывные частные производные второго порядка. Для каждой точки хÎ D положим




