
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы существования решений системы функциональных уравнений.Содержание книги
Поиск на нашем сайте
Пусть m функций F1(х1,…, хn, u1,…, um); F2(х1,…, хn, u1,…, um); ……………………… Fm(х1,…, хn, u1,…, um)
F1(х1,…, хn, u1,…, um) = 0; F2(х1,…, хn, u1,…, um) = 0; ……………………… Fm(х1,…, хn, u1,…, um) = 0, Причем это решение непрерывно и дифференцируемо в указанной окрестности точки (х10,…, хn0). При этом ∂fk / ∂xj = - D(F1,…,Fm) / D(u1,…,uk-1, xj, uk+1,…, um): D(F1,…,Fm) / D(u1,…,um). Выражения для частных производных второго и последующих порядков, при условии их существования, можно получить посредством дифференцирования этих формул. Теоремы существования решений функционального уравнения. Пусть функция F(х1, х2,…, хn, u) непрерывна на области D евклидова пространства Rn+1, F(х10, х20,…, хn 0, u0) = 0; (∂F / ∂u) (х10, х20,…, хn 0, u0) ≠ 0 (точка (х10, х20,…, хn 0, u0) Î D). Тогда существует окрестность указанной точки, в которой уравнение F(х1,…, хn, u) = 0 однозначно разрешимо, причем решение u = f(х1, х2,…, хn) непрерывно в этой окрестности. Если, кроме условий, оговоренных выше, функция F дифференцируема в окрестности точки (х10, х20,…, хn 0, u0) и ∂F / ∂u непрерывна в этой точке, то решение u = f(х1, х2,…, хn) дифференцируемо в окрестности рассматриваемой точки, причем ∂f / ∂xk = - ∂F / ∂xk: ∂F / ∂u, k = 1,2,…,n. Частные производные второго и более высоких порядков, при условии их существования, могут быть найдены посредством дифференцирования формул для частных производных первого порядка.
Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Точка М0 называется точкой локального максимума (минимума) функции f(x,y), если существует такая окрестность точки М0, в которой для любой точки М(х,у) выполняется неравенство f(M)£f(M0) (f(M)³f(M0)). Точки локального экстремума называются просто точками экстремума. Необходимое условие существования экстремума. Если функция f(x,y) имеет частные производные первого порядка в точке локального экстремума М0(х0,у0), то f¢x(M0)=f¢y(M0)=0. Доказательство. Рассмотрим сначала функцию одной переменной f(x,y0). Производная этой функции совпадает с частной производной f¢x(x,y0), а сама функция имеет локальный экстремум в точке х0. Следовательно, производная функция f(x,y0) в точке х0 равна нулю, т.е. f¢х(x,y0)=0. Аналогично функция от одной переменной f(x,y0) имеет локальный экстремум в точке у=у0. Следовательно, её производная в этой точке равна нулю, т.е. f¢у(x,y0)=0. Равенство частных производных нулю выражает лишь необходимое, но не достаточное условие существования экстремум. Точки, в которых частные производные равны нулю или не существуют, называют критическими точками. Достаточное условие существования экстремума. Пусть функция f(x,y) имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки М0(x0,y0). Положим D= f¢¢xx(M0)f¢¢yy(M0) – (f¢¢xy(M0)2. тогда: 1. если D>0, то в точке М0 функция имеет локальный экстремум, причём f¢¢xx(M0)<0 – локальный максимум, при f¢¢xx(M0)>0 – локальный минимум; 2. если D<0, то в точке М0 нет экстремума. 3. если D=0, то требуются дополнительные исследования. (в лекциях 2-го семестра доказательства не приводилось, если есть большая тяга к знаниям, то см учебник стр 182-185).
Наибольшее и наименьшее значения функции на ограниченном замкнутом множестве. Схема исследования функции на экстремум. 1. z¢x, z¢y 2. Найти критические точки. z¢x=0, z¢y=0 3. Взять производные z¢¢xx,z¢¢yy,z¢¢xy,z¢¢yx. 4. C помощью условия существования экстремум сделать вывод. Теорема Вейерштрасса. Если функция z=f(x,y) непрерывна на замкнутом, ограниченном множестве, то на этом множестве функция принимает наибольшее и наименьшее значение.
Правило нахождения максимума и минимума для функции от двух переменных. 1. Найти ОДЗ и обедиться, что оно замкнутое и ограниченное. 2. Исследовать на экстремум, вычислить значение функции. 3. Вычислить значения функции на границах ОДЗ. 4. Из всех значений выбрать наибольшее и наименьшее. Метод наименьших квадратов. (рассмотрим для двух величин, остальные аналогично0Пусть (Х,У) – система двух случайных величин. Задача – исследовать связь между Х и У. М(У/Х=х) – условные математические ожидания случайной величины У при условии, что Х=х (х – фиксированное число) М(У/Х=х)=f(x). Уравнение y=f(x) называется уравнением регрессии СВ У на СВ Ч. Будем приближать функцию y=f(x) к прямой y=kx+b, т.е. попытаемся подобрать k,b так, чтобы y=kx+b как можно лучше апроксимировать функцию y=f(x). В качестве прямой y=kx+b предлагается выбрать ту, на которую лучше всего «ложаться» экспериментальные точки. у1=kx1+b Þ Е21= (y1-(kx1+b))2 характеризует степень удалённости точки (х1,у1) от прямой y=kx+b Е22= (y2-(kx2+b))2 и т.д. Естественный критерий, характеризующий близость всей совокупности точек к прямой y=kx+b К=åni=1E2i. К=к(к,b) – функция двух переменных. Найдём такие к*,b*, которые минимизируют значение К. К(к,b)= åni=1(yi-(kxi+b))2 Необходимое условие экстремума. DК/Dк=0; DК/Db=0 DК/Dк=åni=12(yi-(kxi+b))(-хi)=0 kåni=1 хi2+båni=1 хi =åni=1 хi yi; DК/Db=åni=12(yi-(kxi+b))(-1)=0 åni=1 yi -kåni=1 хi-nb=0. íì kåni=1 хi2+båni=1 хi =åni=1 хi yi î kåni=1 хi+nb=åni=1 yi cистема двух линейных уравнений с двумя неизвестными к и b. 12. Выпуклые функции в Rn и их свойства. Отрезок в Rn с концами a, b Î Rn – это множество точек х (t)= (1-t) a + t b, где t произвольное число из промежутка [0; 1]. Отрезок с концами a, b обозначается [ a, b ]. Отрезок [ a, b ] совпадает с множеством точек в Rn, представимых в виде с = aа + bb, где a,b - произвольные неотрицательные числа такие, что a+b=1. Множество Р Ì Rn называется выпуклым, если вместе с любыми двумя точками a, bÎР оно содержит и весь отрезок [ a, b ]. Функция n переменных f (х), определенная на выпуклом множестве РÌRn, называется выпуклой, если для любых двух точек a, b Î Р и любых двух чисел a,bÎ[0; 1] таких, что a+b=1, выполняется неравенство f (aа + bb) ≤ a f (а) + b f (b) Для непрерывной функции, заданной на выпуклом множестве Р, следующие условия равносильны: 1) f выпукла;
Неравенство из пункта 4 называется неравенством Йесена. выпуклая функция наз. строго выпуклой, если неравенство f (aа + bb) ≤ a f (а) + b f (b) строгое при всех a, b из области определения функции и α,β ≥0 таких, что α+β=1. Функция f наз. (строго) вогнутой, если –f (строго) выпукла, т.е. f (aа + bb) ≥ a f (а) + b f (b) Линейная функция f(x)=(c,x)+c0 одновременно выпукла и вогнута, но не строго. Свойства выпуклых функций. 1. функция с выпуклой областью определения Р Ì Rn выпукла тогда и только тогда, когда выпукло множество Нf ={(х,у):хÎР, у≥ f (x)} (из Rn+1) называемое надграфиком функции f (x). 2. Если f (x) выпукла, то функция α f (x) выпукла при α>0 и вогнута при α<0. 3. Если f (x) выпукла на Р, то множество Uf (α)={х: f (x) ≤ α} выпукло при любом α. (обратное утверждение неверно). 4. Сумма любого числа выпуклых функций на множестве Р Ì Rn выпуклана Р, если при этом хотя бы одна из суммируемых функций строго выпукла, то вся сумма строго выпукла. 5. Пусть Р Ì Rn – выпуклое множество, и для каждого i=1,2,…k пусть l i(x) – линейная функция n переменных, а fi (t) – функция одной переменной, выпуклая на l i(Р). Тогда функция F(х)=f1 (l 1(x))+…+ fК (l К(x)) выпукла на Р. При этом, если все функции fi (t) строго выпуклы и любая точка однозначно определяется набором (l 1(а)+…+ l К(а)), то F(х) строго выпукла. 6. Пусть f выпукла на Р Ì Rn , а φ(t) – возрастающая выпуклая функция на множестве f (Р) ÌR, тогда F(х)= φ(f(x)) выпукла на Р. Если f (x) строго выпукла, то и F(х) строго выпукла. 7. Дифференциируемая функция f (x) выпукла на множестве Р Ì Rn тогда и только тогда, когда (grad f (a), b-a) ≤ f (b)- f (a) для любых a,bÎР 8. Пусть f (x) – функция, непрерывная на отрезке [ a, b ]ÌR и дважды дифференциируемая на (a, b). Для выпуклости функции f (x) на [ a, b ] необходимо и достаточно выполнение неравенства f˝ (x)≥0 для всех tÎ (a, b). Для строгой выпуклости f (x) добавляется условие f˝ (x)≠0 ни на одном интервале, содержащемся в (a, b). 9.
и составим матрицу C=Cij(X). Функция f (x) строго выпукла на множестве D, если в каждой точке хÎ D выполняются следующие неравенства
∆1=с11>0, …, ∆n=det c>0
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.149 (0.009 с.) |

 Дифференцируемы в некоторой окрестности точки a = (х10,…, хn0, u10,…, um0) евклидова пространства Rn+m, причем частные производные этих функций по переменным u1,…, um непрерывны в точке a. Тогда если все функции F1,…,Fm обращаются в нуль в точке a, якобиан D(F1,…,Fm) / D(u1,…,um) отличен от нуля в этой точке, то найдется окрестность точки (х10, х20,…, хn0), в которой существует единственные m функции u1 = f1(х1, х2,…, хn), u2 = f2(х1, х2,…,хn), …, um = fm(х1, х2,…, хn), являющиеся решениями системы
Дифференцируемы в некоторой окрестности точки a = (х10,…, хn0, u10,…, um0) евклидова пространства Rn+m, причем частные производные этих функций по переменным u1,…, um непрерывны в точке a. Тогда если все функции F1,…,Fm обращаются в нуль в точке a, якобиан D(F1,…,Fm) / D(u1,…,um) отличен от нуля в этой точке, то найдется окрестность точки (х10, х20,…, хn0), в которой существует единственные m функции u1 = f1(х1, х2,…, хn), u2 = f2(х1, х2,…,хn), …, um = fm(х1, х2,…, хn), являющиеся решениями системы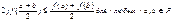


 Пусть D – выпуклое открытое множество в пространстве Rn, f (x)= f (x1,…,хn) – функция, имеющая в D непрерывные частные производные второго порядка. Для каждой точки хÎ D положим
Пусть D – выпуклое открытое множество в пространстве Rn, f (x)= f (x1,…,хn) – функция, имеющая в D непрерывные частные производные второго порядка. Для каждой точки хÎ D положим



