
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция F(x) называется первообразной для функции f(x) на интервале Х, если в каждой точке этого интервала выполняется условие F ` (x)=f(x). Например, для функции f(x) = 2х первообразной является F(х) = х2 для любых х Є (-∞, ∞). Действительно, F`(x) = 2x = f(x). F1(x) = x2 + 2 так же является первообразной для f(x) = 2x, F2(x) = x2 – 100 первообразная той же функции f(x) = 2x. Теорема. Если F1(x) и F2(x) первообразные для функции f(x) на некотором интервале Х, то найдется такое число С, что справедливо равенство: F2(x) = F1(x) + C, Или можно сказать так, две первообразные для одной и той же функции отличаются друг от друга на постоянное слагаемое. Определение. Совокупность всех первообразных для функции f(x) на интервале Х называется неопределенным интегралом от функции f(x) и обозначается
F(x) – некоторая первообразная для f(x), С – произвольная постоянная. Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Основные свойства неопределенного интеграла. 1. ( 2. Дифференциал от неопределенного интеграла равен подинтегральному выражению. d( 3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.
4. Постоянный множитель можно выносить за знак интеграла:
5. Интеграл от суммы двух функций равен сумме интегралов от этих функций
Для вычисления неопределенных интегралов от функций используют таблицу неопределенных интегралов, которая приводиться ниже. Таблица неопределенных интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Пример 1. Вычислить Решение. Воспользуемся свойствами 4 и 5 неопределенных интегралов и первой табличной формулой.
= 2(x2/2) – 3[(х3/2 *2)/3] – x + C = x2 - 2 Пример 2. = 2[(x1/2 *2)/1] – ln │x│ - 4 cosx +C = 4 Для вычисления неопределенных интегралов применяют следующие методы: метод непосредственного интегрирования, метод подстановки(метод замены переменной), метод интегрирования по частям. Существуют элементарные функции первообразные которых элементарными функциями не являются. По этой причине соответствующие неопределенные интегралы называются «неберущимися» в элементарных функциях, а сами функции не интегрируемыми в элементарных функциях. Например, Тема 13. Определенный интеграл, его свойства. Формула Ньютона - Лейбница. Понятие интегральной суммы. Пусть на отрезке [a, в] задана функция у = f(x). Разобьем отрезок на п элементарных отрезков точками деления а = х0, х1, х2, …, хп = в. На каждом элементарном отрезке [xi-1, xi] выберем произвольную точку Сi и положим
Эту сумму будем называть интегральной суммой для функции у=f(x) на отрезке [а, в]. Интегральная сумма зависит как от способа разбиения отрезка [a, в] на п частей так и от выбора точек С1, С2, …, Сп на каждом элементарном отрезке разбиения. Геометрический смысл интегральной суммы.
S1 S2 S3
0 а=х0 в1 х1 с2 х2 с3 х3 =в х Рис.1 Пусть п=3, тогда а = х0, х1, х2, х3=в. С1,С2,С3 точки, выбранные произвольно на каждом элементарном отрезке. S1 = f1(C1) ∆x1 – площадь прямоугольника, построенного на первом отрезке разбиения, ∆х1 = х1-х0, S2 = f2(C2) ∆x2 – площадь прямоугольника, построенного на втором отрезке разбиения. ∆х2 = х2-х1,
Это площадь ступенчатой фигуры, составленной из прямоугольников.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.20.13 (0.01 с.) |

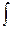 f(x)dx, где
f(x)dx, где  , где к - число
, где к - число 2-x2) = (arcsin x/a) + C
2-x2) = (arcsin x/a) + C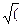 a2 +x2) = ln │x+
a2 +x2) = ln │x+  -1)dx.
-1)dx.





 Пусть у = f(x) неотрицательна на отрезке [а, в]. Рис.1
Пусть у = f(x) неотрицательна на отрезке [а, в]. Рис.1
 y = f(x)
y = f(x)

 у
у



