
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип неопределенности Гейзенберга.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В классической механике предполагалось, что координата точки и ее импульс могут быть определены одновременно с любой точностью. Попробуем понять, какие трудности возникают, если пытаться применить классические понятия к объекту, обладающему двойственной природой (частица-волна). Рассмотрим так
D р ® 0, а протяженность ее D х ® ¥. Очень узкий волновой пакет содержит множество волн, количество которых в пределе стремится к бесконечности и разброс импульсов в нем D р ® ¥ [13], а протяженность D х ® 0. Т.о., мы приходим к выводу, чем более точно локализован волновой пакет, тем больше оказывается неопределенность в его импульсе. Гейзенберг выдвинул принцип неопределенности: «Существует принципиальное ограничение на точность, с которой могут быть определены физические величины, не связанное с точностью приборов». Он предложил также формулы, смысл которых в следующем.
Существует также соотношение неопределенности, касающееся энергии и времени.
Из соотношений неопределенностей следует, что чем точнее определяется одна величина, тем менее точно – другая при одновременном их измерении,. Так как С помощью соотношений неопределенностей можно дать простые объяснения фактам, установленным другими путями. Например. 1). Входит ли электрон в состав атомного ядра?
2). Оценим с помощью соотношения неопределенностей энергию связи электрона в атоме водорода.
3). Найдем предел точности, с которой можно определить частоту и длину волны излучаемого света
Уравнение Шрёдингера. Открытие двойственной природы частиц привело к пониманию о невозможности описывать поведение микрочастиц с помощью классических представлений и законов. Стало ясно, что нельзя говорить о траектории частицы, т.е. о точном ее местоположении в любой момент времени. Появилась новая наука – квантовая механика. Вместо слова траектория частицы было введено понятие о вероятности нахождения частицы в том или ином месте пространства. Для описания поведения микрочастиц Шрёдингер (1926 г) предложил дифференциальное уравнение:
Математически уравнение Шрёдингера имеет бесконечное число решений, что физически неприемлемо, поэтому на пси-функцию накладываются дополнительные условия: 1).Пси-функция должна быть: а) конечной – вероятность не может быть больше 1, б) непрерывной – вероятность не может внезапно оборваться, в) однозначной – не может быть две вероятности в одной точке, 2) Производные пси-функции должны быть непрерывны, 3) Пси-функция должна подчиняться условию нормировки:
В тех случаях, когда потенциальная энергия зависит только от координат и не зависит от времени, т.е U = U (x,y,z), пси-функцию можно представить как произведение двух функций: Y (x,y,z,t) = y (x,y,z)× j (t). (Y - большая буква пси, y - малая буква пси, обе функции называются пси- или волновыми функциями.) Подставим в уравнение (i) и, разделим на (y × j).. Получим:
Если приравнять константе Е правую часть уравнения, получим:
При решении уравнения Шредингера мы
Решение уравнения с учетом дополнительных условий, накладываемых на пси-функцию, приводит не к любым величинам энергии Е, а к дискретным: Е1, Е2,…, Еn. В теории Бора электрон мог находиться тоже только в дискретных энергетических состояниях, но при этом была введена искусственно гипотеза о квантовании момента импульса электрона. Уравнение Шрёдингера приводит к квантованию энергии естественно, как математическое решение. При решении оказывается, что данному энергетическому состоянию частицы могут соответствовать одна или несколько (к) пси-функций. Иначе говоря, при данной энергии Еn частица может вести себя по-разному. Тогда говорят, что уровень Еn к -кратно вырожден и обозначают пси-функцию как
Рассмотрим подробнее пси-функцию.
Уравнение Шрёдингера (a) решается точно только для упрощенных, нереальных случаев, например, электрон в одномерной потенциальной яме. Из реальных объектов уравнение можно решить точно только для атома водорода при использовании сферических координат и для иона
ПРИМЕНЕНИЕ УРАВНЕНИЯ ШРЁДИНГЕРА Гармонический осциллятор. В классической физике гармоническим осциллятором называют частицу, совершающую движения по закону синуса или косинуса. Потенциальная энергия такой частицы U = кх2/2, частота колебаний
Мы не приводим решение этого уравнения, т.к. оно выходит далеко за рамки курса. [16] Из решения следует, что полная энергия Е такого осциллятора квантуется:
даже при абсолютном нуле (Т = 0 К) частица имеет энергию ¹ 0. На рис. показаны плотности вероятности
Существование нулевой энергии следует также из соотношения неопределенности. Действительно.
Таким образом, из соотношения неопределенностей следует, что энергия осциллятора равна
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 923; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.011 с.) |

 называемый пакет волн. Если сложить несколько волн с различными частотами, распространяющиеся в направлении х, получится сложная несинусоидальная волна [12]. Если будет складываться очень большое число волн со всевозможными длинами, образуется волновой пакет шириной D х (см.рис.). Монохроматическая волна имеет определенную длину волны и, соответственно импульс р = h / l = const,
называемый пакет волн. Если сложить несколько волн с различными частотами, распространяющиеся в направлении х, получится сложная несинусоидальная волна [12]. Если будет складываться очень большое число волн со всевозможными длинами, образуется волновой пакет шириной D х (см.рис.). Монохроматическая волна имеет определенную длину волны и, соответственно импульс р = h / l = const,

 очень мало, то эти ограничения существенны только в атомных масштабах.
очень мало, то эти ограничения существенны только в атомных масштабах.
 МэВ
МэВ
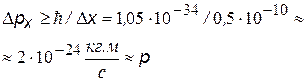
 эВ
эВ


 Гц
Гц

 i
i


 - набла (греч. слово nabla - арфа, символ по форме напоминает этот инструмент)
- набла (греч. слово nabla - арфа, символ по форме напоминает этот инструмент)

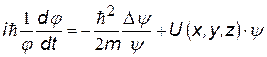



 a
a
 Если на систему воздействовать внешним, например магнитным полем, то вырождение снимается, уровень расщепляется на несколько уровней. Практически это обнаруживается в спектрах, вместо одной линии появляются несколько. Например, в спектре атома водорода на приборе с большим разрешением можно обнаружить, что почти все линии спектра являются дублетами.
Если на систему воздействовать внешним, например магнитным полем, то вырождение снимается, уровень расщепляется на несколько уровней. Практически это обнаруживается в спектрах, вместо одной линии появляются несколько. Например, в спектре атома водорода на приборе с большим разрешением можно обнаружить, что почти все линии спектра являются дублетами. 1/м3
для 3-х-мерного случая
1/м3
для 3-х-мерного случая
 1/м
для одномерного случая
1/м
для одномерного случая


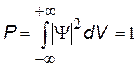
 в эллиптических координатах. Во всех остальных случаях для решения применяются приближенные методы.
в эллиптических координатах. Во всех остальных случаях для решения применяются приближенные методы.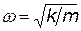 . Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.
. Посмотрим, к каким результатам приведет решение уравнения Шрёдингера (a), если его применить к одномерной частице, которая обладает такой потенциальной энергией.

 при
n = 0
при
n = 0
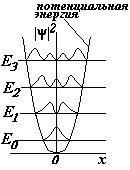 По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии;
По классическим представлениям при Т ® 0 К энергия должна стремиться к 0, решение уравнения Шрёдингера приводит к выводу о существовании нулевой энергии; при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.
при различных энергиях Е осциллятора. Если мы спросим себя, а как ведет себя частица, ведь нам всегда хочется наглядно представить процессы. Ответ – не знаем, ведь квантовый объект имеет двойственную природу. Мы можем только сказать, что частица находится в потенциальной яме, имеет определенный набор энергий и, если ее энергия равна, например Е1, то вероятность обнаружить ее в середине ямы равна нулю. При переходе на другой уровень энергия частицы меняется дискретно, и система поглощает или испускает порцию энергии hn.

 .
.


